Тема 9. Кривые второго порядка
Кривые второго порядка. Канонический вид кривой с центром в начале координат, со смещенным центром.
Нормальное уравнение окружности. Эллипс и его параметры. Координаты фокусов, эксцентриситет.
Уравнение гиперболы. Асимптоты гиперболы, координаты фокусов. Виды уравнений параболы. Директрисы, фокусы, параметр параболы.
Тема 10. Прямая, плоскость и поверхность в пространстве
Прямая в пространстве, ее виды. Канонические уравнения прямой в пространстве. Прямая, заданная пересечением плоскостей.
Плоскость в пространстве. Общее уравнение плоскости. Нормальное уравнение плоскости. Нормаль к плоскости. Плоскость, проходящая через точку, перпендикулярно заданному вектору.
Поверхности в пространстве. Эллипсоид, гиперболоид, параболоид, конус, цилиндр, шар.
ЛИТЕРАТУРА
Основная литература
1.Владимиров Ю.Н. Краткий курс по высшей математике. – М.: Окей-книга, 2010.
2.Ермаков В.И. Общий курс высшей математики для экономистов: Учебник (Гриф МО РФ). – М.: ИНФРА-М, 2010.
3.Кремер Н.Ш. Высшая математика для экономистов: Учебник. – 3-е изд. перераб. и доп. (Гриф МО РФ) / Под ред. Н.Ш. Кремер, Б.А. Путко, И.М. Тришин и др. – М.: Высшее образование, 2010.
4.Кремер Н.Ш. Высшая математика для экономистов: Практикум для студентов ВУЗов, обучающихся по экономическим специальностям. – 2-е изд., перераб. (Гриф МО РФ) / Под ред. Н.Ш. Кремер, Б.А. Путко, И.М. Тришин и др.– М.: ЮНИТИ-ДАНА, 2010.
5.Кремер Н.Ш. Математика для экономистов: от Арифметики до Эконометрики: Учеб.-справ. пособие / Под ред. Н.Ш. Кремер, Б.А. Путко, И.М. Тришин. – М.: Высшее образование, 2007.
6.Макарова С.И. Математика для экономистов. Задачник: Учеб.-практ. пособие (Гриф МО РФ) / С.И. Макарова, М.В. Мищенко. – М.: КноРус, 2008.
7.Солодовников А.С. Математика в экономике: Учебник для вузов. В 2 ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, А.Г. Шандра. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2008.
Дополнительная литература
8.Клименко Ю.И. Высшая математика для экономистов: теория, примеры, задачи: Учебник для вузов. – М.: Экзамен, 2005.
9.Клюшкин В.М. Высшая математика для экономистов: Учеб. пособие для вузов (Гриф МО РФ). – М.: ИНФРА-М., 2009.
5
10.Красс М.С. Чупрынов Б.П. Математика для экономистов (Гриф МО РФ). – СПб.: Питер, 2010.
11.Макаров С.И. Математика для экономистов [Электронный ресурс]: электронный учебник. - 2-е изд., стереотип. – М.: КноРус, 2009.
12.Плис А.А., Сливина Н.А. MATHCAD: математический практикум (Гриф МО РФ). – М.: Финансы и статистика, 2003.
Адреса сайтов в Интернете
•http://exponenta.ru/educat/class/class.asp (Internet-класс по высшей математике)
•http://mathelp.spb.ru/la.htm (Лекции по линейной алгебре)
•http://www.mathem.h1.ru/ (Математика On-Line)
•http://www.imamod.ru/magazin (Журнал «Математическое моделирование»)
•http://www.i-exam.ru (Интернет – тестирование)
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Тема 1. Матрицы и матричные операции
1. Для матриц:
p |
1 |
p |
|
|
|
|
−2 3 |
|
p |
|
|
|
p |
|
||||
|
|
|
|
|
|
1 |
|
|||||||||||
|
1 |
|
|
2 |
|
, |
|
|
|
|
|
|
1 |
|
|
и |
C = p2 |
|
A = |
0 |
p3 |
|
|
|
|
B = |
|
p3 |
0 |
|
|
||||||
|
−3 |
|
|
p2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.1. 4A – 3B + 6 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
−1 4 5 |
|
|
|
|
|
|
|
|
|
|
||
1.2. (AT B)T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.3. (AC )T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.4. AT A + BT B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
p |
2 |
и В = |
p |
p |
|
|
|
|||||
Для матриц А = |
1 |
|
|
2 |
3 |
вычислить функции: |
||||||||||||
|
|
|
|
|
|
1 |
p3 |
|
|
|
|
3 |
p1 |
|
|
|||
1.5. f (A), если |
f (x)= p x2 |
− p |
2 |
x + p . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
p |
0 |
(A+B) – |
p |
|
2 |
|
|
|
|
||||||
1.6. f (A, B) = |
|
3 |
|
|
|
1 |
|
BT. |
|
|
||||||||
|
|
|
3 |
1 |
|
|
2 |
p2 |
|
|
|
|
||||||
Литература: 1–6.
6
Тема 2. Определители квадратных матриц
1. Вычислить определители:
|
p1 |
p2 |
|
|
|
|
p1 |
p2 |
p3 |
|
||
|
|
|
|
|
|
|||||||
1.1. |
. |
|
|
1.2. |
1 |
2 |
0 |
|
|
. |
||
|
−4 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
1 |
4 |
|
|
|
Решить уравнения: |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||
|
x |
|
p2 |
|
= 6. |
|
1 |
0 |
−2 |
|
|
= p 2 . |
|
|
|
|
|
||||||||
|
|
|
|
|||||||||
1.3. |
|
|
1.4. |
x |
p |
p |
|
|
||||
|
p3 |
p1(x +1) |
|
|
|
|
2 |
3 |
|
|
1 |
|
|
|
|
|
3 |
4 |
p2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Литература: 1–6.
Тема 3. Обратная матрица
1. Проверить существование и вычислить обратные матрицы для следующих матриц:
p |
p |
|
|
|
1 |
p1 |
1.2. В = |
|
p |
−3 |
|||
1.1. А = 1 |
3 |
. |
|
|||
2 |
p2 |
|
|
3 |
|
|
|
|
|
p2 |
|||
|
|
|
|
p1 |
||
Литература: 1–6.
p2 p1 . p3
Теме 4. Матричные методы решения систем линейных уравнений
1. Решить системы линейных уравнений по формулам Крамера:
p1x − p2 y = 8 |
|
|
x |
+ x |
|
− p x = 6 |
. |
1.2. |
1 |
|
2 |
1 3 |
|
1.1. |
p2 x1 +3x2 −7x3 =16 . |
|||||
3x + p3 y =17 |
|
|
|
|
|
|
|
|
|
5x1 + p3x2 + x3 =16 |
|||
Решить системы уравнений методом обратной матрицы:
p1x1 + p3x2 |
= 8 |
|
|
x |
+ p x |
|
+ p x |
|
=1 |
||||||||
. |
1.4. |
|
1 |
|
1 |
2 |
|
|
2 |
3 |
|
|
|
||||
1.3. |
|
|
|
p3 x1 −3x2 + p1x3 = −2 . |
|||||||||||||
2x1 |
+ p2 x2 |
=12 |
|
|
p x |
+ p x |
2 |
+ p x |
3 |
= 4 |
|||||||
|
|
|
|
|
|
|
1 |
1 |
|
2 |
|
|
3 |
|
|
||
7
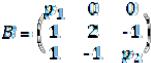
Решить матричные уравнения:
1.5. |
p |
p |
|
p |
−3 |
|
|
|
1 |
3 |
X = 2 |
−p |
. |
||
|
|
2 |
p |
|
p |
|
|
|
|
|
3 |
|
3 |
1 |
|
|
|
1 |
p1 |
1.6. Х |
p |
−3 |
|
|
|
3 |
|
|
|
|
p2 |
|
p1 |
||
p2 |
|
= (p |
|
|
p ) . |
p |
|
p |
2 |
||
1 |
|
1 |
|
3 |
|
p3 |
|
|
|
|
|
|
|
|
|
|
Литература: 1–6.
Тема 5. Векторы и векторные операции
1. Для векторов:
a1 |
p |
|
, |
a2 |
p |
|
|
, |
a3 |
2 |
|
решить задачи: |
||
= |
1 |
|
= |
|
2 |
|
= |
|
||||||
|
|
3 |
|
|
|
|
− |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
|||
1.1. p3a1 - p2 a3 + p1 a2 . |
|
|
|
|
|
|
|
|
||||||
1.2. a22 + ( a1 |
|
a2 ). |
|
|
|
|
|
|
|
|
|
|
||
1.3.Исследовать линейную зависимость векторов a1 и a2 .
1.4.Исследовать линейную зависимость векторов a1 , a2 и a3 .
1.5. Разложить вектор |
a2 |
|
1 |
|
p |
|
|
|
по базису из векторов |
− p |
|
и |
|
2 |
. |
||
|
|
|
|
|
1 |
|
||
|
|
|
1 |
|
|
|
|
|
Литература: 1–6, 8.
Тема 6. Линейные операторы
1. Найти собственные значения и векторы матрицы:
p |
p |
|
|
1.1. А= |
1 |
3 |
. |
|
2 |
p2 |
|
1.2.
Литература: 1–6.
8
Теме 7. Квадратичные формы
1. Определить, является ли квадратичная форма положительно определенной и привести ее к каноническому виду:
1.1.x2-4y2-2p1x+p3y
1.2.x2+2y2-p1x+p2y
Литература: 1–6.
Тема 8. Уравнение прямой на плоскости
1.Для прямой p1x + p2 y − p3 = 0 выполнить:
1.1.Привести общее уравнение к нормализованному виду и уравнению в «отрезках».
1.2.Определить расстояние от этой прямой до начала коорди-
нат.
1.3.Провести перпендикулярную ей прямую, проходящую через точку (20; –18) и записать ее уравнение.
1.4.Определить координаты точки пересечения данной прямой с
прямой
p22x − p1y + p3 = 0.
1.5. Определить уравнение прямой, проведенной через точки (p1; – p2) и (–2p1; p3).
Литература: 1–4, 7.
Тема 9. Кривые второго порядка
1. Построить кривые второго порядка. Привести уравнение к каноническому виду. Определить координаты центра, координаты фокусов.
1.1.p1 x2-p2 y2 –2p2y=0
1.2.p1 x2+p3 y2 +2p3х=4
Литература: 1–4, 7.
9
Тема 10. Прямая, плоскость и поверхность в пространстве
1.1.Построить уравнение прямой, проходящей через две данные точки и записать для нее каноническое уравнение и параметрические уравнения А(р1,0,р2), В(1,р3, 3).
1.2.Записать уравнение плоскости, проходящей через точки А, В, С(р2, 2, 5). Записать общее уравнение, нормальное, уравнение плоскости
вотрезках.
1.3.Построить поверхности
x2-4y2-2p1x+p2y+z=0 x2+2y2-p1x+4p2y-z2=0
Литература: 1–4, 7.
10
11
Битков Геннадий Николаевич Худякова Ольга Юрьевна
ЛИНЕЙНАЯ АЛГЕБРА
Программа курса. Практические задания
Редактор М.В. Егорова
Макет, верстка Т.А. Поверина Корректор Г.В. Платова
Лицензия ИД № 00871 от 25.01.00. Подписано в печать 11.10.2011
Формат 60×84 1/16. Усл. печ. л. 0,7. Изд. № 2259
Издательство МИЭП, типография МИЭП 105082 Москва, Рубцовская наб., д. 3, стр. 1
12