Тема 9. Кривые второго порядка.

Основные вопросы темы

1.Окружность: уравнение окружности и его основные параметры.

2.Эллипс: уравнение эллипса и его основные параметры.

3.Гипербола: уравнение гиперболы и его основные параметры.

4.Парабола: уравнение гиперболы и его основные параметры.

Кривые второго порядка на плоскости описываются уравнениями второй степени с двумя переменными. К ним относятся, в частности, окружность, эллипс, парабола и гипербола.

9.1 Окружность.

ОПРЕДЕЛЕНИЕ. Окружностью называется множество точек на плоскости, равноудаленных от заданной, называемой центром.

Рисунок 9.1. Окружность с центром в точке (х0 , у0).

Уравнение окружности, радиуса r, с центром в точке (х0 , у0) записывается как:

(x − x0 )2 + (y − y0 )2 = r2 .

В частности, окружность радиуса r, с с центром в начале координат описывается уравнением:

x2 + y2 = r2 .

ПРИМЕР. Показать, что уравнение

x2 + y2 – 6x – 8y – 96 = 0

является уравнением окружности, найти ее радиус и координаты центра.

Решение. Преобразуем заданное выражение, группируя отдельные его члены с целью выделения полных квадратов относительно переменных х и у:

57

x2 + y2 – 6x – 8y – 96 = (x2 – 2·3x + 9 – 9) + (y2 – 2·4y +16 – 16) – 96 = = (x – 3)2 – 9 + (y – 4)2 – 16 – 96 = (x – 3)2 + (y – 4)2 – 121 = 0.

Откуда:

(x – 3)2 + (y – 4)2 = 121,

или:

(x – 3)2 + (y – 4)2 = 112.

Данное уравнение описывает окружность, радиуса 11, с центром в точке (3, 4).

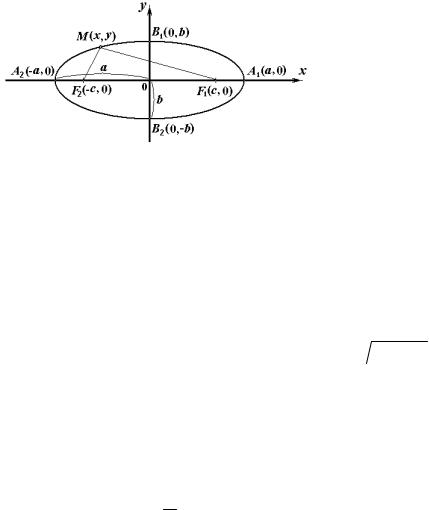
9.2 Эллипс.

ОПРЕДЕЛЕНИЕ. Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух заданных фиксированных точек, называемых фокусами, есть величина постоянная.

Рисунок 4.10. Эллипс.

Каноническое уравнение эллипса (оси эллипса совпадают с осями координат) имеет вид

где: параметры a и b задают размеры полуосей эллипса;

точки F1(c,0) и F2(-c, 0) определяют фокусы эллипса (при a > b); координата с фокуса определяется выражением: c = a2 − b2 .

Точки A1(a,0), A2(-a, 0), B1(0, b) и B2(0, -b) называются вершинами эллипса.

Форму эллипса (его вытянутость) характеризуют с помощью па-

раметра ε, называемого эксцентриситет эллипса:

ε = añ .

Значение эксцентриситета удовлетворяет соотношению: 0 ≤ ε ≤ 1 . При уменьшении значения эксцентриситета, расстояние между фокусами

58

уменьшается, а форма эллипса приближается к окружности. В пределе, при значении эксцентриситета равном нулю, форма эллипса полностью совпадает с окружностью.

Если центр эллипса О(х0, у0) не совпадает с началом координат, то его уравнение имеет вид:

(x − x0 )2 + (y − y0 )2 = 1.

a2 b2

ПРИМЕР. Показать, что уравнение

4x2 + 25y2 – 8x – 100y + 4 = 0

является уравнением эллипса и определить:

-координаты его центра;

-большую и малую оси;

-координаты фокусов эллипса;

-эксцентриситет.

Решение. Преобразуем заданное выражение, группируя отдельные его члены с целью выделения полных квадратов относительно пере-

менных х и у:

4x2 + 25y2 – 8x – 100y + 4 =

=4(x2 – 2·x + 1) – 4 + 25(y2 – 2·2y + 4) – 100 +4 =

=4(x – 1)2 + 25(y – 2)2 – 100 = 0 => 4(x – 1)2 + 25(y – 2)2 = 100.

Откуда:

Данное уравнение описывает эллипс с центром в точке (1, 2) и полуосями равными 5 и 2.

Найдем координаты фокусов эллипса и его эксцентриситет. Координата с фокусов F1(c,0) и F2(-c, 0) определяется выражением

c = a2 − b2 = 52 − 22 = 21 .

Таким образом F1 (c,0) = F1 ( 21,0) и F2 (−c,0) = F2 (− 21,0).

9.3 Гипербола.

ОПРЕДЕЛЕНИЕ. Гиперболой называется множество точек на плоскости, для каждой из которых модуль разности расстояний до двух

59

заданных фиксированных точек, называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы (оси гиперболы совпадают с осями координат) имеет вид:

где: параметры a и b задают действительной и мнимой полуосей гиперболы;

точки F1(c,0) и F2(-c, 0) определяют фокусы гиперболы (с > а); координата с фокуса определяется выражением: c = a2 + b2 .

Эксцентриситет гиперболы – ε определяется аналогично эксцентриситету эллипса:

ε = añ ,

однако, в случае гиперболы, его значение больше единицы: ε > 1. Вершины гиперболы имеют координаты:

A1(a, 0) и A2(-a, 0).

Выделяя значение переменной у из уравнения гиперболы, полу-

чим:

График этой функции имеет асимптоты y = kx + p с угловым коэффициентом k, равным:

Таким образом, асимптоты гиперболы определяются уравнениями:

y = ± ba x .

График гиперболы изображен на рисунке ниже.

60

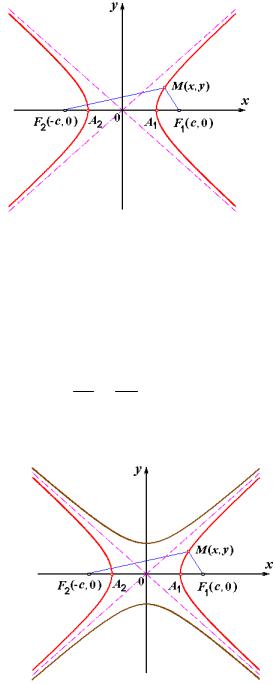
Рис. Гипербола. Отмечены фокусы F1(c,0) и F2(-c, 0) гиперболы и ее вершины A1(a, 0) и A2(-a, 0).

рассматривают, также, так называемую сопряженную (по отношению к исходной) гиперболу, определяемую уравнением:

x2 − y2 = −1. a2 b2

Ниже, на рисунке представлены обе гиперболы (исходная и сопря-

женная ей).

Рисунок 9.11. Исходная и сопряженная гиперболы.

ПРИМЕР. Показать, что уравнение

16x2 – 9y2 – 144 = 0

является уравнением гиперболы и определить:

-координаты ее вершин;

-координаты фокусов гиперболы; и

-эксцентриситет.

61

Решение. Преобразуем заданное выражение, разделив правую и левую часть на 144 и перенеся свободный член в правую часть уравнения:

Данное уравнение описывает гиперболу с параметрами a = 3 и b = 4. Вершины гиперболы имеют координаты: A1(a, 0) и A2(-a, 0). Подставляя найденные значения, получим: A1(4, 0) и A2(-4, 0).

Найдем координаты фокусов гиперболы и эксцентриситет. Координата с фокусов F1(c,0) и F2(-c, 0) определяется выражением

c = a2 + b2 = 32 + 42 = 25 = 5 .

Таким образом F1 (c, 0) = F1 (5, 0) и F2 (−c, 0) = F2 (− 5, 0).

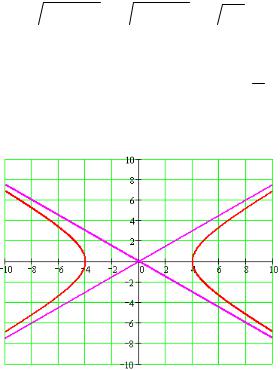
Найдем эксцентриситет ε гиперболы: ε = añ = 53 . Ее график (полученный с помощью пакета Mathcad) представлен на рисунке ниже.

9.4 Парабола.

ОПРЕДЕЛЕНИЕ. Параболой называется множество точек на плоскости, равноотстоящих от данной точки (фокуса и от данной прямой – директрисы.

Парабола задается уравнением:

(y − y0 )2 = 2 p(x − x0 ),

где: точка О(х0, у0) определяет вершину параболы;

62

р – параметр параболы. При р > 0 ветви параболы направлены вправо, при отрицательных значениях р – влево.

директрисой.

Каноническое уравнение параболы определяется как: y2 = 2 px ,

что соответствует случаю, когда вершина параболы совпадает с началом координат.

Рисунок 9.13. Парабола. Расстояние от фокуса до точки параболы равно расстоянию от этой точки до директрисы.

ЗАМЕЧАНИЕ. Если в уравнении параболы поменять местами переменные х и у, то получим уравнение:

x2 = 2 py ,

или

y = 21p x2 .

График этой функции представляет параболу, ветви которой направлены вверх (при р > 0), или вниз (при р < 0).

Рисунок 9.14. Парабола. Ветви направлены вверх при р > 0, или вниз (при р<0).

63