IvanovMaksyuta

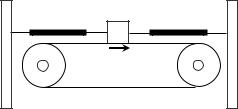
§ 4. Механічні системи з "від'ємним тертям"

Першим прикладом механічної системи з "від'ємним тертям" може слугувати пристрій, що зображений на рис. 6.

Рис. 6. Приклад механічної системи з від'ємним тертям

На стрічці, яка рівномірно рухається зі швидкістю v0 , лежить тіло з масою m , що закріплене двома пружинами з коефіцієнтами пружності k1 і k2 . Сила тертя між стрічкою та тілом є склад-

ною функцією відносної швидкості. Якщо позначити зміщення тіла через x , а його швидкість – через x , то силу тертя, яка діє на це тіло, можна вважати деякою функцією відносної швидкості (v0 − x) , тобто fT = f (v0 − x) . Якщо позначити сумарний

коефіцієнт пружності через k і вважати пропорційними першому степеню швидкості всі інші сили тертя (напр., опір повітря, внутрішнє тертя в пружинах тощо), то рівняння руху тіла масою m запишеться таким чином:

mx + bx + kx = f (v0 − x) .

Можна обмежити наш розгляд областю, у якій x << v0 (напр., обираючи велике значення v0 ). У цій області розкладаємо функцію f (v0 − x) у ряд в околі значення v0 й обмежуємось першими членами розкладу:

f (v0 − x) = f (v0 ) − xf ′(v0 ) +... ,

тобто прицьому обмеженні рівняння руху набуває такого вигляду:

61

Член f (v0 ) , що стоїть у правій частині цього рівняння, обумовлює лише зміщення стану рівноваги на величину f (v0 )k у напрямку руху стрічки. Величина і знак коефіцієнта b + f ′(v0 ) , що стоїть при x , залежать від вигляду характеристики тертя. Величина f ′(v0 ) є кутом нахилу характеристики тертя в точці v0 й у разі спадаючої характеристики тертя буде від'ємною f ′(v0 ) < 0 (рис. 1). Якщо характеристика тертя в околі v0 спадає достатньо круто, то може реалізуватися випадок, коли справедливою буде нерівність b + f ′(v0 ) < 0 . Тоді рівняння руху описуватиме систему з "від'ємним тертям".

і підшипником, на який підвішений маятник. Оскільки сила тертя залежить від відносної кутової швидкості (Ω0 −ϕ) вала й маятника, то момент сили тертя розкладаємо в ряд в околі значення Ω0 й обмежуємось першими членами розкладу:

f (Ω0 −ϕ) = f (Ω0 ) −ϕf ′(Ω0 ) +....

Оскільки член f (Ω0 ) викликає тільки зміщення положення рів-

новаги, кутову змінну можна відраховувати від цього нового зміщеного положення рівноваги. Рівняння ж руху набуває вигляду

62

Якщо буде справджуватися нерівність b + f ′(Ω) < 0 , то ми зно-

ву одержуємо механічну систему з "від'ємним тертям".

Таким чином, у цих двох прикладах особлива точка типу "центр" за малого тертя переходить в особливу точку типу "нестійкий фокус" (рис. 8, а), а у випадку сильного тертя переходить в особливу точку типу "нестійкий вузол" (рис. 8, б), на

якому нанесено пунктиром лінію x = λ1λ2 x(λ1 + λ2 ) , що про-

ходить через максимуми та мінімуми фазових траєкторій). Особлива ж точка типу "сідло" як за слабкого додатного і від'ємного тертя, так і при сильному додатному та від'ємному терті не змінює своєїприроди й залишається особливою точкою типу "сідло".

x x

x x

Рис. 8: a) oсоблива точка типу "нестійкий фокус"; б) oсоблива точка типу "нестійкий вузол"

Контрольні запитання та завдання

1.Залежність сили тертя від швидкості для сухих поверхонь.

2.Коли реалізується випадок слабкого (сильного) тертя?

3.У якому випадку виникає особлива точка типу "стійкий фокус"?

4.Уякомувипадкуреалізуєтьсяособливаточкатипу"нестійкийвузол"?

5.Приклади механічних систем, у яких "тертя" від'ємне.

63

Лекція 7. Вимушені коливання. Нелінійне тертя

§ 1. Метод Ван дер Поля. Знакозмінне тертя. Граничний цикл

Можна кількісно розглянути нелінійні системи, які будуть близькими до консервативних систем, зокрема, обмежимось випадком близьким до лінійних консервативних систем. Рівняння руху такої системи можна записати у вигляді рівняння другого

Тут μ – безрозмірний додатний параметр, який ми вважаємо ма-

лим (цей параметр визначає ступінь близькості нелінійної системи до лінійної консервативної).

Розглянемо, наприклад, рівняння руху другого порядку з функ-

яке описує лінійний осцилятор із частотою ω0 і з нелінійною та

знакозмінною силою тертя. Це рівняння називається рівнянням Ван дер Поля (або генератором Ван дер Поля). Якщо помножи-

ти це рівняння на mx , то його можна переписати у вигляді

тертям і особливою точкою буде особлива точка типу "нестійкий фокус", а за x > a навпаки, фазові траєкторії поводяться так, як у випадку особливої точки типу "стійкий фокус". Ці дві системи фазових траєкторій (пунктирні криві) асимптотично наближаються на фазовій площині до деякої особливої траєкторії (суцільна

64

крива), яку називають стійким граничним циклом (рис. 1, а). Якщо ж сили тертя мають вигляд fТ ( x, x) = μx(x2 a2 −1) , то виникає

нестійкий граничний цикл (рис. 1, б).

x

Рис. 1. Граничні цикли: а) стійкий, б) нестійкий

Знайдемо тепер рівняння фазової траєкторії граничного циклу, застосовуючи метод усереднення за часом, вважаючи при цьому коливання осцилятора швидким рухом, а зміну енергії в системі повільним рухом. Якщо візьмемо x = κcos ω0t , x = −κω0 sin ω0t ,

то, вимагаючи виконання такої рівності:

одержуємо κ = 2a , тобто траєкторією граничного циклу є еліпс, який перетинає вісь x у точках x1,2 = ±2a .

§ 2. Вимушені коливання

Нехай зовнішня сила змінюється за періодичним законом F (t) = f cos γt . У цьому випадку, як і за наявності тертя, енергія

не зберігається. Однак задачу вже не можна проаналізувати за допомогою методу фазової площини, оскільки в ній явно присутній час. У цьому випадку аналіз значно більш складніший, і його проведення виходить за межі даного курсу лекцій. Винятком є лінійний випадок, коли рівняння руху записується у вигляді

65

x + 2λx + ω02 x = mf cos γt .

Розв'язок зручно шукати, якщо переписати це рівняння в комплексній формі, а саме:

x + 2λx + ω02 x = mf exp (iγt) .

Частинний розв'язок шукаємо у вигляді x (t) = B exp (iγt) , оскільки

цього вимагає вигляд сили. Підставляючи його в комплексне рівняння, одержуємо

B = ( f ) = bexp (iδ) , m ω02 − γ2 + 2iλγ

де b = f m (ω02 − γ2 )2 + 4λ2γ2 , tg δ = 2λγ(γ2 −ω02 ) . Нехай

λ < ω0 . Тоді загальний розв'язок дійсного рівняння руху запису-

ється у вигляді

x (t) = a exp (−λt)cos (ωt + α) + bcos(γt + δ) .

Перший доданок у цьому виразі спадає за експоненціальним законом. Томучерезвеликийпроміжокчасузалишаєтьсялишедругий доданок, який не залежить від початкових умов, оскільки всі рухи такого осцилятора, навіть, якщо вони відрізняються початковими значеннями x і x , приводятьдоодногоасимптотичногостану.

Амплітуда вимушених коливань максимальна на частоті γ = ω02 − 2λ2 ≡ γm , що випливає з рівняння

На рис. 2 зображена залежність амплітуди b(γ) від частоти

ливань при наближенні частоти змушувальної сили до частоти власних коливань системи називається резонансом.

Розглянемо область поблизу резонансу за умови λ << ω0 . У цьому випадку виконується рівність

γm = ω02 − 2λ2 ≈ ω0 (1 −λ2ω02 ) = ω0 −λ2ω0 ≈ ω0 ,

тобто можна покласти γ = ω0 + ε, де ε – мала величина. Тоді,

враховуючи наближення

γ2 −ω02 = (γ −ω0 )(γ + ω0 ) ≈ 2ω0ε, 2iλγ ≈ 2iλω0 ,

но, що різниця фаз між коливанням і силою, що спонукає це коливання, завжди від'ємна, тобто коливання запізнюється щодо зовнішньої сили (рис. 3).

Зміна δ від нуля до −π відбувається у вузькій смузі частот ~ λ в околі ω0 . За відсутності тертя зміна фази вимушеного коливання відбувається стрибкоподібно за γ = ω0 . У стані динаміч-

ної рівноваги, коли система здійснює вимушені коливання, її енергія залишається незмінною за рахунок балансу в системі між неперервним поглинанням енергії від джерела зовнішньої сили та процесом її дисипації внаслідок наявності тертя. Усереднюючи швидкість зміни енергії

67

E = −2λmx2 = −2λmγ2b2 (γ)sin2 (γt + δ)

за часом, одержуємо кількість енергії I (γ) , що поглинається в середньому в одиницю часу, тобто маємо

оскільки γ ≈ ω0 . Такий вигляд залежності поглинання від частоти називається лоренцевим (рис. 4).

I (ε)I (0)

12

ε

−λ λ

Рис. 4. Залежність поглинальної потужності від частоти

Півшириною резонансної кривої на рис. 4 називається значен-

ня ε , за яким величина I (ε) зменшується в два рази порівняно

з її максимальним значенням Imax = I (0) = f 2 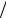4mλ за ε = 0 . Із залежності I (ε) випливає, що ця півширина дорівнює показни-

ку згасання λ . Висота ж максимуму I (0) = f 2 4mλ обернено

пропорційна λ . Таким чином, при зменшенні показника згасання резонансна крива стає вужчою і вищою, але площа при цьому не змінюється. Дійсно,

тобто за умови λ → 0 одержуємо

I (γ − ω0 ) → (πf 2 4m) δ(γ − ω0 ) ,

де δ( x) – дельта-функція Дірака.

68

§ 3. Катастрофа резонансу

Для коливань, що не згасають (за λ = 0 ) амплітуда b згідно з одержаною вище формулою прямує до нескінченності, коли частота γ прямує до ω0 . Рівняння руху в цьому випадку можна

записати таким чином:

x +ω02 x = mf sin γt ,

а його частинний розв'язок записується у вигляді xч (t ) = − m(γ2 f−ω02 )sin γt .

Об'єднуючи цей розв'язок із розв'язком x0 (t ) = Acos ω0t + Bsin ω0t однорідного рівняння, одержуємо за початкових умов x (0) = x0 , x (0) = 0 розв'язок рівняння руху

При наближенні частоти γ до частоти власних коливань ω0 одержуємо

Дійсно, використовуючи правило Лопіталя, обчислюємо x (t) за умови γ → ω0 :

Оскільки залежність від часу лінійна, то з часом величина x (t) необмежено зростає, тобто рух стає неперіодичним. У цьому – суть катастрофи резонансу.

69

З'ясуємо ще, як поводять себе коливання поблизу резонансу, коли γ = ω0 + ε, де ε – мала величина. Беремо розв'язок у комплексній формі

2πω0 , а тому рух поблизу резонансу можна розглядати як малі коливання, алезізмінноюамплітудою. ПозначаючиїїчерезС, маємо

С = A + B exp(iεt ) .

Використовуючи позначення A = a exp(iα) , B = bexp (iβ) , одержуємо:

C2 = a cos α+ bcos (εt +β) +ia sin α+ibsin (εt +β) 2 =

= a2 +b2 + 2abcos(εt +β−α).

Таким чином, розв'язок можна записати як коливання з амплітудою, яка періодично з частотою ε змінюється між двома

граничними значеннями a −b ≤ C ≤ a + b . Це явище називається явищем биття (на рис. 5 наведено залежність x (t) ).

x (t )

a +b a −b

t

− a −b

−a −b

Рис. 5. Ілюстрація явища биття

Рівняння руху може бути зінтегроване і в загальному випадку за довільної змушувальної сили F (t) , якщо це рівняння

70