IvanovMaksyuta

U (q)

E = U (qmax ) = Umax

q

qmin qmax

q

q

Рис. 8. Схематичне зображення фазових траєкторій у загальному випадку

З'ясуємо тепер на прикладі декартових координат поведінку фазових траєкторій поблизу точок повороту, а також визначимо характер руху на сепаратрисі. Запишемо рівняння траєкторії поблизу якої-небудь точки повороту

Розкладемо U (q) в околі точки повороту qi й обмежимося першими двома членами розкладу

U (q) =U (qi ) + ∂U∂(qqi ) (q − qi ) +... ≈ E + ∂U∂(qqi ) (q − qi ) .

51

Таким чином, поблизу точок повороту фазові траєкторії мають такі кореневі особливості: q (q − q1 )1/ 2 , q (q2 − q)1/ 2 ,

q (q − q3 )1/ 2 . Рух на сепаратрисі аперіодичний, оскільки за умови E →Umax період руху τ(E ) прямує до нескінченності. Очевидно, що це прямування до нескінченності відбувається за логарифмічним законом, оскількиза U (q) ≈Umax + κ2 (q − qmax )2 іза q → qmax :

Контрольні запитання та завдання

1.Який рух називається одновимірним?

2.Приклади механічних систем з одним ступенем вільності.

3.Як розраховується частота малих коливань?

4.Де розташовуються особливі точки на фазовій площині?

5.Означення сепаратриси та її рівняння.

52

Розділ ІІ ЛІНІЙНІ ТА НЕЛІНІЙНІ КОЛИВАННЯ

ЗА НАЯВНОСТІ СИЛ ТЕРТЯ

Лекція 6. Одновимірний рух матеріальної точки за наявності сил тертя

§ 1. Сили тертя та їх види

На рух тіла в середовищі діють сили опору. Енергія рухомого тіла при цьому переходить у тепло, тобто відбувається процес дисипації. Таким чином, рух за цих умов уже не є суто механічним, тобто потребує врахування руху самого середовища та внутрішнього теплового стану як середовища, так і тіла. Рівняння ж руху уже не будуть інваріантними щодо заміни t → −t . Прискорення тіла є функцією уже не тільки координат і швидкостей у даний момент часу, тобто не існує рівнянь руху в тому сенсі, який вони мають у механіці.

Проте існують такі умови, коли рух у середовищі може бути наближено описаний за допомогою механічних рівнянь шляхом введення в них деяких додаткових членів. Сюди належать коливання із частотами, малими порівняно з частотами, характерними для внутрішніх дисипативних процесів у середовищі. За виконання цих умов можна вважати, що на тіло, окрім сили

F ( x) = −∂U ( x)∂x , діє ще сила тертя fТ ( x) , яка залежить лише від швидкості тіла, тобто рівняння руху матиме вигляд mx = −∂U∂x + fТ ( x) . Для сили в'язкого тертя характерна ліній-

на залежність щодо швидкості, fT = −αvG. Можливі й більш

складні залежності. Наприклад, залежність сили тертя від швидкості для сухої поверхні зображена схематично на рис. 1.

53

За малих швидкостей сила тертя круто спадає майже за лінійним законом (це той інтервал швидкостей, за яких можливо реалізувати режим з "від'ємним тертям"). У випадках великих швидкостей маємо звичайний режим з

v "додатним тертям". Як у ви- падку "додатного тертя", так і у випадку "від'ємного тертя" спостерігаються режими

слабкого та сильного тертя (це визначається співвідношенням між параметрами механічної системи та характеристиками сил тертя). Окрім того, існують системи зі знакозмінним тертям.

§ 2. Лінійний осцилятор за наявності сили тертя

Допустимо, що сила тертя пропорційна швидкості. Зрозуміло, що таке припущення являє собою деяку ідеалізацію, а саме,

– ідеалізацію реальних законів тертя. Проте будь-який інший закон тертя порушував би лінійність осцилятора. Таким чином, узагальнену силу тертя fТ , що діє на систему, яка, у свою чергу,

здійснює одновимірні малі коливання з узагальненою координатою х, записуємо у вигляді

fТ = −bx ,

де b – додатній коефіцієнт, а знак мінус показує, що сила тертя діє в бік, протилежний швидкості х. Тоді рівняння руху лінійного осцилятора за наявності сили тертя записується у вигляді

mx + bx + kx = 0 .

Розділивши його на масу m і використовуючи позначення km = ω02 , bm = 2λ , де ω0 – частота вільних коливань системи за відсутності тертя, λ – коефіцієнт згасання, одержуємо

x + 2λx + ω02 x = 0 .

Розв'язок цього рівняння записується в такому вигляді:

54

x (t) = C1 exp (r1t) +C2 exp (r2t) ,

де r1 , r2 – корені квадратного рівняння r2 + 2λr + ω02 = 0 , а саме, r1,2 = −λ ± λ2 −ω02 . За λ2 < ω02 (випадок слабкого тертя) одержуємо згасаючий осциляторний процес, а за λ2 > ω02 (випадок

сильного згасання) одержуємо згасаючий аперіодичний процес. Розглянемо спочатку згасаючий осциляторний процес. По-

значаючи ω2 = ω02 −λ2 , дістаємо розв'язок у вигляді x (t) = exp (−λt)( Acos ωt + Bsin ωt) ,

де А і В визначаються початковими умовами. Наприклад, за

між двома послідовними проходженнями системи через положення рівноваги постійні та дорівнюють Т = 2πω . Такий самий

інтервал у часі буде і між двома послідовними максимумами. Цей проміжок часу будемо називати умовним періодом. Залеж-

ність x (t) зображена на рис. 2.

Швидкість згасання осциляторного процесу характеризується величиною λ . Але можна дати й іншу, кращу, характеристику згасання такого процесу, яка не залежить від вибору одиниць вимірювання. Розглянемо відношення двох послідовних максимумів

Логарифм цього відношення має назву логарифмічного декремента згасання d , причому d = Tλ . Обернена величина 1d дає кількість умовних періодів, після яких амплітуда зменшується в е разів

( A(t) = a exp (−λt) , A(t ) A(t +Tn) = exp (λTn) = e, n =1Tλ =1d ).

Видно, що одержаний закон згасання коливань тісно пов'язаний із прийнятим нами ідеалізованим законом тертя. Тільки припустивши, що сила тертя пропорційна швидкості, ми одержуємо закон спадання максимумів згідно з геометричною прогресією зі

знаменником прогресії exp (−d ) . Таким чином, згасаючі коли-

вання характеризуються чотирма величинами: умовним періодом (або умовною частотою), логарифмічним декрементом згасання, амплітудою та фазою.

x(t)

t

x1max x2 max

Рис. 2. Згасаючий осциляторний процес

Повна енергія системи визначається за формулою

значення повної енергії в початковий момент часу. Похідна за часом від повної енергії визначається таким чином:

56

Загальний вигляд розв'язку у цьому випадку є таким: x (t) = C1 exp (−λ1t) +C2 exp (−λ2t) .

Видно, що функція x (t) асимптотично (за t → ∞ ) наближається

до нуля (до рівноваги). Цей тип руху називається аперіодичним згасанням. Характер цього руху задається початковими умова-

1

2

3

t

4

Рис. 3. Характеристики аперіодичного згасання за таких початкових умов:

x0 > 0 ; 1 – x0 > 0 , 2 – x0 = 0 , 3 −λ2 x0 ≤ x0 < 0 , 4 – x0 < −λ2 x0

57

Нарешті, коли λ = ω0 , маємо r = −λ і загальний розв'язок у цьому випадку матиме вигляд x (t) = (C1 +C2t) exp(−λt) . Це

особливий випадок аперіодичного згасання. Він також не має коливального характеру, а його характеристики визначаються початковими умовами й аналогічні характеристикам, зображеним на рис. 3.

Вираз для сили тертя можна записати у вигляді похідної за швидкістю x від деякої функції F , яка називається дисипативною функцією. Для розглядуваного випадку

fТ = − ∂∂F = −bx , x

тобто дисипативна функція буде F = bx22 . Сила тертя має бути додана до правої частини рівняння Лагранжа

Дисипативна функція визначає інтенсивність дисипації в системі, оскільки згідно з dEdt = −bx2 маємо dEdt = −2F .

§ 3. Зображення згасаючих процесів на фазовій площині за "додатного тертя"

Перейдемо тепер до дослідження фазової площини системи, тобто до побудови її "фазового портрета", що відображає всю сукупність можливих рухів. Почнемо з випадку слабкого тертя, коли λ < ω0 . Тоді, розв'язуючи систему параметричних рівнянь

щодо невідомих exp(−λt )cos ωt і exp(−λt )sin ωt , а потім виключаючи час, можемо побудувати фазові траєкторії x = x( x) на основі такого трансцендентного рівняння:

58

Проте, якщо будемо розглядати дуже мале тертя, тобто λ << ω0 , то експоненту exp (−λt) можна вважати сталою при диференціюванні за часом. Тоді, використовуючи x (t) = a exp (−λt)cos (ωt + α) , одержуємо таку систему параметричних рівнянь траєкторій:

тобто на фазовій площині ( x, x) ми маємо сукупність логариф-

мічних спіралей, для яких початок координат є асимптотичною точкою. На рис. 4 зображені дві з таких траєкторій.

x

x

Рис. 4. Особлива точка типу "стійкий фокус"

Таким чином, особлива точка типу "центр" за малого тертя переходить в особливу точку типу "стійкий фокус".

59

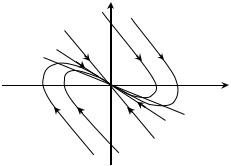
Розглянемо тепер випадок сильного тертя, коли λ > ω0 . У цьому випадку фазові траєкторії x = x( x) шукаємо з такої сис-

теми параметричних рівнянь:

x(t ) = C1 exp(−λ1t ) +C2 exp(−λ2t ) ,

x(t ) = −λ1C1 exp (−λ1t ) −λ2C2 exp(−λ2t ) ,

де C1,2 = (λ2,1x0 + x0 )(λ2 −λ1 ) . Дійсно, розв'язуючи щодо невідомих exp(−λ1t ) і exp (−λ2t ) і виключаючи час, ці траєкторії можна одержати з такого трансцендентного рівняння:

Знайдемо тепер асимптотики цих траєкторій за t → ±∞ . Оскільки λ1 < λ2 , то за t → −∞ другі доданки швидше прямують до нескінченності, ніж перші, тобто можна покласти С1 = 0 , і тоді маємо таку асимптотику: x = −λ2 x . За t → +∞ асимптотикою буде пряма x = −λ1x . На рис. 5 зображений фазовий портрет у цьому ви-

падку сильного тертя. У цьому випадку особлива точка типу "центр" переходить в особливу точку типу "стійкий вузол". Криві сукупності мають вертикальні дотичні (паралельні осі x ) у точках перетину з віссю x , а також мають горизонтальні дотичні (пара-

лельні осі x ) у точках перетину з прямою x = −λ1λ2 x(λ1 + λ2 ) .

x

x

Рис. 5. Особлива точка типу "стійкий вузол"

60