1. 4. Програма Advanced Grapher.

Advanced Grapher – це потужна, але легка в використанні програма для побудови графіків, креслення кривих і обчислення функцій. Вона дозволяє працювати в декартовій системі координат, будувати параметричні функції, графіки, рівняння. Можливості обрахунків: нулі і екстремуми функцій, перетин, похідні, рівняння нормалей, числове інтегрування (рис.1.1.)

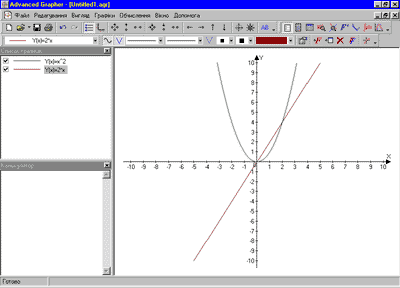
Рис.1.1

Використаня Advanced Grapher дозволить навчити учнів установлювати взаємозв`язок графіка функції та її властивостей – неперервність, точки розриву, проміжки зростання та спадання, знакосталості, опуклості, найбільше та найменше значення, точки максимуму, мінімуму, перегину, використовуючи для цього математичний апарат похідної і границь функції.

1. 5. Етапи створення посібника

Дослідивши поняття „електронного підручника” та ознайомившись з вимогами до нього ми створили власний посібник з курсу математичного аналізу. Він містить в собі теоретичний матеріал та практичні завдання, розроблені у відповідності з чинними програмою та підручниками з математичного аналізу.

Посібник має наступну структуру (рис.1.2.)

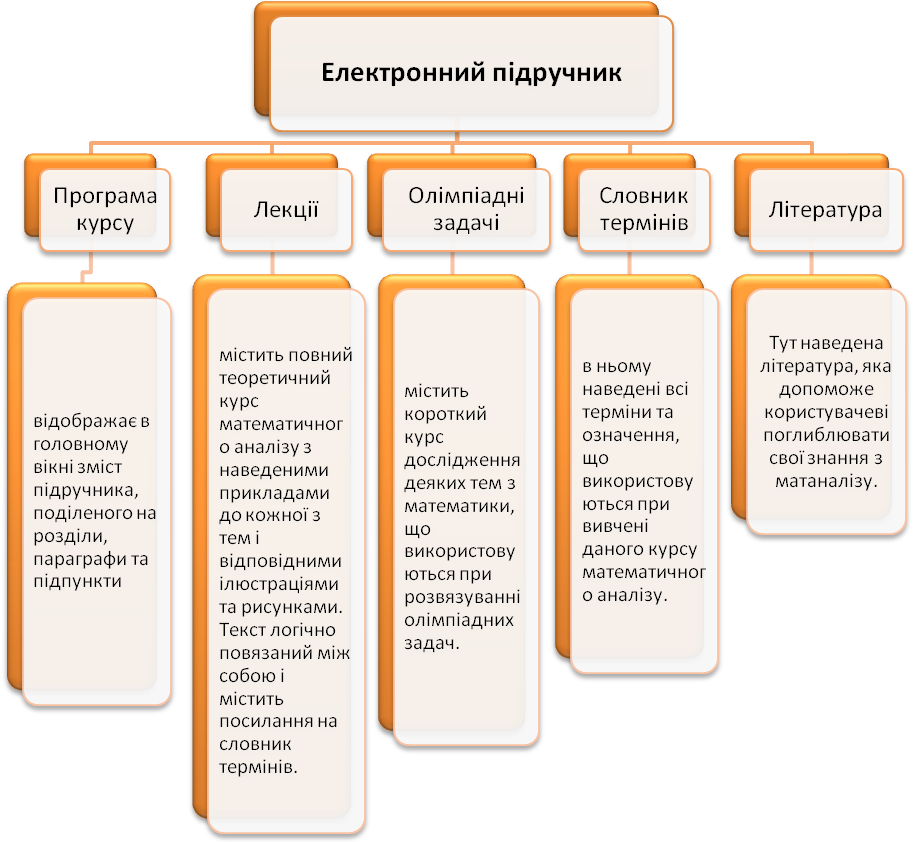
Рис. 1.2.

На 1-му етапі нашої роботи було розглянуто концепцію елек­трон­ного підручника, проаналізовано доцільність використання електронних під­руч­ників у навчальному процесі. До недоліків традиційних підручників віднесено: не­можливість зміни без перевидання (досить дорогого), практична неможливість  їх пристосування до індивідуалізації навчання кожного учня. Відповідно, пере­ва­га­ми електронних підручників є можливість багаторазової зміни і тиражування без ве­ликих матеріальних затрат, можливість настроювання для окремих користу­ва­чів, що дає змогу реалізувати принцип диференційованості навчання. Суттєвою пе­ре­вагою є можливість включати в них сучасні (у тому числі мультимедійні) спо­со­би представлення інформації, використовувати  інтерактивні засоби контролю знань, у тому числі і самоперевірки. Він забезпечує самостійність вивчення курсу, доступність до будь-якого розділу, зручність у використанні.

Наступним етапом був відбір матеріалу, його структурування за розділами, параграфами, підпунктами, складання змістів. Далі ми створили електронні версії теоретичного та практичного матеріалу за допомогою редактора Microsoft Word 2007. Основна робота проводилася в формульному редакторі, використовувались засоби для створення малюків, таблиць. Кожен підпункт розміщений в окремому файлі, які в свою чергу розміщені в загальному каталозі, що поділений на підкаталоги.

Для коректного відображення в браузері ми перетворили текстовий формат документу в HTML-формат. Редагуючи текст, створювали гіперпосиланням зовнішні (на термінологічний словник) та внутрішні, що встановлювали зв’язки між окремими поняттями та означеннями в тексті.

Електронний підручник складається з обкладинки, яка містить назву, перелік авторів та кнопку переходу на сам посібник (рис.1.3).

Рис. 1.3.

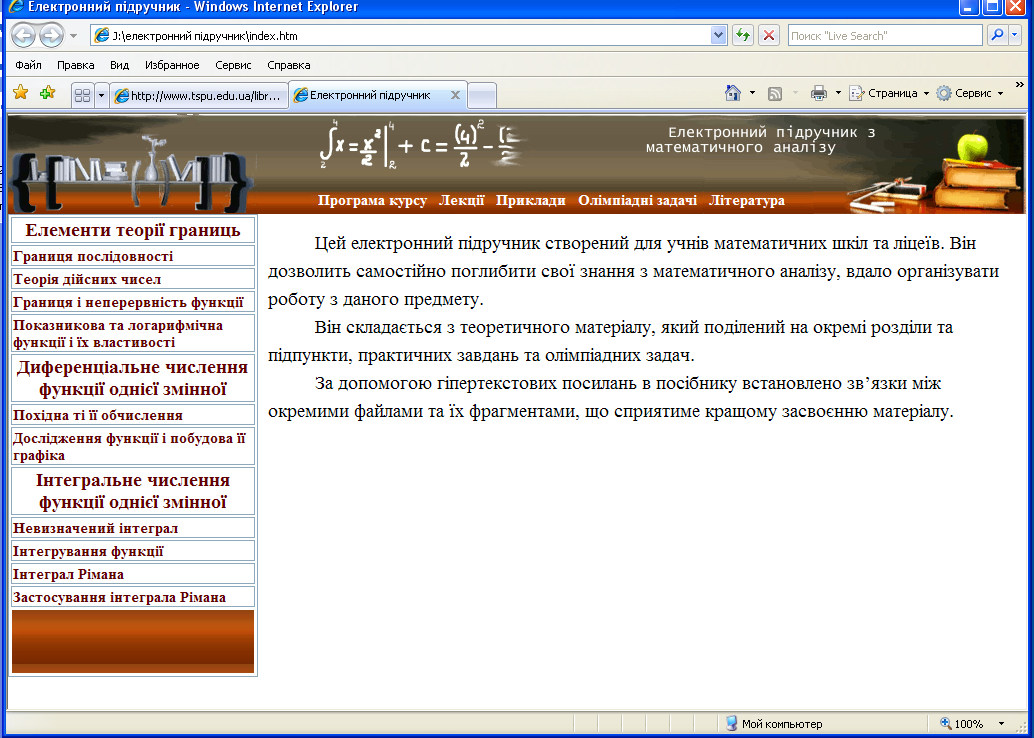
Рис. 1.4.

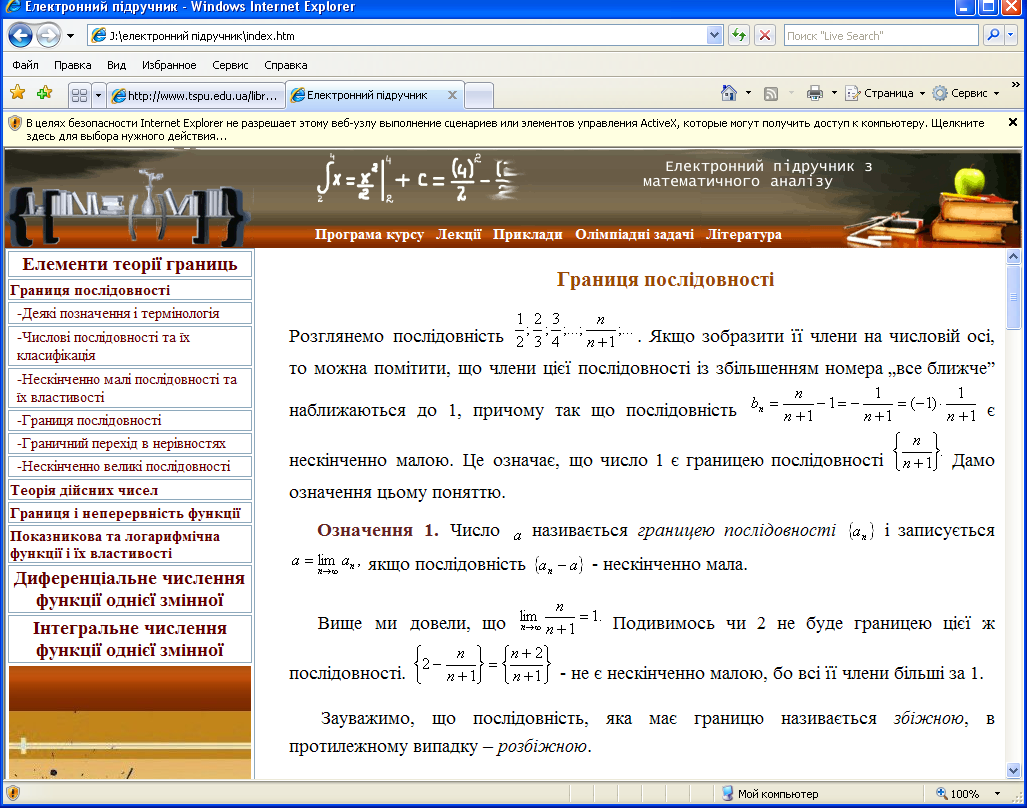
Рис. 1.5.

Він, в свою чергу містить три вікна (фрейми): верхній, лівий, головний

(рис. 1.4. – 1.5). Верхній фрейм містить графічні зображення (створені в програмі Photoshop) та навігаційне меню. Для коректного відображення малюнку в різних браузерах ми використали масштабування в відсотковому відношенні. За допомогою кнопок меню користувач має змогу викликати підменю у лівому вікні: зміст лекцій, курс по олімпіад них задачах, літературу. Використовуючи вже лівий фрейм, при наведенні клацанні мишею на назві потрібного розділу чи параграфу відбувається гіперпосиланням і у головному фреймі з’являється потрібний матеріал.

Таким чином наш програмний продукт є засобом забезпечення структурного, ґрунтовного, свідомого вивчення курсу математичного аналізу. Він на належному рівні забезпечить міцність засвоєння матеріалу, задовольнить цікавість здібного учня (адже містить нестандартні завдання), допоможе надолужити матеріал, якщо він по тій чи іншій причині не був вивчений. Підручник може бути роздрукований необхідним тиражем, що допоможе чергувати різні форми роботи для ефективного засвоєння ти вироблення навичок і вмінь. Викладач в свою чергу може змінювати, редагувати, вносити корективи в теоретичний та практичний матеріал. Усі бажаючі, хто є користувачем ПК можуть ознайомитися з нашою роботою та використовувати її в навчальних цілях.

В наступній частині магістерської роботи подається друкований варіант теоретичного матеріалу із наведеними прикладами задач та розділ „Олімпіадні задачі”, який містить створений електронний підручник.

РОЗДІЛ ІІ. ЕЛЕМЕНТИ ТЕОРІЇ ГРАНИЦЬ