2. 3. 5. Арифметичні операції над неперервними функціями

Теорема 1. Нехай і - функції визначені на множині і неперервні в точці Тоді неперервними в цій точці будуть функції:

Доведення. Візьмемо Тоді із неперервності і в точці матимемо (за означенням Гейне): і Розглянемо послідовність Для неї матимемо, А це за означенням Гейне і означає, що функція є неперервною в точці

В кінці попереднього параграфа ми довели, що

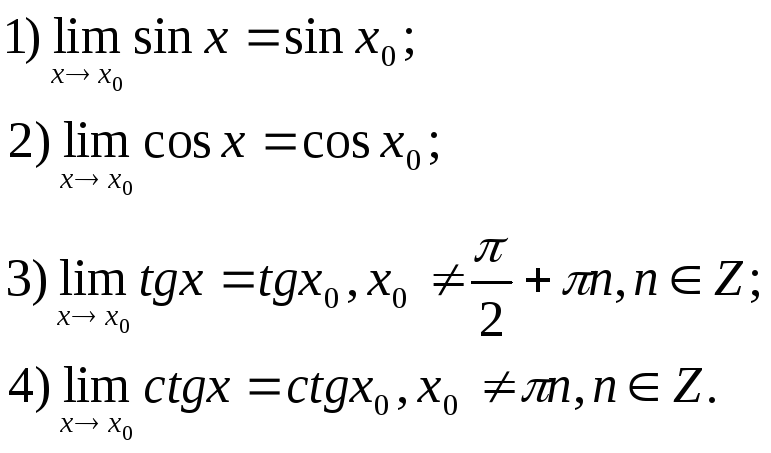
Перші дві рівності означають, що і неперервні в кожній точці числової осі. Третє означає, що неперервна функція всюди, де останнє означає, що неперервна всюди, крім Безпосередньо з означення неперервності і теорем про границі функції випливає, що будь-який многочлен є неперервною функцією на всій числовій осі, дробово-раціональна функція ( і - многочлени) – теж є неперервною функцією всюди, де

Нехай маємо функцію яка визначена на множині і - її множина значень. На множині визначена ще одна функція з множиною значень При цих умовах ми одержали на множині функцію з множиною значень яку називатимемо складною функцією, або композицією функцій і З’ясуємо при яких умовах складна функція буде неперервною.

Теорема 2 (про неперервність складної функції). Якщо функція неперервна в точці і функція неперервна в точці то складна функція - неперервна в точці

Доведення. Візьмемо довільну послідовність Звідси і з того, що - неперервна в точці за означенням Гейне неперервності функції матимемо, що послідовність Оскільки неперервна в точці то за означенням Гейне матимемо або, що те саме А це означає (за означенням Гейне), що функція неперервна в точці Теорема доведена.

Одностороння неперервність функції в точці

Нехай дана функція область визначення її, і точка така, що в будь-якому її лівому півоколі є безліч елементів множини Тоді можна говорити про Якщо то функція неперервна в точці зліва. Аналогічно вводиться і неперервність справа.

Очевидно справедлива наступна

Теорема 3. Якщо функція така, що можна говорити про її неперервність і зліва і справа в деякій точці, то для того, щоб функція була неперервна в цій точці необхідно і достатньо, щоб вона була неперервна в цій точці і зліва, і справа.

2. 3. 6. Властивості неперервних функцій

1. Локальна властивість

Теорема 1 (Про консервативність функції). Якщо функція неперервна в точці і то існує окіл точки такий, що

Доведення. Нехай для конкретності Візьмемо Оскільки функція неперервна в точці то за означенням Коші неперервності матимемо, що: або

або,

Випадок коли розглядається аналогічно.

Легко доводиться і наступна

Теорема 2. Якщо функція неперервна в точці то вона обмежена в деякому околі цієї точки.

Доведення пропонуємо провести самостійно.

2. Глобальні властивості

Функція називається неперервною на множині якщо вона неперервна в кожній точці цієї множини.

Наприклад. Функція є неперервною на а функція не є неперервною на

Наступним нашим завданням буде вивчення властивостей функцій неперервних на відрізку.

Теорема 3 (Веєрштрасса). Якщо функція неперервна на відрізку то вона обмежена на цьому відрізку.

Доведення. Те, що функція обмежена на означає

(1)

Доведемо цю теорему методом від супротивного. Припустимо, що (1) невірне. Тоді будемо мати,

(2)

Звідси отримаємо: (тут ми беремо в якості )

(3)

Із (3) одержуємо деяку послідовність всі члени якої належать відрізку а тому послідовність обмежена. Тоді за теоремою Больцано-Веєрштрасса існує збіжна підпослідовність тобто Оскільки то за теоремами про граничний перехід в нерівностях одержимо, що З умови теореми маємо, що функція неперервна в точці Тому з означення Гейне неперервності функції матимемо, що А оскільки ця послідовність збіжна, то вона і обмежена. Але ж із нерівності (3) будемо мати, що

(4)

Оскільки послідовність взята із означення підпослідовності, то Значить, як випливає з нерівності (4) послідовність є нескінченно-великою, а значить необмеженою, в той час як вище ми показали її обмеженість. Протиріччя! Тому припущення невірне і теорема доведена.

Зауваження. Ясно, що ця теорема перестає бути вірною, якщо відрізок замінити інтервалом або півінтервалом.

Спробуйте привести приклад неперервної на інтервалі функції, яка обмеженою на ньому не буде.

Попередньою теоремою ми показали, що при її умовах множина значень функції є обмеженою, а значить як ми знаємо існує і цієї множини, які ми позначатимемо так: і Наступна теорема відповідає на питання: чи досягаються ці числа нашою функцією на відрізку тобто чи існують точки

Якщо функція неперервна на інтервалі то очевидно і Легко бачити, що і 1 нашою функцією на інтервалі не досягаються. Проте має місце наступна

Теорема 4 (Веєрштрасса). Якщо функція неперервна на відрізку то існують точки ,

(а значить будуть відповідно найбільшим і найменшим значенням цієї функції на відрізку що будемо позначати так: ).

Доведення. (Приклад перед формулюванням теореми показує, що вона точна в тому розумінні, що в ній відрізок не може бути замінений на інтервал чи півінтервал.) Позначимо тоді Припустимо, що немає такої точки щоб Значить матимемо, що Розглянемо функцію Очевидно, ця функція неперервна (і невід’ємна) на відрізку Звідси за теоремою 1 матимемо:

Отже, Остання нерівність означає, що - нижня межа множини значень функції яка більша за яке є найбільшою з нижніх меж. Протиріччя! Припущення невірне. Значить і в цій частині теорема 2 доведена. Інша частина теореми доводиться аналогічно.

В елементарній математиці ми часто користуємося відомим методом інтервалів. Наступна теорема не тільки обґрунтовує цей метод, а має дуже багато інших різноманітних застосувань.

Теорема 5 (Больцано-Коші). Якщо функція неперервна на і на кінцях цього відрізка приймає значення різних знаків, то

Доведення. Нехай для конкретності і Позначимо через множину тих точок відрізка , де . Оскільки неперервна в точці (в цій точці вона неперервна справа), то за теоремою про консервативність існує . Значить

Аналогічно з тієї ж теореми одержимо множину таку, що а отже ні одна точка цього півоколу не належить до множини значить кожна із точок півоколу включаючи і , буде верхньою межею множини . Значить ми вже встановили (з використанням відомої теореми): - бо ми довели, що

Доведемо, що Припустимо, що це не так. Тобто Нехай Тоді за теоремою про консервативність Звідси маємо, що ні одна точка цього околу не належить до множини . Оскільки - верхня межа множини то ні одне і теж не належить до множини Значить маємо, що кожна точка буде верхнею межею множини в тому числі і Але ж це неможливо, бо - найменша з верхніх меж. Отримали протиріччя. Отже неправда, що

Випадок розглядається аналогічно. Отже і теорема доведена.

Теорема 6 (Больцано-Коші). Якщо функція неперервна на відрізку і то для будь-якого що лежить між числами і існує

Доведення. Нехай для конкретності і Ясно, що неперервна на Далі Тоді задовольняє всім умовам першої теореми Больцано-Коші, згідно з якою Звідси Теорема доведена.

Використовуючи доведені теореми можна вирішити проблему множини значень неперервної на відрізку функції.

Теорема 7 (про множину значень неперервної на відрізку функції). Якщо функція неперервна на відрізку то множиною її значень буде деякий відрізок або одноточкова множина.

Доведення. Якщо на відрізку то тоді ця константа і буде тією єдиною точкою з якої складатиметься множина значень цієї функції. Нехай тоді за другою теоремою Вейєрштрасса знайдуться: Очевидно, що Покажемо, що відрізок - множина значень на відрізку Візьмемо довільне Застосувавши ІІ теорему Больцано-Коші до функції на відрізку з кінцями і одержимо, що на цьому відрізку, а значить і на відрізку знайдеться Отже ми бачимо, що всі точки відрізка досягаються нашою функцією, тому він буде множиною значень цієї функції. Теорема доведена.

Очевидно теорема обернена до тільки-що доведеної (якщо множиною значень заданої на відрізку функції є відрізок, то неперервна на області визначення) є не вірною. Пропонуємо читачу підібрати відповідний приклад, що це підтверджує.

Теорема 8 (достатня умова неперервної функції). Якщо функція монотонно-зростаюча (спадна) на відрізку і відрізок є її множиною значень, то - неперервна на відрізку

Доведення. Нехай монотонно-спадна на відрізку і - її множина значень. Візьмемо Очевидно, що Тоді можна взяти настільки малим, щоб Тоді числа який за умовою є множиною значень нашої функції і тому ці числа досягаються нею на відрізку Значить З монотонного спадання нашої функції маємо, що Позначимо через Тоді а це означає, що тому неперервна в точці Якщо або то доведення аналогічне і пропонуємо його провести самостійно. Теорема доведена.

Ця теорема буде справедливою і для випадку не строго монотонних функцій. Щоб закінчити проблему неперервності монотонної функції ми доведемо теорему з якої випливатиме які точки розриву може мати монотонна на відрізку функція.

Теорема 9. Якщо функція монотонно неспадна (незростаюча) на відрізку то в точці існує правостороння границя, в точці - лівостороння, а існують обидві (скінченні) односторонні границі.

Доведення. Для доведення достатньо довести, що в точці існує скінченна правостороння границя, а в точці існує скінченна лівостороння границя. Візьмемо, що функція монотонно неспадна на відрізку і доведемо перший випадок:

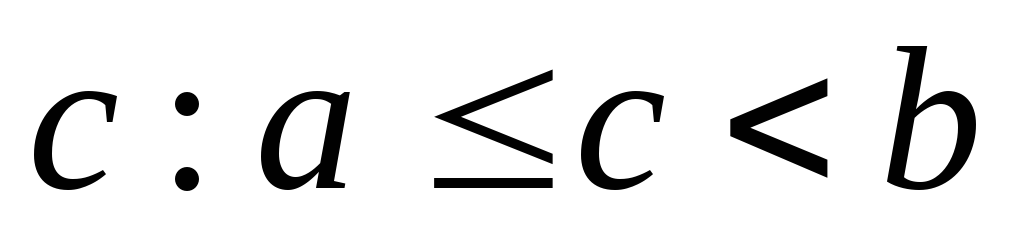1. в точці існує скінченна правостороння границя функції

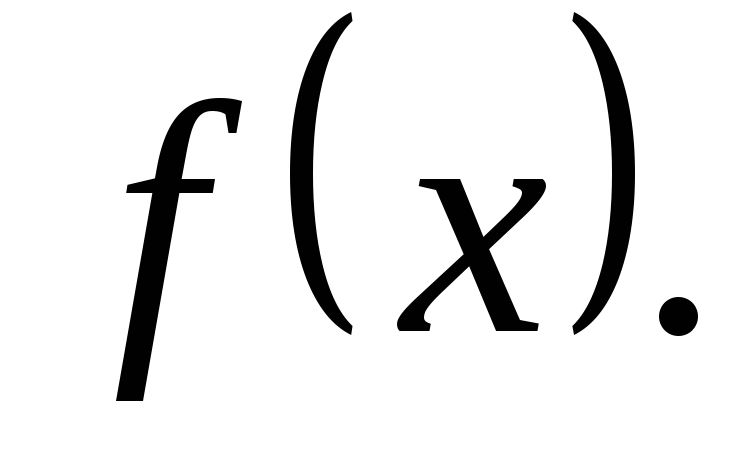
Для доведення позначимо через множину значень функції які вона приймає на півінтервалі Очевидно, що не порожня, бо Ясно, що обмежена знизу числом тому що Отже - нижня межа множини Тому за відомою теоремою випливає, що існує Ясно, що Покажемо, що одержане число буде дорівнювати Беремо За другою властивістю інфінууму матимемо, (а значить ): Оскільки то число Розглянемо далі інтервал Очевидно, що матимемо: Отже ми отримали: (1).

Оскільки то і оскільки то Звідси і з (1) маємо, а тому і теорема в цьому випадку доведена. Всі інші випадки розглядаються аналогічно. Врахувавши, що а - нижня межа множини будемо мати, Розглянувши другий випадок ми одержали б таку нерівність, а, значить, ми довели ще й таке: якщо функція - монотонно неспадна на відрізку то Зокрема з останніх нерівностей випливає: монотонна на відрізку функція не може мати на цьому відрізку усувних розривів (бо тоді було б ) і розривів ІІ роду (всюди існують односторонні границі!).

Отже, ми встановили істинність такого твердження.

Теорема 10 (про точку розриву монотонної функції). Якщо функція монотонна на відрізку , то на цьому відрізку вона не може мати ні усувних розривів, ні розривів ІІ роду.