4. 4. 2. Площа криволінійного сектора.

(Аналог криволінійної трапеції, але в полярних координатах)

Крім прямокутної декартової системи координат широко використовується в математиці і її застосування – так звана полярна система координат. Вона задається променем і точкою.

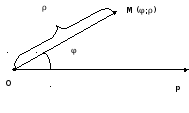
Точка називається полюсом, а промінь – полярною віссю. Візьмемо будь-яку точку . Нарисуємо промінь . Першою координатою буде кут , другою – довжина променя. Ясно, що будь-яка точка , за винятком початку координат, задана цими двома координатами. Що стосується точки , то вона першої координати не має. Неважко знайти зв’язок між полярними і декартовими координатами. Для цього початок декартової системи координат помістимо в точку . Вісь направимо по полярній осі.

З трикутника маємо:

Якщо, наприклад, ми візьмемо коло в декартовій системі координат, яке задається рівнянням , то в полярних координатах воно матиме такий вигляд : Коли в полярній системі координат ми маємо деяку криву, яка має ту властивість, що кожен промінь, який виходить з початку координат перетинає її не більше як в одній точці, то .

Нехай в полярній системі координат маємо фігуру, яка обмежена променями і і графіком функції , яка неперервна на . Потрібно знайти площу фігури, яку ми назвемо криволінійним сектором. Для розв’язання цієї задачі ми, як і раніше, поступимо наступним чином. Візьмемо довільне розбиття відрізка :

Під кутами проведемо промені. Візьмемо той елементарний криволінійний сектор, який лежить між променями . Знову з точки під кутом проведемо промінь. Тоді радіусом закреслимо дугу, кінці якої лежать на . Отримали круговий сектор з центром в точці , радіусом і розхилом . Знайдемо площу цього кругового сектора.

; .

Тоді площа всього криволінійного сектора приблизно дорівнюватиме:

Для того, щоб отримати вищу точність отриманого наближення треба зменшувати крок розбиття. А щоб отримати абсолютну точність треба перейти до границі коли . Тому логічно дати таке означення

Означення 1. Під площею криволінійного сектора ми будемо розуміти границю коли суми

(якщо звичайно вона існує).

Оскільки остання сума є інтегральною для функції на відрізку , то для ця сума є на неперервною, а значить інтегрованою за Ріманом. То згадана в останньому означенні границя існує і дорівнює

.

Таким чином ми встановили наступне:

1. Наш криволінійний сектор має площу;

2. Вона обчислюється за формулою

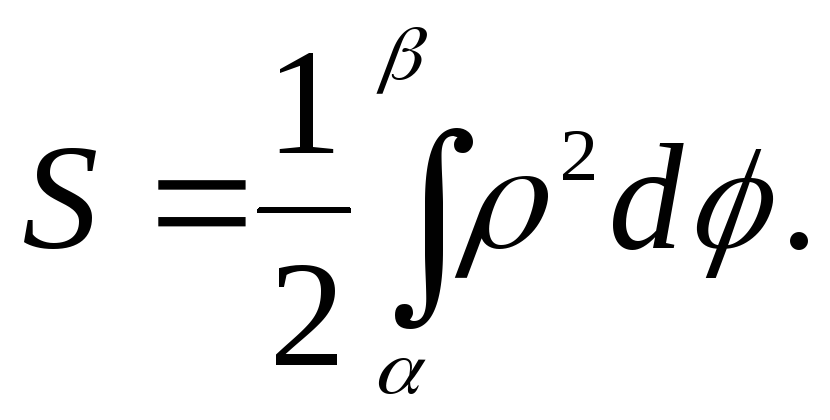
4. 4. 3. Об’єм тіла обертання

Нехай , монотонно-неспадна. Розглянемо фігуру, обмежену прямими та графік . Нехай дана фігура обертається навколо осі ОХ. Знайдемо об’єм тіла, яке утвориться в результаті обертання. При цьому ми будемо використовувати таку інформацію:

Об’єм прямого циліндричного тіла, в основі якого лежить яка-небудь фігура дорівнює площі цієї фігури на помножену на висоту циліндра.

Приступимо тепер до виведення формули об’єму нашого тіла. Візьмемо розбиття відрізка

Через точки розбиття, перпендикулярно до осі проведемо площини, які розбивають тіло на елементарних тіл. Потім займемося обчисленням об’єму елементарного тіла, яке лежить між площинами Візьмемо довільну точку і через цю точку знову проведемо січну площину перпендикулярно до осі . Вона перетне наше елементарне тіло по якійсь фігурі , площа якої дорівнює . Замінимо далі наше елементарне тіло циліндричним тілом, в основі якого лежить фігура і висота якого . Тоді об’єм цього циліндричного тіла, як ми відмічали вище:

Цю величину можна прийняти за табличне значення нашого елементарного тіла. Тоді сума буде наближеним значенням об’єму нашого тіла, причому, оскільки неперервна, то точність цього наближення буде тим вищою, чим менший крок розбиття. Тоді логічно за об’єм цього тіла прийняти границю останньої суми коли (якщо ця границя існує). Оскільки сума під знаком границі є інтегральною для , яка неперервна на , то міркуючи як і в попередніх випадках легко переконатися, що:

1. Це тіло має об’єм;

2. Об’єм шукається за формулою:

З тільки що одержаної формули легко одержати ще одне дуже важливе твердження.

Нехай функція невід’ємна і неперервна на відрізку . Знову розглянемо криволінійну трапецію, обмежену прямими і графіком функції . Будемо вважати, що ця трапеція є плоскою матеріальною пластинкою. При обертанні цієї пластинки навколо осі ми одержимо деяке тіло (тіло обертання). Знайдемо його об’єм.

Площина, перпендикулярна до осі , що проходить через вісь перетинає це тіло по кругу радіуса . Отже площа перетину . Значить, за доведеною вище формулою:

Використовуючи одержані вище формули можна розв’язати багато задач з елементарної геометрії, наприклад, знайти об’єм піраміди, конуса (зрізаних також), кулі, її частин.