
- •Паскевич Тетяна Іванівна магістерська робота електронний посібник для поглибленого вивчення математики учнями математичних ліцеїв та шкіл
- •1. 1. Поняття про електронний підручник
- •1. 2. Основні вимоги до електронного підручника
- •1. 3. Структуризація та оформлення електронного підручника
- •1. 3. 1. Особливості мови html
- •1. 3. 2. Редагування тексту
- •3Адання заголовків
- •1. 3. 3. Створення гіперпосилань і графіки на Web-cторінках
- •1. 3. 4. Робота з таблицями
- •1. 4. Програма Advanced Grapher.
- •1. 5. Етапи створення посібника
- •2. 1. Границя послідовності
- •2. 1. 1. Деякі позначення і термінологія
- •2. 1. 2. Числові послідовності та їх класифікація
- •2. 1. 3. Нескінченно малі послідовності та їх властивості
- •2. 1. 4. Границя послідовності
- •2. 1. 5. Граничний перехід в нерівностях
- •2. 1. 6. Нескінченно великі послідовності
- •2. 2. Теорія дійсних чисел
- •2. 2. 1. Теорія дійсних чисел
- •Порівняння дійсних чисел
- •Властивість транзитивності
- •Додавання дійсних чисел
- •Віднімання дійсних чисел.
- •Множення дійсних чисел
- •Частка двох дійсних чисел
- •Інші властивості дійсних чисел
- •2. 2. 2. Точні грані множини
- •2. 2. 3. Поняття підпослідовності. Теорема Больцано-Вейєрштрасса. Поняття часткової границі. Верхні і нижні границі, проблема їх існування
- •2. 2. 4. Критерій Коші збіжності послідовності
- •2. 3. Границя і неперервність функції
- •2. 3. 1. Гранична точка множини. Означення границі функції
- •2. 3. 2. Границя функції на нескінченності (випадок, коли )
- •2. 3. 3. Односторонні границі функції в точці
- •Перша цікава границя.
- •2. 3. 4. Означення неперервності функції в точці. Точки розриву функції та їх класифікація
- •2. 3. 5. Арифметичні операції над неперервними функціями
- •Одностороння неперервність функції в точці
- •2. 3. 6. Властивості неперервних функцій
- •Локальна властивість
- •2. Глобальні властивості
- •2. 3. 7. Обернена функція
- •2. 4. Показникова та логарифмічна функції і їх властивості
- •2. 4. 1. Степінь з раціональним показником. Показникова функція та її властивості
- •2. 4. 2. Логарифмічна функція
- •2. 4. 3. Загальностепенева функція і її властивості
- •2. 4. 4. Друга та інші цікаві границі
- •2. 4. 5. Гіперболічні функції та їх графіки
- •3. 1. Похідна та її обчислення
- •3. 1. 1. Поняття дотичної до кривої. Кутовий коефіцієнт дотичної
- •3. 1. 2. Диференційованість функції в точці. Зв’язок її з неперервністю і існуванням похідної
- •3. 1. 3. Правила диференціювання
- •3. 1. 4. Диференціал функції та його застосування
- •3. 1. 5. Похідні і диференціали вищих порядків
- •3. 1. 6. Параметрично задані функції і обчислення їх похідних
- •3. 1. 7. Теореми про середнє. І, іі правила Лопіталя. Критерій строгої монотонності функції
- •3. 2. Дослідження функції та побудова її графіку
- •3. 2. 1. Дослідження функції на екстремум
- •3. 2. 2. Дослідження функції диференційованої на відрізку на найбільше та найменше її значення на цьому ж відрізку
- •3. 2. 3. Опуклість і вгнутість графіка функції. Теорема про достатні умови опуклості, вгнутості функції на проміжку
- •3. 2. 4. Точки перегину графіка функції та їх відшукання
- •3. 2. 5. Асимптоти графіка функції
- •4. 1. Невизначений інтеграл
- •4. 1. 1. Первісна. Невизначений інтеграл
- •4. 1. 2. Заміна змінних у невизначеному інтегралі. Інтегрування за частинами
- •4. 2. Інтегрування різних класів функцій
- •4. 2. 1. Інтегрування раціональних функцій
- •4. 2. 2. Інтегрування деяких класів ірраціональних функцій
- •4. 2. 3. Інтегрування ірраціональних функцій з квадратним тричленом під квадратним коренем. Підстановки Ейлера
- •4. 2. 4. Підстановки Чебишева
- •4. 2. 5. Інтегрування тригонометричних функцій
- •4. 3. Інтеграл Рімана
- •4. 3. 1. Суми Дарбу. Їх властивості та означення інтеграла Рімана
- •4. 3. 2. Рівномірно-неперервні функції. Теорема Кантора
- •4. 3. 3. Друге означення інтеграла Рімана
- •4. 3. 4. Властивості інтеграла Рімана
- •4. 3. 5. Інтеграл із змінною верхньою межею. Його властивості
- •4. 3. 6. Формула Ньютона-Лейбніца (основна формула інтегрального числення). Інтегрування методом підстановки та за частинами
- •4. 4. Застосування інтеграла Рімана
- •4. 4. 1. Площа криволінійної трапеції
- •4. 4. 2. Площа криволінійного сектора.
- •4. 4. 3. Об’єм тіла обертання
- •4. 4. 4. Довжина дуги кривої
- •4. 4. 5. Площа поверхні обертання
- •4. 4. 6. Координати центра ваги матеріальної дуги та пластинки. Теореми Гульдена
4. 3. 6. Формула Ньютона-Лейбніца (основна формула інтегрального числення). Інтегрування методом підстановки та за частинами
Теорема 1 (Формула Ньютона-Лейбніца).
Нехай
![]() первісна до
первісна до
![]() на відрізку
на відрізку
![]() .
Якщо
.
Якщо
![]() ,
то має місце рівність:
,
то має місце рівність:
![]()
Доведення.
Візьмемо
![]() –розбиття
відрізка
–розбиття
відрізка
![]() ,
розглянемо суму:
,
розглянемо суму:
![]()
(Оскільки
![]() диференційована на всьому відрізку
диференційована на всьому відрізку
![]() ,
то вона диференційована і тим більше
на кожному з елементарних відрізків,
тоді до неї на кожному з відрізків
розбиття можна застосувати Теорему
Лагранжа, згідно з якою
,
то вона диференційована і тим більше
на кожному з елементарних відрізків,
тоді до неї на кожному з відрізків
розбиття можна застосувати Теорему
Лагранжа, згідно з якою
![]() .)
.)
![]() .
.
Тобто,
ми отримали, що
![]() ,
де
,
де
![]() – довільне розбиття відрізка
– довільне розбиття відрізка
![]() ,
,
![]() – спеціальний вибір точок
– спеціальний вибір точок
![]() (теорема Лагранжа здійснює це вибір).
Оскільки функція
(теорема Лагранжа здійснює це вибір).
Оскільки функція
![]() ,
то перейшовши в останній рівності до
границі, коли
,
то перейшовши в останній рівності до
границі, коли
![]() ,
ми отримаємо:
,
ми отримаємо:
![]() .
.
(Спеціальний
вибір
![]() тут зовсім не шкодить, бо інтегрованість
дана за умовою).
тут зовсім не шкодить, бо інтегрованість
дана за умовою).
Теорема доведена.
З теореми одержується:
Наслідок 1.
Якщо
![]() ,
то
,
то
![]() ,
де
,
де
![]() її первісна на
її первісна на
![]() .
.
Досвід пошуку невизначеного інтеграла підказує нам, що там часто ефективними були теореми про заміну змінних і інтегрування за частинами. Цікаво чи «перекинуться» ці теореми на інтеграл Рімана. –Так.
Теорема 2 (заміна змінних в інтегралі Рімана).
Нехай
![]() ,
а
,
а
![]() – неперервна разом зі своєю похідною
на відрізку
– неперервна разом зі своєю похідною
на відрізку
![]() ,
причому
,
причому
![]() ,
,
![]() і при змінні
і при змінні
![]() від
від
![]() до
до
![]()
![]() змінюється
від
змінюється
від
![]() до
до
![]() .
Тоді справедливі рівності:
.
Тоді справедливі рівності:
![]() (1)
(1)
Доведення.
Візьмемо
довільне
![]() розбиття
відрізка
розбиття
відрізка
![]() .
.
![]()
![]()
Таким
чином ми одержали якесь
![]() розбиття
відрізка
розбиття
відрізка
![]() .
.
![]()
Розглянемо далі різницю:
![]()
(До
останнього ми прийшли, використавши
теорему Лагранжа для функції
![]() ).
Позначимо через
).
Позначимо через
![]() ,
,
![]() .
Утворимо далі наступну інтегральну
суму
.
Утворимо далі наступну інтегральну
суму
![]() ,
де
,
де
![]() – це вибір точок
– це вибір точок
![]() .
.
![]() .
.
(де
![]() –
означає якийсь спеціальний, за рахунок
теореми Лагранжа, вибір точок на відрізку
–
означає якийсь спеціальний, за рахунок
теореми Лагранжа, вибір точок на відрізку
![]() зміни
зміни
![]() ).
Отже, ми довели таку рівність:
).
Отже, ми довели таку рівність:
![]() (2)
(2)
Оскільки
функція
![]() неперервна на відрізку
неперервна на відрізку
![]() ,
то при
,
то при
![]()
![]()
![]() .
Тоді, перейшовши в (2) до границі, при
.
Тоді, перейшовши в (2) до границі, при
![]() і врахувавши тільки що сказане, а також
інтегрованість функції
і врахувавши тільки що сказане, а також
інтегрованість функції
![]() на
на
![]() і
і
![]() на
на
![]() одержимо потрібну нам рівність (1).
одержимо потрібну нам рівність (1).
Теорема доведена.
Теорема 3 (Інтегрування за частинами).
Нехай
![]() і
і
![]() – неперервні зі своїми похідними на
– неперервні зі своїми похідними на
![]() функції. Тоді
функції. Тоді
![]()
Доведення.
Ця
рівність легко одержується з рівності
![]() і доведеної вище формули Ньютона-Лейбніца.
і доведеної вище формули Ньютона-Лейбніца.
![]() .
.
![]()
Враховуючи,
що
![]() є первісною
є первісною
![]() ,
то можна переписати
,
то можна переписати

![]()
Теорема доведена.
4. 4. Застосування інтеграла Рімана
4. 4. 1. Площа криволінійної трапеції
Нехай
![]() ,
монотонно-неспадна. Розглянемо фігуру,
обмежену прямими
,
монотонно-неспадна. Розглянемо фігуру,
обмежену прямими
![]() та графік
та графік
![]() .
Її називають криволінійною
трапецією
. Поставимо завдання обчислити площу
цієї трапеції.
.
Її називають криволінійною
трапецією
. Поставимо завдання обчислити площу
цієї трапеції.
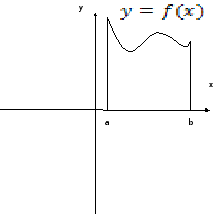
Для
розв’язання цієї задачі візьмемо
будь-яке
![]() розбиття
відрізка
розбиття
відрізка
![]() і утворимо нижню та верхню суми Дарбу
нашої функції по
і утворимо нижню та верхню суми Дарбу
нашої функції по
![]() розбитті.
Як ми знаємо, геометрично ці суми являють
собою площі многокутників, які відповідно
містять цю криволінійну трапецію.
Оскільки функція
розбитті.
Як ми знаємо, геометрично ці суми являють
собою площі многокутників, які відповідно
містять цю криволінійну трапецію.
Оскільки функція
![]() ,
то вона інтегрована за Ріманом, а значить
приведені вище суми Дарбу при
,
то вона інтегрована за Ріманом, а значить
приведені вище суми Дарбу при
![]() прямуватимуть до однієї і тієї ж границі,
яка, як ми знаємо з відповідних Лем і
інтегрованості функції – буде інтегралом
Рімана
прямуватимуть до однієї і тієї ж границі,
яка, як ми знаємо з відповідних Лем і
інтегрованості функції – буде інтегралом
Рімана
![]()
Оскільки криволінійна трапеція весь час знаходиться між вказаними вище многокутниками, логічно за площу цієї трапеції прийняти цю границю. (Цим ми означили, що розуміти під площею криволінійної трапеції). Отже, ми встановили, що таке площа криволінійної трапеції і чому вона дорівнює:
![]()
Нехай
тепер ми маємо криволінійну трапецію,
яка обмежена прямими
![]() і функціями
і функціями
![]() ,
які неперервні і для
,
які неперервні і для
![]() .
.
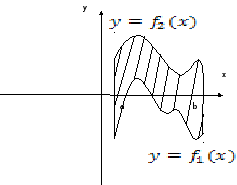
Для
обчислення площі цієї трапеції поступимо
наступним чином. Зробимо паралельне
перенесення площі криволінійної трапеції
на деякий вектор, паралельний до осі
![]() так, щоб найнижча точка графіка функції
так, щоб найнижча точка графіка функції
![]() були або на осі
були або на осі
![]() ,
або вище цієї осі. Тоді площа криволінійної
трапеції дорівнюватиме площі вихідної
трапеції, причому нова буде обмежена з
боків тими самими прямими.
,
або вище цієї осі. Тоді площа криволінійної
трапеції дорівнюватиме площі вихідної
трапеції, причому нова буде обмежена з
боків тими самими прямими.
Маємо
![]() і
і
![]() ,
де
,
де
![]() – якесь стале число, причому для
– якесь стале число, причому для
![]() .
.
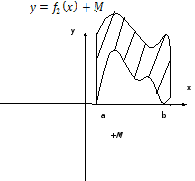
Площа
криволінійної трапеції буде дорівнювати
різниці площ двох трапецій, обидві з
яких обмежені прямими
![]()
![]() і знизу –
і знизу –
![]() і графіками функцій
і графіками функцій
![]() і
і
![]() .
Тоді будемо мати за попередньою формулою
що
.
Тоді будемо мати за попередньою формулою
що
![]()
Отже,
ми одержали, що площа вихідної трапеції,
яка обмежена з боків прямими
![]()
![]() і знизу –
і знизу –
![]() і графіками функцій
і графіками функцій
![]() і
і
![]() обчислюється так
обчислюється так
![]()
Зауважимо, що якщо фігура на площині не підпадає ні під першу ні під другу трапеції, то її розбивають на частинки, кожна з яких буде або типу першої, або типу другої.
