4. 3. 4. Властивості інтеграла Рімана

Властивість 1.

Якщо , то

Доведення.

Для доведення скористаємося означенням і складемо інтегральну суму , виконавши довільне розбиття, де– крок розбиття.

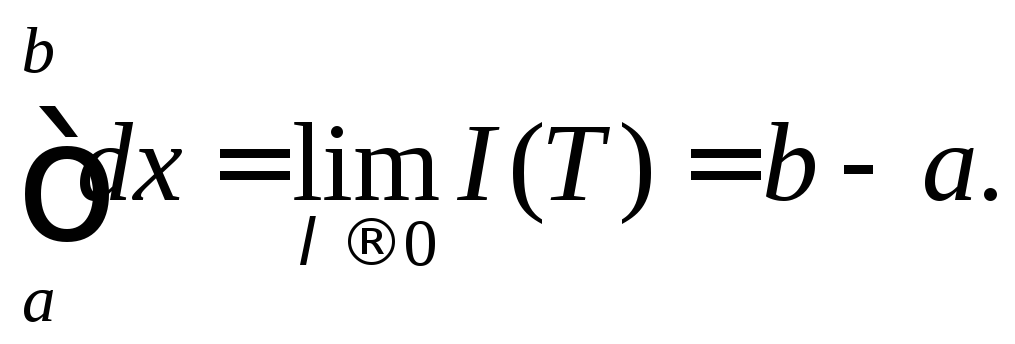
Властивість 2.

Якщо інтегрована на, то вона буде інтегрованою і на відрізку.

.

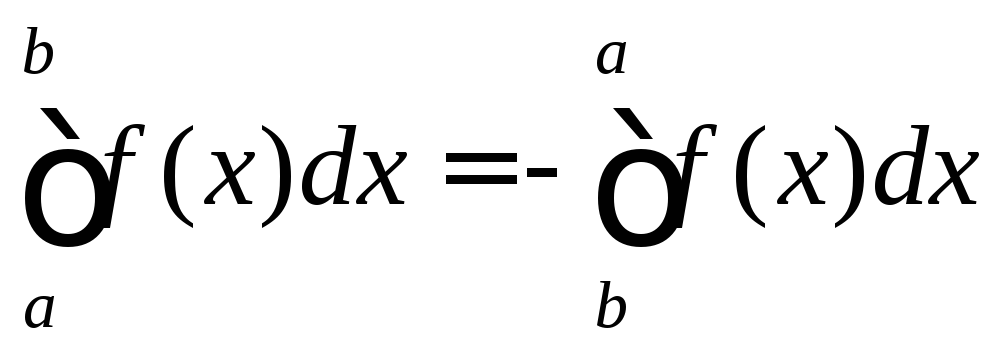Доведення.

Розглянемо довільне –розбиття

;

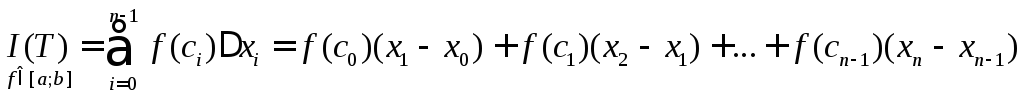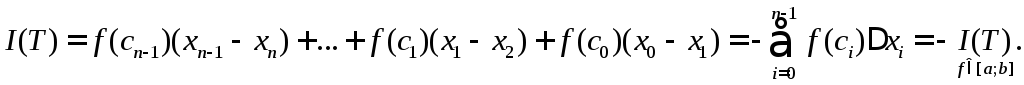Перейшовши в останній рівності до границі маємо

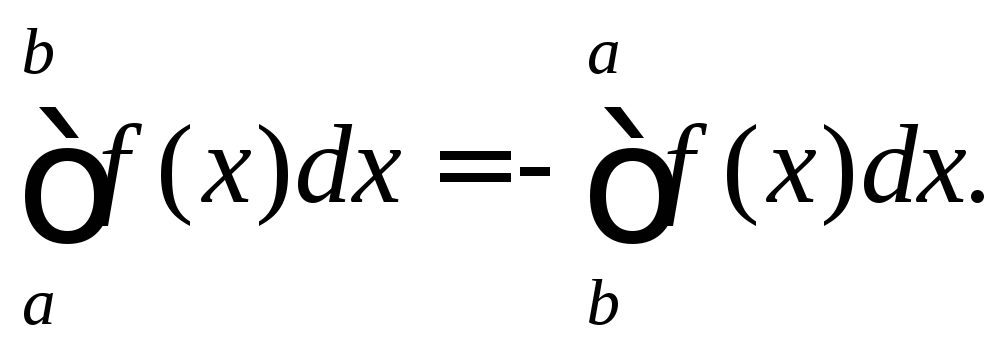
З даної властивості випливає часто вживаний наслідок

Наслідок 1.

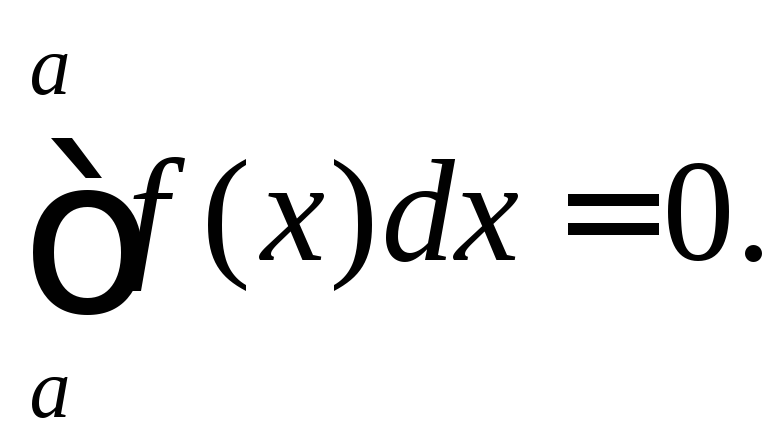
Доведення.

Покладемо

;

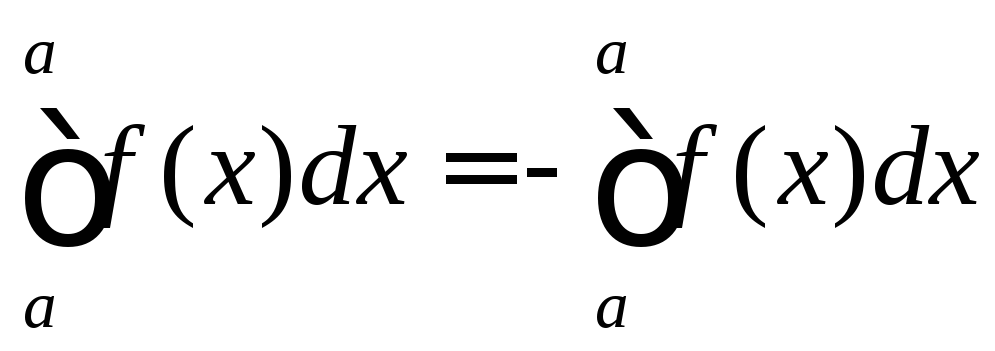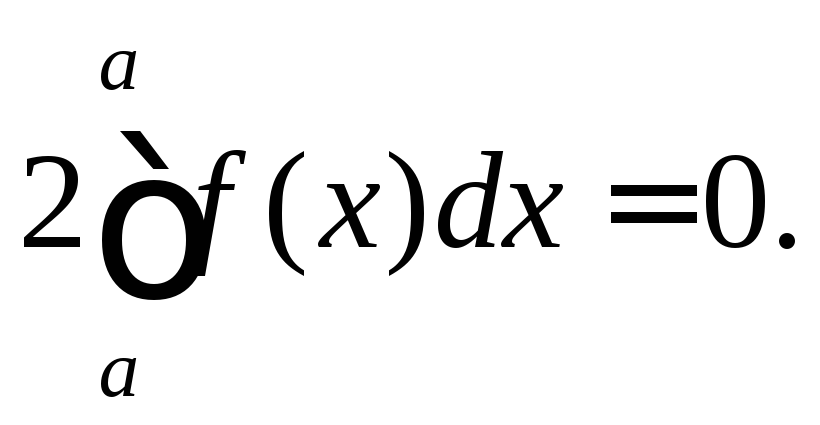
Властивість 3.

Нехай інтегрована на. Тоді вона буде інтегрованою на

Доведення.

Для доведення скористаємося властивостями сум Дарбу і виконаємо розбиття відрізкаірозбиття відрізка. На основі властивостей сум Дарбу одержимо, що

;

Перейдемо до границі і, на основі Критерію інтегрованості функції за Ріманом, одержимо, що

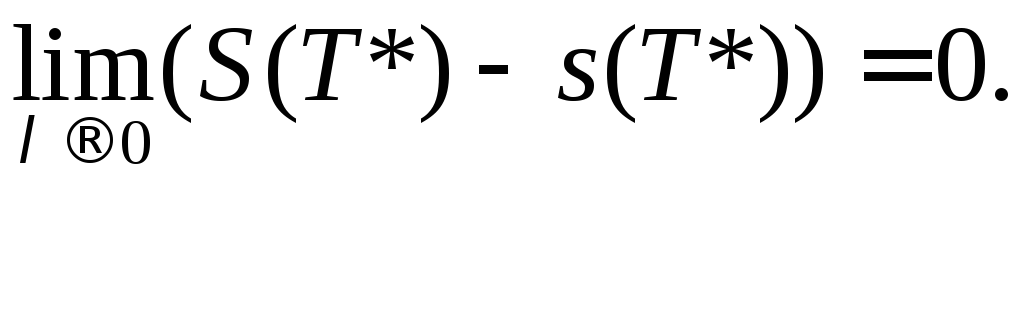
А це і означає інтегрованість на.

Властивість 4.

Нехай інтегрована на, тоді вона такою ж буде на кожному з відрізківіПричому

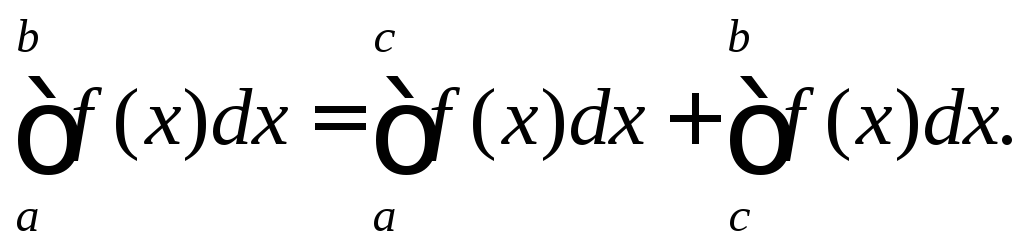
Доведення.

Розглянемо довільне розбиття відрізкаі складемо інтегральну суму

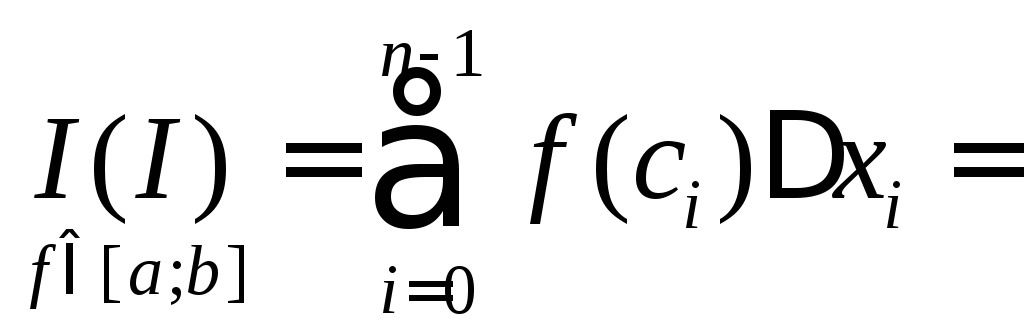
(Якщо , то дана сума розіб’ється на дві)

В будуть лише точки віддо, а в– віддо. Перейшовши до границі, одержимо шукану рівність.

Зауваження 1.Дану властивість можна поширити на будь-яке скінчене число точок поділу відрізка.

Властивість 5.

Якщо інтегрована на, то також інтегрованою тут буде функція

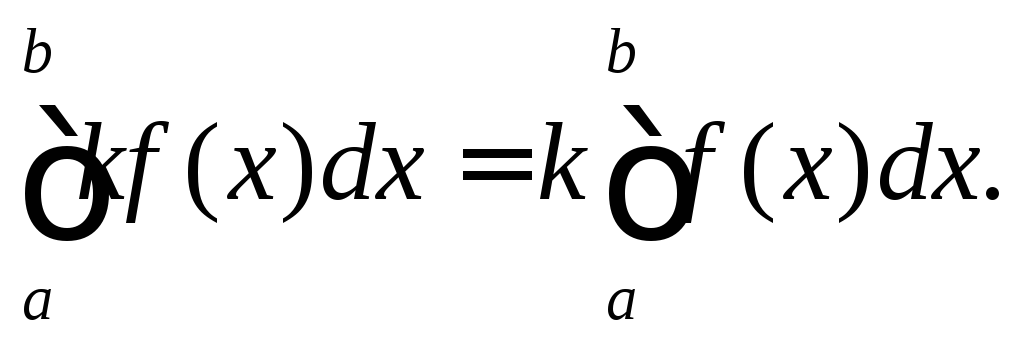
Доведення.

Побудуємо суму

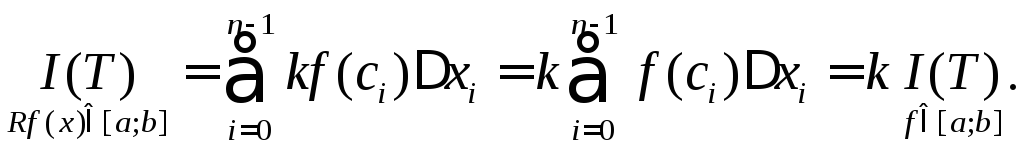
Перейшовши до границі, одержуємо потрібну рівність.

Властивість 6.

Якщо функції іє інтегрованими на, то такими ж будуть

на ,

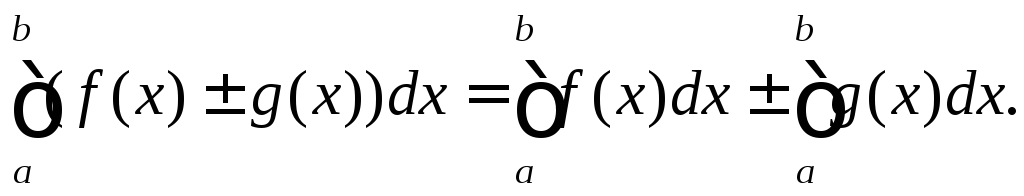
Дана властивість називається Властивістю адитивності.

Доведення.

Виконаємо розбиття відрізкаі, скориставшись умовою матимемо, що

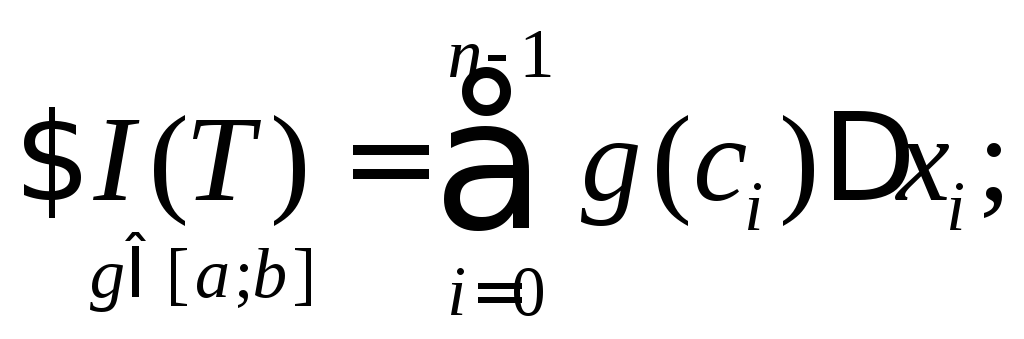
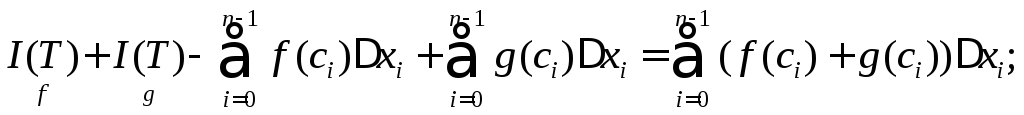
Перейшовши до границі, отримаємо шукану рівність.

Зауваження 2.

В загальному ця властивість може бути поширена на будь-яке скінчене число функцій.

Властивість 7.

Якщо то такий самий знак має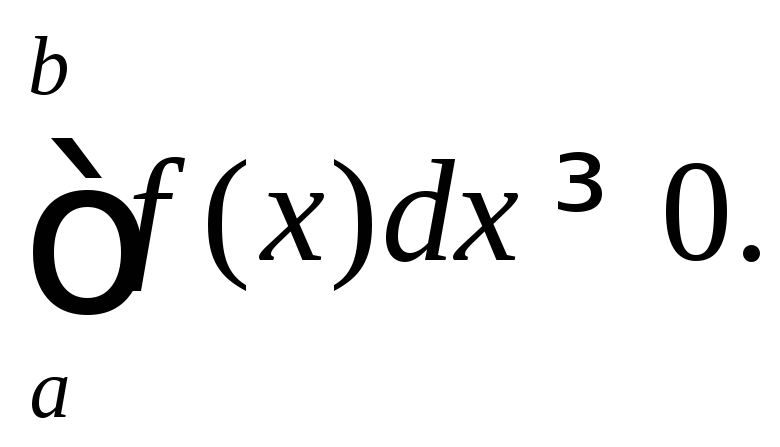

Доведення.

Побудуємо інтегральну суму.

Перейшовши до границі, отримаємо шукане.

Властивість 8.

Якщо функції іє інтегрованими наіто

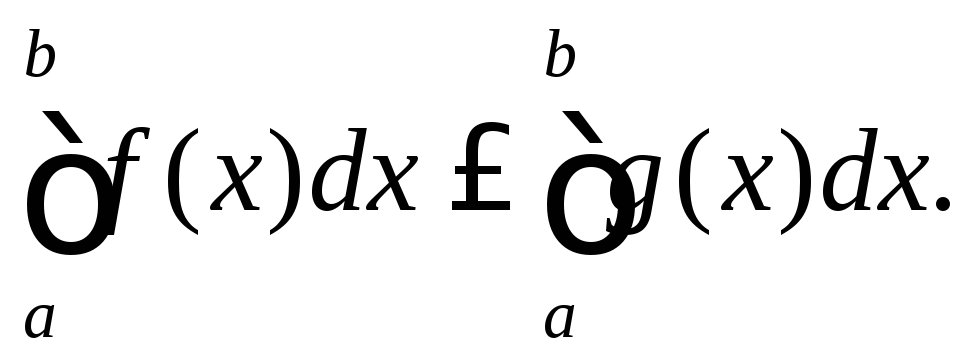
Доведення.

Розглянемо допоміжну функцію Тоді, використовуючи властивості 6 і 7 одержимо доведення даної. Пропонуємо довести самостійно.

Властивість 9.

Якщо інтегрована на, то такою ж тут є, причому має місце така нерівність

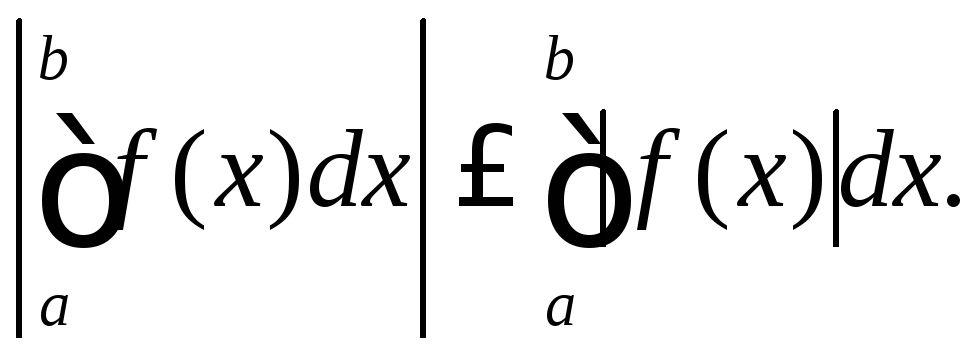
Доведення пропонуємо провести самостійно.

Властивість 10 (Теорема про середнє).

Якщо неперервна нато існує точкатака, що

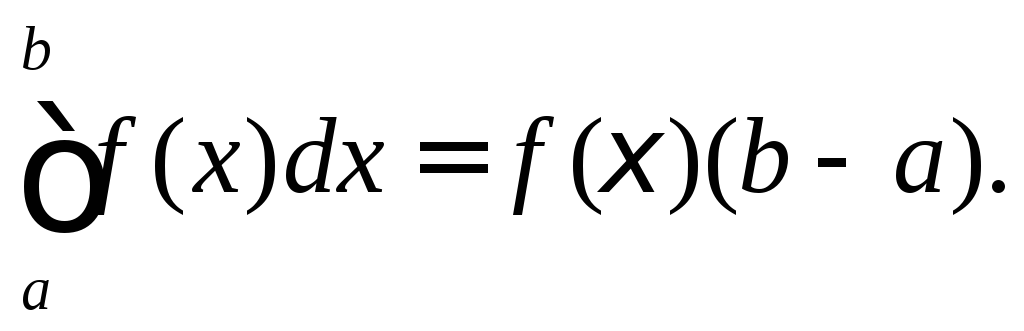
Доведення.

Оскільки є неперервною, то, по-перше, вона інтегрована наа по-друге , за ІІ теоремою Веєрштраса

Враховуючи, щоє інтегрованою, то одержимо, що

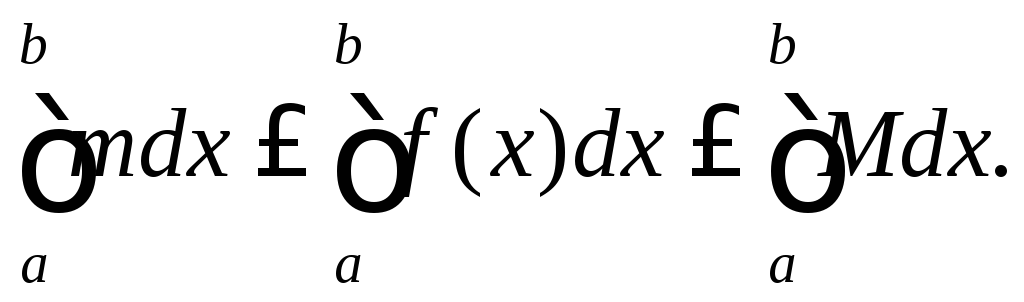
З останньої властивості, за Властивістю 5 маємо

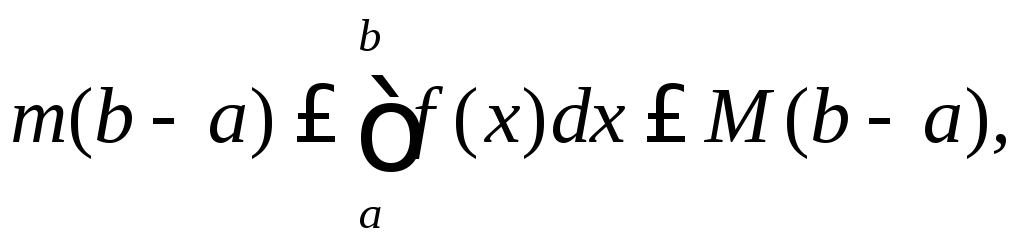
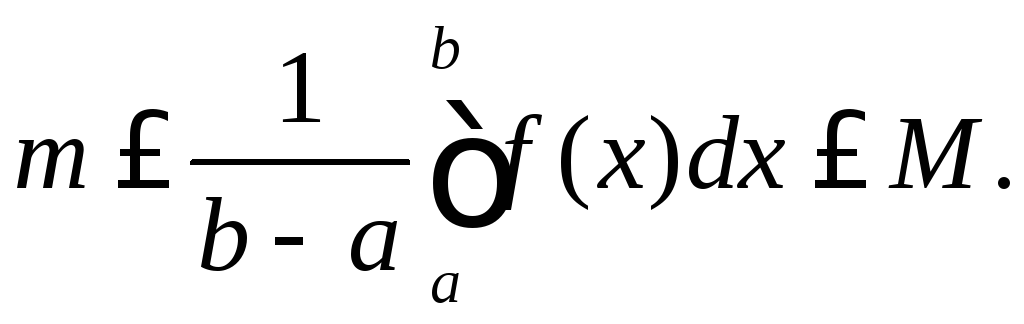
В останній нерівності розглянемо число 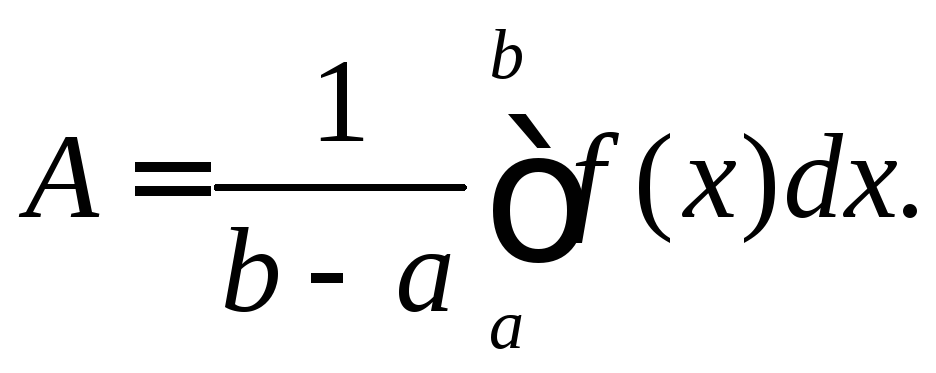Очевидно, що, то за ІІ теоремою Больцано-Коші існує точкатака, що Тоді

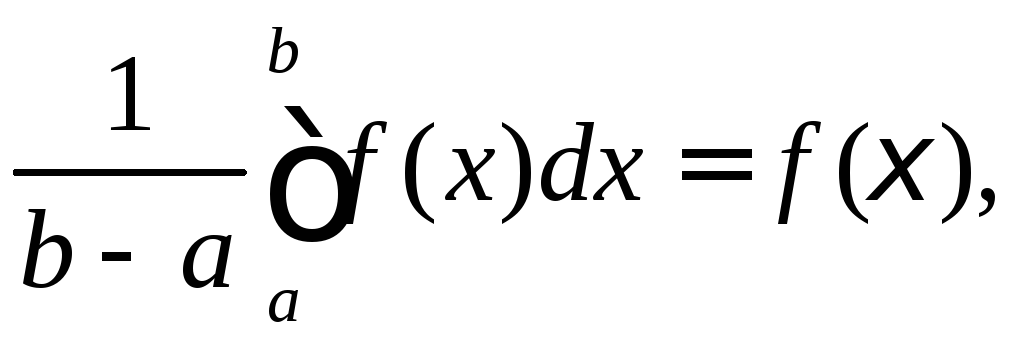
звідки

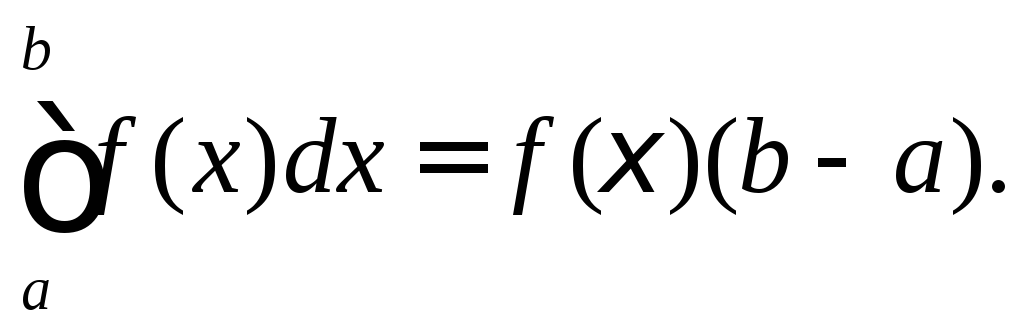
Теорема доведена.

4. 3. 5. Інтеграл із змінною верхньою межею. Його властивості

Нехай , тоді, як ми знаємо, .

А значить, ми маємо функцію:

Спробуємо вивчити властивості цієї функції.

Теорема 1 .

Якщо , то .

Доведення.

Візьмемо . Розглянемо

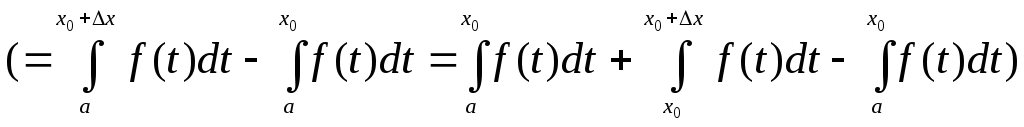
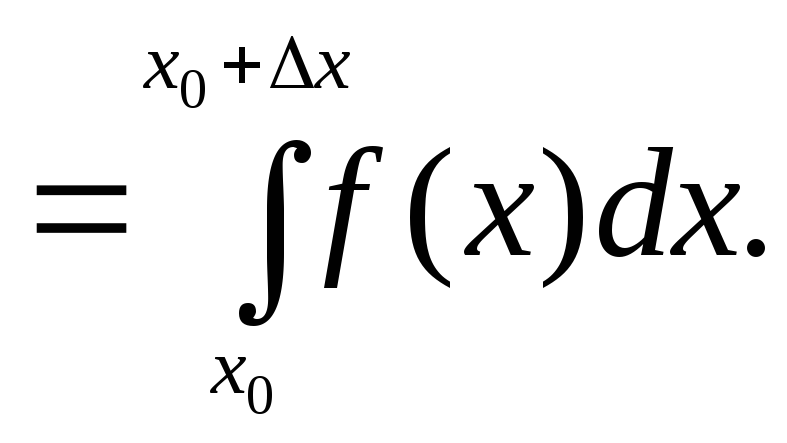
З цієї рівності

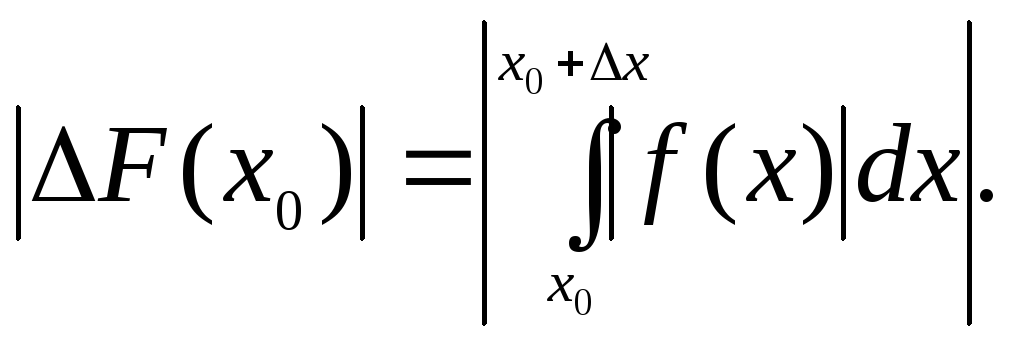
Оскільки , то обмежена на .

;

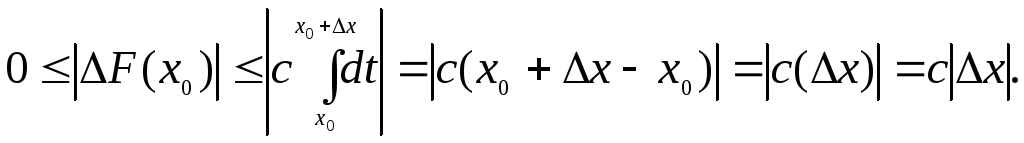
З цієї нерівності маємо

А це, за різницевим означенням, і означає, що ми довели теорему.

Оскільки неперервність більш жорстка вимога на функцію ніж інші, то попередня теорема наводить нас на думку, що інтегрування покращує властивості функції. Наступна теорема нас ще більше переконає в правильності цього висловлювання.

Теорема 2.

Якщо і неперервна в точці , то диференційована в точці і справедлива рівність .

Доведення.

Розглянемо таку різницю:

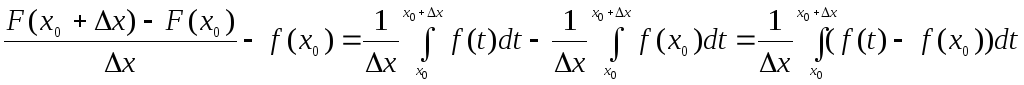
(2)

Оскільки неперервна в точці , то за означенням маємо:

то (3)

Візьмемо далі . Тоді величина , а отже , де – змінна інтегрування в правій частині рівності (2). Тоді з останньої рівності (3) і (2) зразу одержимо наступне:

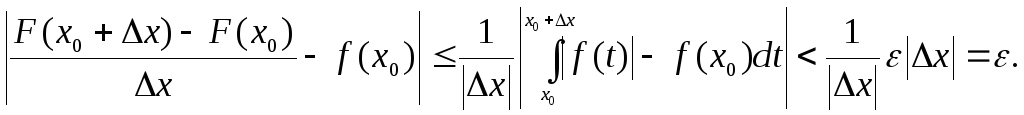
А це означає, що

,

а остання нерівність і показує, що

1) диференційована в точці , (бо існує похідна від неї).

2) справедлива рівність .

Теорема доведена.

З Теореми 2, як наслідок, одержуємо важливе твердження, яке було нам потрібне в розділі «Невизначений інтеграл», але ми там його отримати не могли.

Наслідок 1.

Якщо , то функція диференційована на і

Тобто: Кожна неперервна на відрізку функція має первісну на цьому відрізку.

Тепер зовсім не складно отримати формулу, яка дозволяє дуже ефективно обчислювати інтеграл Рімана, якщо ми знаємо первісну до підінтегральної функції.