
- •Паскевич Тетяна Іванівна магістерська робота електронний посібник для поглибленого вивчення математики учнями математичних ліцеїв та шкіл
- •1. 1. Поняття про електронний підручник
- •1. 2. Основні вимоги до електронного підручника
- •1. 3. Структуризація та оформлення електронного підручника
- •1. 3. 1. Особливості мови html
- •1. 3. 2. Редагування тексту
- •3Адання заголовків
- •1. 3. 3. Створення гіперпосилань і графіки на Web-cторінках
- •1. 3. 4. Робота з таблицями
- •1. 4. Програма Advanced Grapher.
- •1. 5. Етапи створення посібника
- •2. 1. Границя послідовності
- •2. 1. 1. Деякі позначення і термінологія
- •2. 1. 2. Числові послідовності та їх класифікація
- •2. 1. 3. Нескінченно малі послідовності та їх властивості
- •2. 1. 4. Границя послідовності
- •2. 1. 5. Граничний перехід в нерівностях
- •2. 1. 6. Нескінченно великі послідовності
- •2. 2. Теорія дійсних чисел
- •2. 2. 1. Теорія дійсних чисел
- •Порівняння дійсних чисел
- •Властивість транзитивності
- •Додавання дійсних чисел
- •Віднімання дійсних чисел.
- •Множення дійсних чисел
- •Частка двох дійсних чисел
- •Інші властивості дійсних чисел
- •2. 2. 2. Точні грані множини
- •2. 2. 3. Поняття підпослідовності. Теорема Больцано-Вейєрштрасса. Поняття часткової границі. Верхні і нижні границі, проблема їх існування
- •2. 2. 4. Критерій Коші збіжності послідовності
- •2. 3. Границя і неперервність функції
- •2. 3. 1. Гранична точка множини. Означення границі функції
- •2. 3. 2. Границя функції на нескінченності (випадок, коли )
- •2. 3. 3. Односторонні границі функції в точці
- •Перша цікава границя.
- •2. 3. 4. Означення неперервності функції в точці. Точки розриву функції та їх класифікація
- •2. 3. 5. Арифметичні операції над неперервними функціями
- •Одностороння неперервність функції в точці
- •2. 3. 6. Властивості неперервних функцій
- •Локальна властивість
- •2. Глобальні властивості
- •2. 3. 7. Обернена функція
- •2. 4. Показникова та логарифмічна функції і їх властивості
- •2. 4. 1. Степінь з раціональним показником. Показникова функція та її властивості
- •2. 4. 2. Логарифмічна функція
- •2. 4. 3. Загальностепенева функція і її властивості
- •2. 4. 4. Друга та інші цікаві границі
- •2. 4. 5. Гіперболічні функції та їх графіки
- •3. 1. Похідна та її обчислення
- •3. 1. 1. Поняття дотичної до кривої. Кутовий коефіцієнт дотичної
- •3. 1. 2. Диференційованість функції в точці. Зв’язок її з неперервністю і існуванням похідної
- •3. 1. 3. Правила диференціювання
- •3. 1. 4. Диференціал функції та його застосування
- •3. 1. 5. Похідні і диференціали вищих порядків
- •3. 1. 6. Параметрично задані функції і обчислення їх похідних
- •3. 1. 7. Теореми про середнє. І, іі правила Лопіталя. Критерій строгої монотонності функції
- •3. 2. Дослідження функції та побудова її графіку
- •3. 2. 1. Дослідження функції на екстремум
- •3. 2. 2. Дослідження функції диференційованої на відрізку на найбільше та найменше її значення на цьому ж відрізку
- •3. 2. 3. Опуклість і вгнутість графіка функції. Теорема про достатні умови опуклості, вгнутості функції на проміжку
- •3. 2. 4. Точки перегину графіка функції та їх відшукання
- •3. 2. 5. Асимптоти графіка функції
- •4. 1. Невизначений інтеграл
- •4. 1. 1. Первісна. Невизначений інтеграл
- •4. 1. 2. Заміна змінних у невизначеному інтегралі. Інтегрування за частинами
- •4. 2. Інтегрування різних класів функцій
- •4. 2. 1. Інтегрування раціональних функцій
- •4. 2. 2. Інтегрування деяких класів ірраціональних функцій
- •4. 2. 3. Інтегрування ірраціональних функцій з квадратним тричленом під квадратним коренем. Підстановки Ейлера
- •4. 2. 4. Підстановки Чебишева
- •4. 2. 5. Інтегрування тригонометричних функцій
- •4. 3. Інтеграл Рімана
- •4. 3. 1. Суми Дарбу. Їх властивості та означення інтеграла Рімана
- •4. 3. 2. Рівномірно-неперервні функції. Теорема Кантора
- •4. 3. 3. Друге означення інтеграла Рімана
- •4. 3. 4. Властивості інтеграла Рімана
- •4. 3. 5. Інтеграл із змінною верхньою межею. Його властивості
- •4. 3. 6. Формула Ньютона-Лейбніца (основна формула інтегрального числення). Інтегрування методом підстановки та за частинами
- •4. 4. Застосування інтеграла Рімана
- •4. 4. 1. Площа криволінійної трапеції
- •4. 4. 2. Площа криволінійного сектора.
- •4. 4. 3. Об’єм тіла обертання
- •4. 4. 4. Довжина дуги кривої
- •4. 4. 5. Площа поверхні обертання
- •4. 4. 6. Координати центра ваги матеріальної дуги та пластинки. Теореми Гульдена
4. 2. 2. Інтегрування деяких класів ірраціональних функцій
![]() –раціональна
функція. За
–раціональна
функція. За
![]() ми
будемо приймати функцію, що зображується
з допомогою дробу, чисельник і знаменник
якого є многочленами від двох змінних
ми
будемо приймати функцію, що зображується
з допомогою дробу, чисельник і знаменник
якого є многочленами від двох змінних
![]() і
і
![]() .
.
Наприклад.
![]() –є
раціональним;
–є
раціональним;
![]() –не
є раціональним;
–не
є раціональним;
![]()
В цьому параграфі ми покажемо як інтегрувати 3 класи ірраціональних функцій. Найпростішим є випадок:
1)
![]()
Обчислимо інтеграл від такої функції:
![]()
Простий аналіз показує, що в цьому випадку можна спробувати заміну
![]() (1)
(1)
![]()
![]() ;
;
![]()
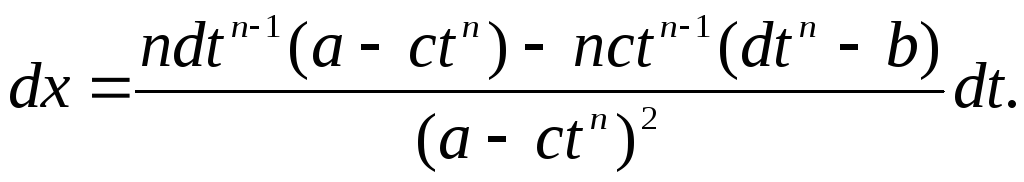
Підставивши
всі одержані вище значення під знак
інтеграла ми побачимо, що підінтегральна
функція є раціональною по
![]() ,
а інтеграл від такої функції ми вміємо
обчислювати. Таким чином підстановка
(1) розв’язує нашу задачу від такої
функції. В цьому випадку кажуть, що
заміна (1) раціоналізує інтеграл.
,
а інтеграл від такої функції ми вміємо
обчислювати. Таким чином підстановка
(1) розв’язує нашу задачу від такої
функції. В цьому випадку кажуть, що
заміна (1) раціоналізує інтеграл.
4. 2. 3. Інтегрування ірраціональних функцій з квадратним тричленом під квадратним коренем. Підстановки Ейлера
Нехай
маємо
![]() .
В цьому випадку також знайдемо підстановки,
які раціоналізують такий інтеграл.
.
В цьому випадку також знайдемо підстановки,
які раціоналізують такий інтеграл.
Для вирішення обчислення такого інтеграла використовують так звані підстановки Ейлера:
Нехай
 ,
тоді
,
тоді
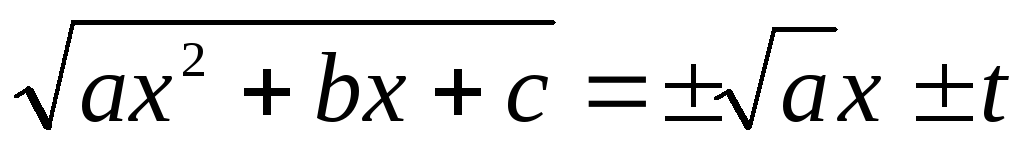 .
.
Знайдемо
![]() (в майбутньому ми будемо брати однакову
комбінацію знаків).
(в майбутньому ми будемо брати однакову
комбінацію знаків).
![]()
![]()
 ,
,
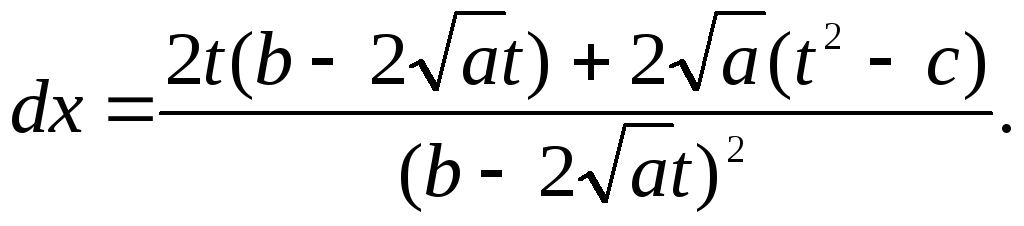
Отже
![]() раціонально виражається через
раціонально виражається через
![]() .
.
Виразимо
корінь через
![]() :
:
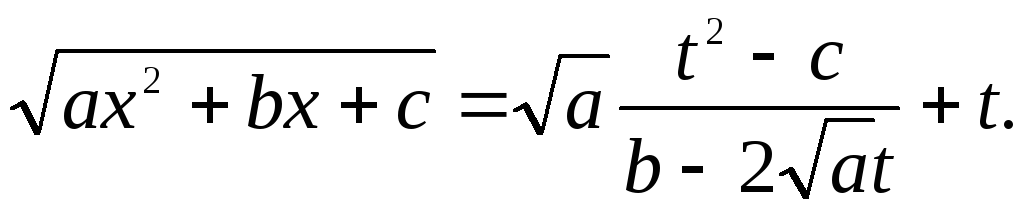
Бачимо,
що і корінь також виражається через
![]() раціонально. Підставивши під знак
інтеграла вирази по
раціонально. Підставивши під знак
інтеграла вирази по
![]() від
від
![]() ,
кореня і
,
кореня і
![]() одержимо під знаком інтеграла раціональну
функцію від
одержимо під знаком інтеграла раціональну
функцію від
![]() .
І отже ми встановили, що в першому випадку
.
І отже ми встановили, що в першому випадку
![]() перша
підстановка Ейлера раціоналізує нам
інтеграл.
перша
підстановка Ейлера раціоналізує нам
інтеграл.
2)
Нехай
![]() ,
тоді
,
тоді
![]()
![]()
![]() ;
;
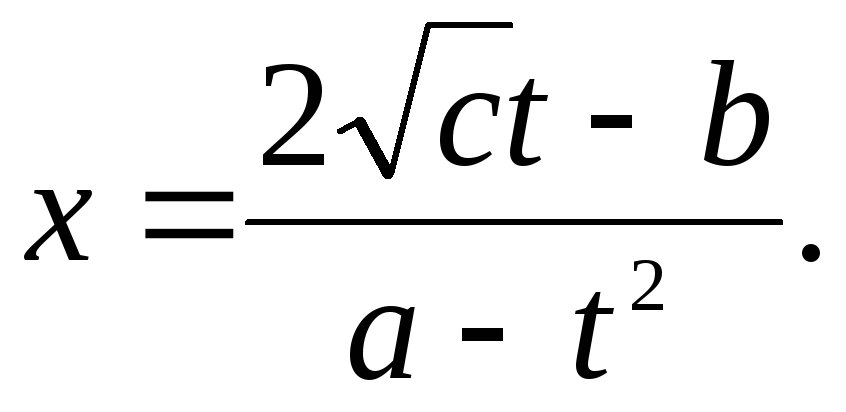
Бачимо,
що
![]() раціонально виражається через
раціонально виражається через
![]() ,
то в деякому випадку корінь теж раціонально
буде виражатися через
,
то в деякому випадку корінь теж раціонально
буде виражатися через
![]() .
Отже функція раціоналізується.
.
Отже функція раціоналізується.
3)
![]() – корені тричлена
– корені тричлена
![]() ,
тоді
,
тоді
![]()
![]()
Значить
![]() раціонально виражається через
раціонально виражається через
![]() .
Значить третя підстановка раціоналізує
наш інтеграл.
.
Значить третя підстановка раціоналізує
наш інтеграл.
Зауважимо, що розглянуті вище 3 підстановки Ейлера повністю вирішують проблему раціоналізації таких інтегралів. Та часто підстановки Ейлера призводять до громіздких виразів, а тому, якщо є можливість обійтися без підстановок Ейлера, то цю можливість слід використовувати.
4. 2. 4. Підстановки Чебишева
Тут ми з’ясуємо як брати інтеграл виду:
![]()
![]() –раціональні
числа,
–раціональні
числа,
![]() – дійсні числа.
– дійсні числа.
Якщо
 – ціле число, то підінтегральна функція
буде із класу найпростіших ірраціональностей,
які ми розглядали вище і в цьому випадку
цей інтеграл раціоналізується ,
– ціле число, то підінтегральна функція
буде із класу найпростіших ірраціональностей,
які ми розглядали вище і в цьому випадку
цей інтеграл раціоналізується ,
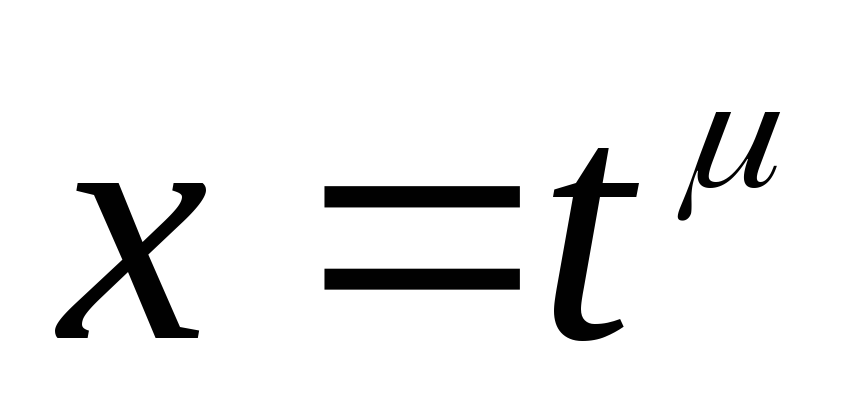 ,
де
,
де
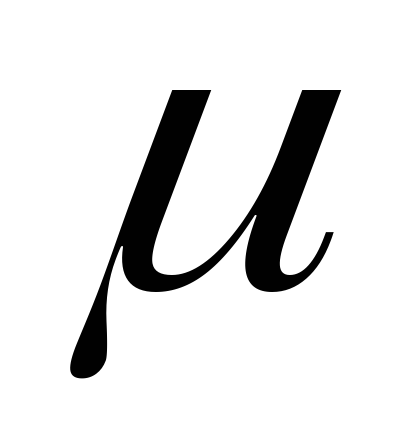 – спільний знаменник чисел
– спільний знаменник чисел
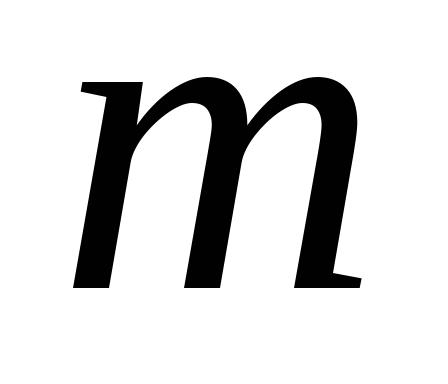 і
і
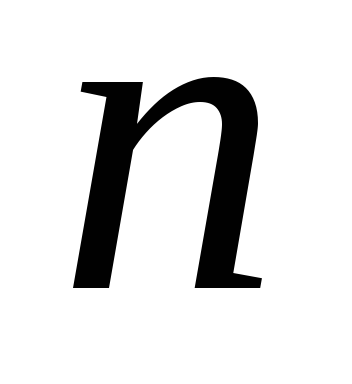 .
.Нехай
 – не ціле, але
– не ціле, але
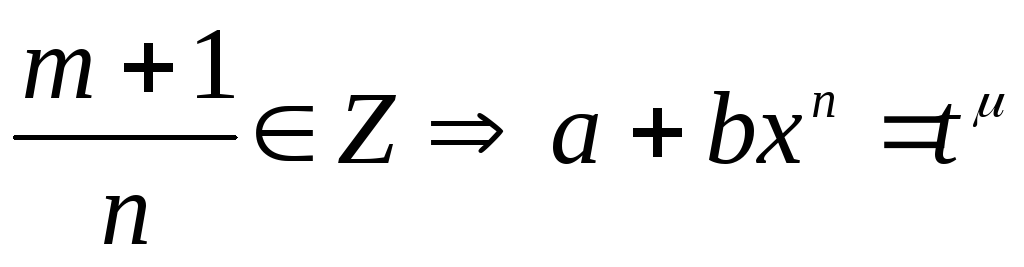 ,
де
,
де
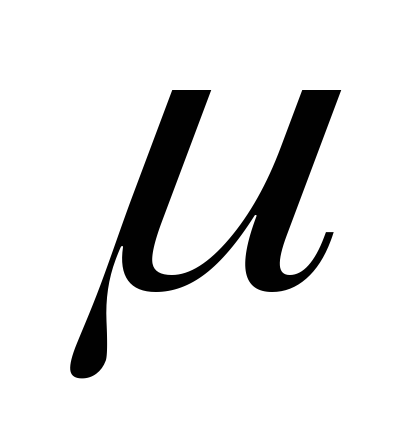 – знаменник числа
– знаменник числа
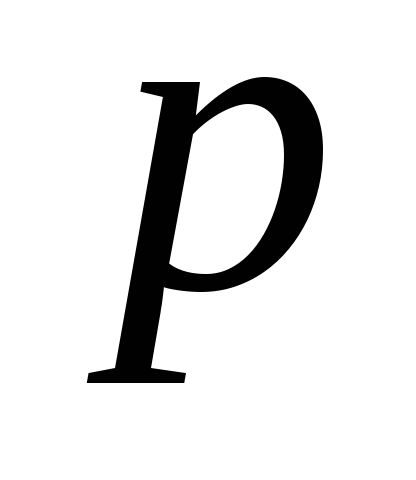 .
.Нехай
 але
але
 .
.
В цьому випадку, щоб вийти на потрібну заміну потрібно дещо перетворити підінтегральний вираз:
![]()
Тоді заміна, яка раціоналізує наш інтеграл матиме вигляд:
![]() ,
де
,
де
![]() – знаменник числа
– знаменник числа
![]() .
.
4)
Якщо
![]()
![]() ,
то цей інтеграл не береться.
,
то цей інтеграл не береться.
4. 2. 5. Інтегрування тригонометричних функцій
Тут ми будемо займатися обчисленням інтегралів виду:
![]() .
.
Ми покажемо далі як можна раціоналізувати такий інтеграл.
Нехай спочатку підінтегральна функція має таку властивість:
 ,
(тобто підінтегральна функція є непарною
відносно
,
(тобто підінтегральна функція є непарною
відносно
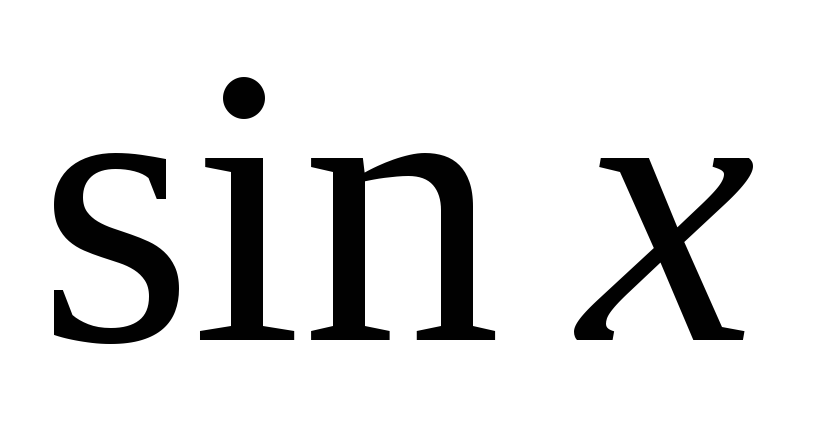 ).
Виявляється, що в цьому випадку інтеграл
раціоналізується з допомогою підстановки
).
Виявляється, що в цьому випадку інтеграл
раціоналізується з допомогою підстановки
 .
Можна довести, що весь підінтегральний
вираз є функцією від косинуса.
.
Можна довести, що весь підінтегральний
вираз є функцією від косинуса.
1.
![]()
![]() ,
,
![]() .
.
2.
![]()
![]() ,
,
![]()
3.
![]()
![]()
В
випадку 3 можна довести, що підінтегральний
вираз буде функцією
![]() Тому такий інтеграл в цьому випадку
раціоналізується за допомогою підстановки:
Тому такий інтеграл в цьому випадку
раціоналізується за допомогою підстановки:
![]() або
або
![]()
Якщо
ж не виконується ні 1 ні 2 ні 3, то тоді,
як ми побачимо нижче, наш інтеграл
раціоналізується з допомогою так званої
Універсальної
тригонометричної підстановки
![]() .
.
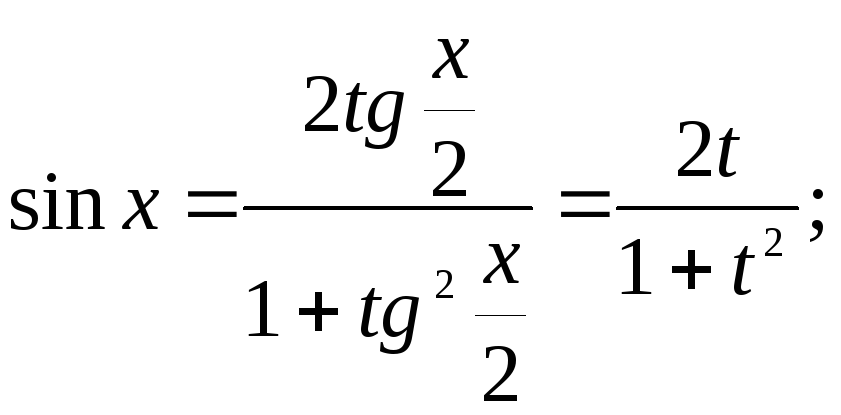
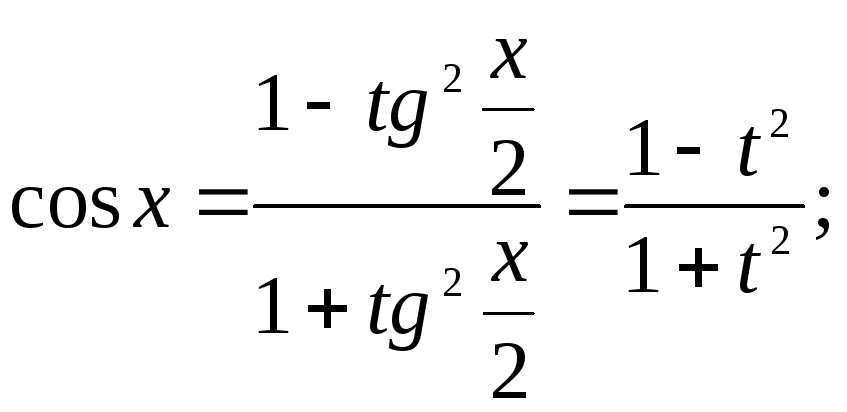
![]()
![]()
Звідси видно, що дійсно універсальна тригонометрична підстановка раціоналізує наш інтеграл.
Зауважимо, що перед тим, як брати заданий інтеграл, треба перевірити чи не виконується одна з умов 1-3 і якщо виконується, то використовувати тільки її, а не універсальну тригонометричну підстановку, тому що остання приводить до складнішої раціональної функції під знаком інтегралу.
Приклад
1.
Обчислити інтеграл:
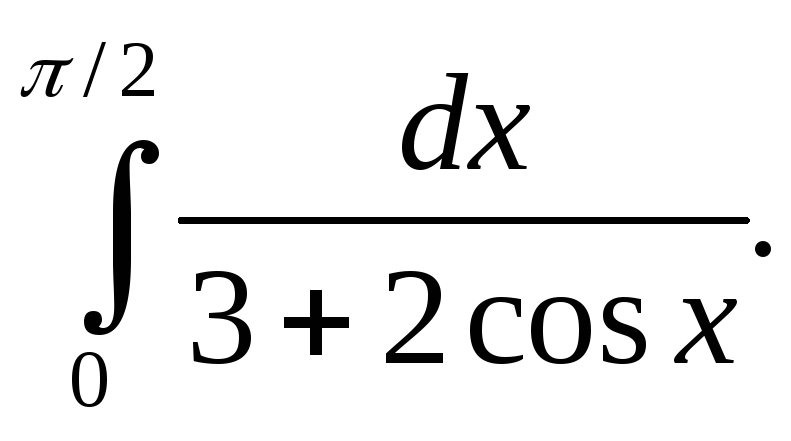
Розв’язання:
Застосуємо універсальну тригонометричну підстановку:
![]()

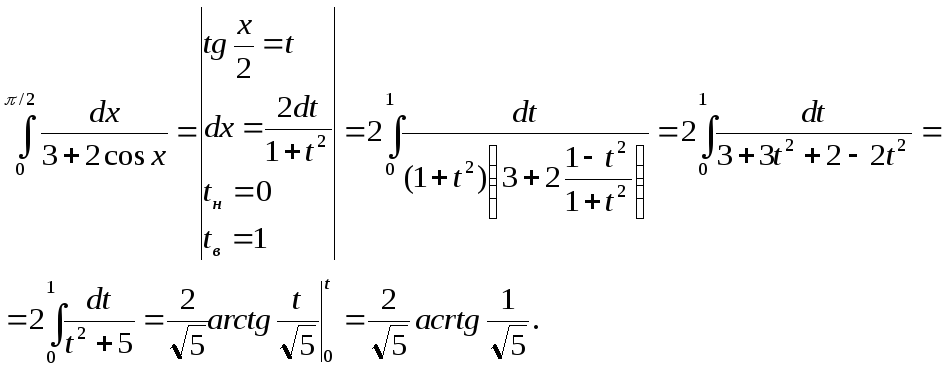
Приклад
2.
Обчислити інтеграл:
![]()
Розв’язання:
Приймаємо
![]() тоді
тоді![]()
Записуємо ці вирази у формулу інтегрування частинами:

