
- •Паскевич Тетяна Іванівна магістерська робота електронний посібник для поглибленого вивчення математики учнями математичних ліцеїв та шкіл
- •1. 1. Поняття про електронний підручник
- •1. 2. Основні вимоги до електронного підручника
- •1. 3. Структуризація та оформлення електронного підручника
- •1. 3. 1. Особливості мови html
- •1. 3. 2. Редагування тексту
- •3Адання заголовків
- •1. 3. 3. Створення гіперпосилань і графіки на Web-cторінках
- •1. 3. 4. Робота з таблицями
- •1. 4. Програма Advanced Grapher.
- •1. 5. Етапи створення посібника
- •2. 1. Границя послідовності
- •2. 1. 1. Деякі позначення і термінологія
- •2. 1. 2. Числові послідовності та їх класифікація
- •2. 1. 3. Нескінченно малі послідовності та їх властивості
- •2. 1. 4. Границя послідовності
- •2. 1. 5. Граничний перехід в нерівностях
- •2. 1. 6. Нескінченно великі послідовності
- •2. 2. Теорія дійсних чисел
- •2. 2. 1. Теорія дійсних чисел
- •Порівняння дійсних чисел
- •Властивість транзитивності
- •Додавання дійсних чисел
- •Віднімання дійсних чисел.
- •Множення дійсних чисел
- •Частка двох дійсних чисел
- •Інші властивості дійсних чисел
- •2. 2. 2. Точні грані множини
- •2. 2. 3. Поняття підпослідовності. Теорема Больцано-Вейєрштрасса. Поняття часткової границі. Верхні і нижні границі, проблема їх існування
- •2. 2. 4. Критерій Коші збіжності послідовності
- •2. 3. Границя і неперервність функції
- •2. 3. 1. Гранична точка множини. Означення границі функції
- •2. 3. 2. Границя функції на нескінченності (випадок, коли )
- •2. 3. 3. Односторонні границі функції в точці
- •Перша цікава границя.
- •2. 3. 4. Означення неперервності функції в точці. Точки розриву функції та їх класифікація
- •2. 3. 5. Арифметичні операції над неперервними функціями
- •Одностороння неперервність функції в точці
- •2. 3. 6. Властивості неперервних функцій
- •Локальна властивість
- •2. Глобальні властивості
- •2. 3. 7. Обернена функція
- •2. 4. Показникова та логарифмічна функції і їх властивості
- •2. 4. 1. Степінь з раціональним показником. Показникова функція та її властивості
- •2. 4. 2. Логарифмічна функція
- •2. 4. 3. Загальностепенева функція і її властивості
- •2. 4. 4. Друга та інші цікаві границі
- •2. 4. 5. Гіперболічні функції та їх графіки
- •3. 1. Похідна та її обчислення
- •3. 1. 1. Поняття дотичної до кривої. Кутовий коефіцієнт дотичної
- •3. 1. 2. Диференційованість функції в точці. Зв’язок її з неперервністю і існуванням похідної
- •3. 1. 3. Правила диференціювання
- •3. 1. 4. Диференціал функції та його застосування
- •3. 1. 5. Похідні і диференціали вищих порядків
- •3. 1. 6. Параметрично задані функції і обчислення їх похідних
- •3. 1. 7. Теореми про середнє. І, іі правила Лопіталя. Критерій строгої монотонності функції
- •3. 2. Дослідження функції та побудова її графіку
- •3. 2. 1. Дослідження функції на екстремум
- •3. 2. 2. Дослідження функції диференційованої на відрізку на найбільше та найменше її значення на цьому ж відрізку
- •3. 2. 3. Опуклість і вгнутість графіка функції. Теорема про достатні умови опуклості, вгнутості функції на проміжку
- •3. 2. 4. Точки перегину графіка функції та їх відшукання
- •3. 2. 5. Асимптоти графіка функції
- •4. 1. Невизначений інтеграл
- •4. 1. 1. Первісна. Невизначений інтеграл
- •4. 1. 2. Заміна змінних у невизначеному інтегралі. Інтегрування за частинами
- •4. 2. Інтегрування різних класів функцій
- •4. 2. 1. Інтегрування раціональних функцій
- •4. 2. 2. Інтегрування деяких класів ірраціональних функцій
- •4. 2. 3. Інтегрування ірраціональних функцій з квадратним тричленом під квадратним коренем. Підстановки Ейлера
- •4. 2. 4. Підстановки Чебишева
- •4. 2. 5. Інтегрування тригонометричних функцій
- •4. 3. Інтеграл Рімана
- •4. 3. 1. Суми Дарбу. Їх властивості та означення інтеграла Рімана
- •4. 3. 2. Рівномірно-неперервні функції. Теорема Кантора
- •4. 3. 3. Друге означення інтеграла Рімана
- •4. 3. 4. Властивості інтеграла Рімана
- •4. 3. 5. Інтеграл із змінною верхньою межею. Його властивості
- •4. 3. 6. Формула Ньютона-Лейбніца (основна формула інтегрального числення). Інтегрування методом підстановки та за частинами
- •4. 4. Застосування інтеграла Рімана
- •4. 4. 1. Площа криволінійної трапеції
- •4. 4. 2. Площа криволінійного сектора.
- •4. 4. 3. Об’єм тіла обертання
- •4. 4. 4. Довжина дуги кривої
- •4. 4. 5. Площа поверхні обертання
- •4. 4. 6. Координати центра ваги матеріальної дуги та пластинки. Теореми Гульдена
3. 2. 4. Точки перегину графіка функції та їх відшукання
Нехай
![]() – функція неперервна в околі точки
– функція неперервна в околі точки
![]() .
Якщо графік функції при переході через
точку
.
Якщо графік функції при переході через
точку
![]() міняє опуклість на вгнутість або навпаки,
то таку точку
міняє опуклість на вгнутість або навпаки,
то таку точку
![]() будемо називати точкою
перегину
графіка функції.
будемо називати точкою
перегину
графіка функції.
Найближчою нашою метою є пошук точок перегину функції. Подібно до екстремуму тут також є
Теорема 1 (Необхідна умова існування точок перегину).
Нехай
![]() неперервна в
неперервна в
![]() і точка
і точка
![]() – точка перегину графіка цієї функції.
Якщо в цій точці існує похідна ІІ порядку,
то вона дорівнює нулю.
– точка перегину графіка цієї функції.
Якщо в цій точці існує похідна ІІ порядку,
то вона дорівнює нулю.
Доведення.
В
загальному об’ємі ми цієї теореми
доводити не будемо, а будемо вимагати
від функції додаткової умови (щоб
спростити доведення), щоб друга похідна
в точці
![]() була неперервною функцією. Отже, нехай
була неперервною функцією. Отже, нехай
![]() – точка перегину функції. І в
– точка перегину функції. І в
![]() існує
існує
![]() ,
яка неперервна в точці
,
яка неперервна в точці
![]() .
Припустимо, що
.
Припустимо, що
![]() .
А значить
.
А значить
![]() або
або
![]() .
Нехай для конкретності
.
Нехай для конкретності
![]() .
Звідси і з неперервності функції
.
Звідси і з неперервності функції
![]() в точці
в точці
![]() ,
за Теоремою про Консервативність
матимемо, що
,
за Теоремою про Консервативність
матимемо, що
![]()
Звідси,
за попередньою теоремою, графік функції
в цьому околі є опуклим. А це неможливо,
бо
![]() – точка перегину і по різні боки від
точки
– точка перегину і по різні боки від
точки
![]() графік матиме різні опуклості.
графік матиме різні опуклості.
Теорема доведена.
З
останнього випливає, що точки перегину
графіка функції слід шукати серед тих,
де
![]() або не існує. Такі точки називатимемо
критичними точками 2.
або не існує. Такі точки називатимемо
критичними точками 2.
Візьмемо
![]() ,
для якої похідна ІІ порядку в точці 0
дорівнює нулю. Але точка 0 не є точкою
перегину цієї функції. Це показує, що
не в кожній критичній точці 2 буде перегин
графіка функції. Отже і тут потрібні
достатні умови.
,
для якої похідна ІІ порядку в точці 0
дорівнює нулю. Але точка 0 не є точкою
перегину цієї функції. Це показує, що
не в кожній критичній точці 2 буде перегин
графіка функції. Отже і тут потрібні
достатні умови.
Теорема 2 (Достатні умови існування точок перегину).
Нехай
функція
![]() неперервна в
неперервна в
![]() і двічі диференційована в
і двічі диференційована в
![]() .
Тоді, якщо при проходженні через точку
.
Тоді, якщо при проходженні через точку
![]() друга похідна змінює знак, то ця точка
є точкою перегину функції, якщо ж при
проходженні друга похідна не змінює
знаку, то ця точка
друга похідна змінює знак, то ця точка
є точкою перегину функції, якщо ж при
проходженні друга похідна не змінює
знаку, то ця точка
![]() не є точкою перегину.
не є точкою перегину.
Доведення.
Нехай,
наприклад, в лівому півоколі похідна
додатня, а в правому – менша нуля. Звідси,
за теоремою про опуклість-вгнутість,
матимемо, що в лівому півоколі графік
вгнутий, а в правому – опуклий. Тобто,
бачимо, що з різних боків точки
![]() графік має різні опуклості, а це за
означенням значить, що точка
графік має різні опуклості, а це за
означенням значить, що точка
![]() є точкою перегину. Якщо ж друга похідна
при проходженні через точку
є точкою перегину. Якщо ж друга похідна
при проходженні через точку
![]() не змінює знак, то одержуємо «однакову
опуклість», а отже точка
не змінює знак, то одержуємо «однакову
опуклість», а отже точка
![]() не є точкою перегину.
не є точкою перегину.
Теорема доведена.
З попередніх двох теорем випливає наступний алгоритм пошуку точок перегину.
1. Знаходимо похідну ІІ порядку.
2. Знаходимо критичні точки 2.
3. До кожної із точок, одержаних в пункті 2) застосовуємо тільки що доведену теорему.
3. 2. 5. Асимптоти графіка функції
Означення
1.
Пряма
![]() називається вертикальною
асимптотою графіку
функції
називається вертикальною
асимптотою графіку
функції
![]() ,
якщо при
,
якщо при
![]() ,
маємо, що
,
маємо, що
![]() .
(Інколи прямування
.
(Інколи прямування
![]() слід брати тільки з однієї сторони).
слід брати тільки з однієї сторони).
Зауважимо,
що якщо пряма
![]() є вертикальною асимптотою, то в точці
є вертикальною асимптотою, то в точці
![]() функція
терпить розрив ІІ роду. Проте обернене
твердження невірне.
функція
терпить розрив ІІ роду. Проте обернене
твердження невірне.
Означення
2.
Пряма
![]() називається похилою
асимптотою
графіка функції
називається похилою
асимптотою
графіка функції
![]() на
на
![]() ,
якщо
,
якщо
![]() ,
коли
,
коли
![]() (
(![]() ).
).
Наступна теорема повністю вирішує проблему асимптот.
Теорема 1 (Критерій існування похилої асимптоти).
Для
того, щоб пряма
![]() була асимптотою
була асимптотою
![]() на
на
![]() (чи
(чи
![]() ,
чи
,
чи
![]() )
необхідно і достатньо, щоб існували
наступні границі і виконувалися наступні
рівності:
)
необхідно і достатньо, щоб існували
наступні границі і виконувалися наступні
рівності:
![]() (1)
(1)
![]() (2)
(2)
(на
![]() беруться коли
беруться коли
![]() ,
на
,
на
![]() ,
коли
,
коли
![]() ).
).
Доведення.
Необхідність.
Нехай
![]() є асимптотою
є асимптотою
![]() .
Це означає, що
.
Це означає, що
![]() (3)
(3)
З останньої рівності маємо
![]()
![]()
Ясно,
що права частина останньої рівності
при
![]() ,
,
![]() .
Отже, маємо, що
.
Отже, маємо, що
![]()
З
цієї ж самої рівності:
![]() .
Перейшовши до границі при
.
Перейшовши до границі при
![]() ,
,
![]() ,
одержуємо рівність (2).
,
одержуємо рівність (2).
Достатність.
Нехай тепер виконуються рівності (1) і (2). З рівності (2) будемо мати, що
![]()
Позначимо
різницю через
![]() .
Тоді, переписавши
.
Тоді, переписавши
![]()
одержимо,
що
![]() ,
(де
,
(де
![]() і
і
![]() визначаються рівностями (1) і (2)) є
асимптотою графіка.
визначаються рівностями (1) і (2)) є
асимптотою графіка.
Теорема доведена.
Повернемося на закінчення ще раз до дослідження функції на екстремум. Там в нас була теорема, яка дозволяє із критичних точок відбирати екстремальні. Виявляється є ще одна теорема, яка вирішує проблему, хоча іншими засобами.
Теорема 2 (ІІ достатні умови існування екстремуму).
Нехай
![]() – критична точка функції
– критична точка функції
![]() і ця функція двічі диференційована в
цій точці, якщо
і ця функція двічі диференційована в
цій точці, якщо
![]() ,
то
,
то
![]() – точка максимуму, якщо
– точка максимуму, якщо
![]() ,
то
,
то
![]() – точка мінімуму, якщо
– точка мінімуму, якщо
![]() – потрібно робити додаткові дослідження.
– потрібно робити додаткові дослідження.
Зауважимо, що сфера застосування цієї теореми вужча ніж першої .
Доведення.
В
такому виді таку теорему довести складно.
Доведення спроститься якщо покласти
додаткову вимогу, щоб
![]() існувала в деякому околі точки
існувала в деякому околі точки
![]() ,
і щоб
,
і щоб
![]() в точці
в точці
![]() була неперервною.
була неперервною.
Нехай
для конкретності
![]() в
деякому околі точки
в
деякому околі точки
![]() (теорема про консервативність). Тоді
(теорема про консервативність). Тоді
![]() в цьому околі спадна. Оскільки
в цьому околі спадна. Оскільки
![]() ,
то зліва від точки
,
то зліва від точки
![]()
![]() буде
буде
![]() ,
а справа –
,
а справа –
![]() .
А це означає, що
.
А це означає, що
![]() при переході через точку
при переході через точку
![]() змінює знак з «+» на «-». А це за першою
теоремо означає, що
змінює знак з «+» на «-». А це за першою
теоремо означає, що
![]() – точка максимуму.
– точка максимуму.
Теорема доведена.
Тепер «зберемо» все те, що ми зробили в якийсь алгоритм, який дозволить нам провести дослідження функції і побудувати її графік.
Схема дослідження функції і побудова її графіку.
Знаходимо область визначення функції.
З’ясовуємо, чи дана функція на цій області визначення є парна, непарна, періодична.
Встановлюємо точки розриву, проміжки неперервності функції. Встановлюємо існування вертикальних і похилих асимптот.
Знаходимо проміжки монотонності і точки екстремуму функції.
Знаходимо проміжки опуклості, вгнутості та точки перегину.
Якщо можливо, знаходимо точки перетину з осями координат.
Будуємо графік функції.
Наприклад.
Провести повне дослідження і побудувати графік функції
![]()
![]() .
.
Область визначення:
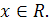

![]() ;
;![]() .
.
Неперервна на
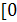 ;
;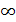 ).
).
Точок розриву, а отже, вертикальних асимптот немає.
З’ясуємо, чи є похилі асимптоти. Для цього шукаємо
![]()
![]()
![]()
![]() = 0;
= 0;
Отже
![]() .
Тому
.
Тому ![]() –
похила горизонтальна асимптота.
–
похила горизонтальна асимптота.
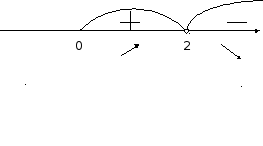
Знайдемо проміжки монотонності і точки екстремуму функції.
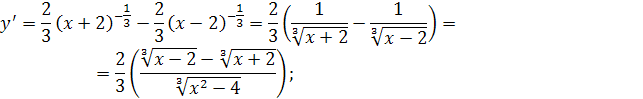

![]()
![]()
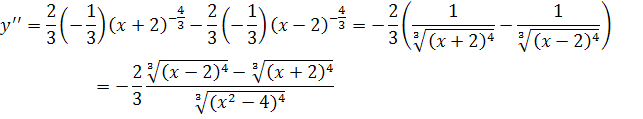
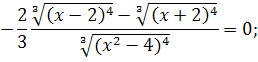
![]()
5.
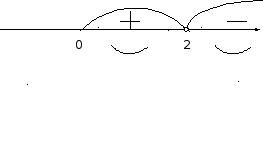
![]()
Будуємо графік
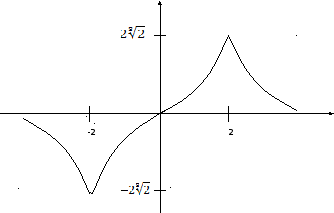
РОЗДІЛ IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
