2. 2. 3. Поняття підпослідовності. Теорема Больцано-Вейєрштрасса. Поняття часткової границі. Верхні і нижні границі, проблема їх існування

Знову розглянемо обмежені послідовності. Раніше ми довели, що із збіжності послідовності випливає її обмеженість, проте навпаки невірно. Наступна теорема дещо більше нам говорить про взаємозв’язок обмеженості і збіжності послідовності.

Нехай - деяка монотонно зростаюча послідовність натуральних чисел, а- послідовність дійсних чисел. Тоді послідовністьназивається підпослідовністю послідовності

Наприклад є підпослідовністю послідовностіОчевидно, що

Теорема 1(Больцано-Вейєрштрасса). З кожної обмеженої послідовності дійсних чисел можна виділити збіжну підпослідовність.

Доведення. Нехай - обмежена послідовність, тодіТочкоювідрізокподілимо на два рівних відрізки і позначимо черезтой із них, який містить безліч членів нашої послідовності (якщо цю властивість мають обидва відрізки, то беремо будь-який з них). Продовжуючи цей процес, ми одержуємо послідовність відрізків з такими властивостями:

1. 

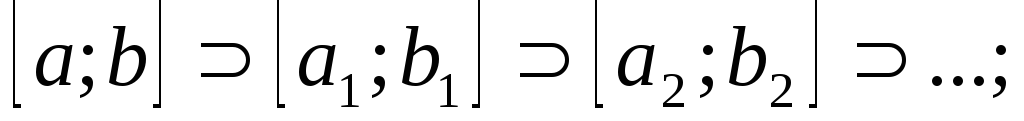
2. довжина відрізка 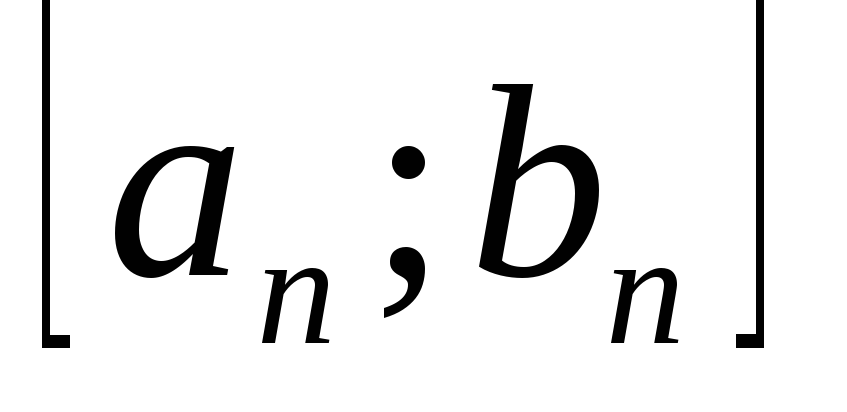дорівнює

3) містить безліч членів послідовності

Із властивостей 1) і 2) за аксіомою Кантора маємо, що

З’ясуємо далі скільки членів послідовності лежатиме в довільному околі точки Візьмемоі розглянемоЯк і при доведенні попередньої теореми завжди знайдетьсяі тоді з властивості 3) маємо, що вє безліч членів послідовності

Візьмемо і розглянемоЗа тільки що доведеним тут є члени нашої послідовностіВізьмемо один із них і позначимо його черезТодіабо

Візьмемо і розглянемоТоді існує член послідовності(який позначимо через) такий, що(такийобов’язково знайдеться, бо вє безліч членів нашої послідовності), причомуПродовжуючи цей процес і так далі, ми на- кроці візьмемоі розглянемоВ ньому знайдемотаке, що(1) і т. д..

Таким чином ми одержимо підпослідовність послідовностітаку, щоЗ останньої нерівності за теоремою „Про два міліціонери” одержимо, щоОтже, ми з послідовностівиділили збіжну послідовність. Теорема доведена.

Прості приклади показують , що умова обмеженості суттєва. Що стосується необмеженої послідовності то тут справедлива така

Теорема 2. Із кожної необмеженої послідовності можна виділити нескінченно-велику послідовність.

Пропонуємо читачу довести це твердження самостійно.

Число яке ми одержали в теоремі Больцано-Вейєрштрасса як границю деякої підпослідовності (і яке не зобов’язане бути границею послідовності), називатимемо частковою границею послідовності

Наприклад. Послідовність має дві часткові границі 0 і 1.

В зв’язку з введеним тільки-що поняттям часткової границі пропонуємо читачу довести ще одне твердження.

Теорема 3. Для того щоб обмежена послідовність була збіжною необхідно і достатньо, щоб вона мала одну часткову границю.

Очевидно, що обмежена послідовність може мати декілька і навіть безліч часткових границь (придумайте такі послідовності). Тому поставимо питання про найбільшу і найменшу з часткових границь даної послідовності. Першу з них називають верхньою, а другу – нижньою границями послідовності і позначають відповідно:і

Наприклад. Туті

Оскільки послідовність може мати безліч часткових границь, то виникає проблема існування нижніх і верхніх границь послідовності, бо не завжди із безлічі чисел можна знайти найменше і найбільше . Наступна теорема вирішує цю проблему.

Теорема 4 (про існування верхньої і нижньої границь послідовності).

Якщо обмежена послідовність, то існує її верхня і нижня границя.

Доведення. Нехай множина всіх часткових границь послідовностіОчевидно, ця множина не порожня (з теореми Больцано-Вейєрштрасса). Крім цього, вона ще й обмеженою. Справді, для будь-якої підпослідовностісправедлива нерівністьа звідси випливає, щоє нижньою межею множиниа- верхньою (за теоремою про граничний перехід в нерівностях).Тоді за відомою теоремою існуютьі

Для того, щоб закінчити доведення нашої теореми, достатньо довести , що іналежать множиніЦим самим буде показано, щоє найменшою частковою границею послідовностіанайбільшою.

Покажемо, що Для цього скористаємося тим, щоі за властивостями інфінуму матимемо,

1)

2) або записавши разом ці властивості –

Таким чином, ми зараз довели, що в будь-якому є хоча б один елемент множиниабо що те саме часткова границящо в свою чергу означає, що існуєякий повністю лежатиме ва влежатимуть всі члени деякої підпослідовності, починаючи з певного номера. Оскільки всі вони є членамито ми довели наступне: в будь-якомує безліч членів послідовності. Тоді звідси, як і при доведенні теореми Больцано-Вейєрштрасса, одержуємо, що існує деяка підпослідовністьпослідовностіяка збіжна до. Отже,- часткова границя і томуОскількито- найменший із елементівтому - нижня границя послідовності. Інший випадок доводиться аналогічно, що пропонуємо зробити читачу самостійно, так само як спробувати теж самостійно довести наступне твердження, яке в якійсь мірі узагальнює раніше приведене твердження.

Теорема 5. Для того, щоб обмежена послідовність була збіжною необхідно і достатньо, щоб її верхня і нижня границі співпадали.

Далі, проаналізувавши поняття верхньої і нижньої границь послідовності легко виходимо на такі властивості цих понять:

Якщо а то

1)

2)

3) всі члени послідовності, починаючи з деякого номера будуть належати відрізку