Властивість транзитивності

якщо іто

Доведемо це. Нехай маємо монотонно-неспадні і обмежені зверху послідовності чисел , які відповідно збігаються до чиселТе, щоозначає: Тоді

(1)

З того, що маємо:

і (2)

З (1) і (2) отримуємо, що А це означає, що послідовністьне мажорує послідовністьі згідно з означенням

Додавання дійсних чисел

Візьмемо Тоді нехай і монотонно неспадні послідовності раціональних чисел, для яких іє границями. Розглянемо послідовність . Оскільки ітоЗ того, щовипливає, . А це означає, що послідовність є монотонно неспадною. Крім тогоЗначить- монотонно неспадна, обмежена зверху послідовність раціональних чисел, яка згідно із означенням визначає деяке дійсне число, яке ми і назвемо сумою двох дійсних чиселі

Для введеної дії додавання дійсних чисел, як і для інших чисел справедливі асоціативний та комутативний закони,

1)

2)

Доведемо, наприклад, другу властивість. Візьмемо Нехай маємо послідовності і , які визначають відповідно числа іДаліщо і треба було довести.

Асоціативний закон пропонуємо читачу довести самостійно.

Легко, також, перевірити, що .

Спосіб, який ми використали для введення операції додавання дійсних чисел не можемо використати для введення дії віднімання дійсних чисел, тому що різниця двох монотонно неспадних послідовностей не зобов’язана бути монотонно неспадною. Отже, для введення віднімання дійсних чисел слід використати якісь нові підходи.

Віднімання дійсних чисел.

Ідея, яка дозволить нам ввести операцію віднімання полягає в наступному:

1. побудувати монотонно спадну послідовність раціональних чисел (і обмежену знизу) , яка має своєю границею число

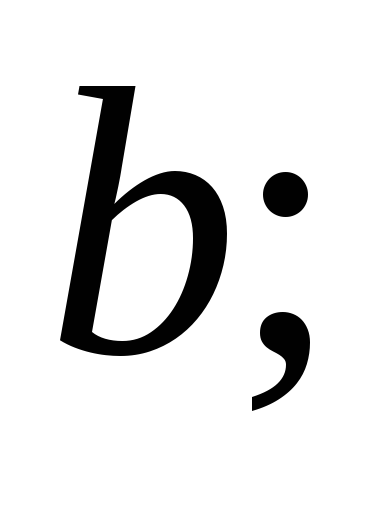
2. взяти послідовність 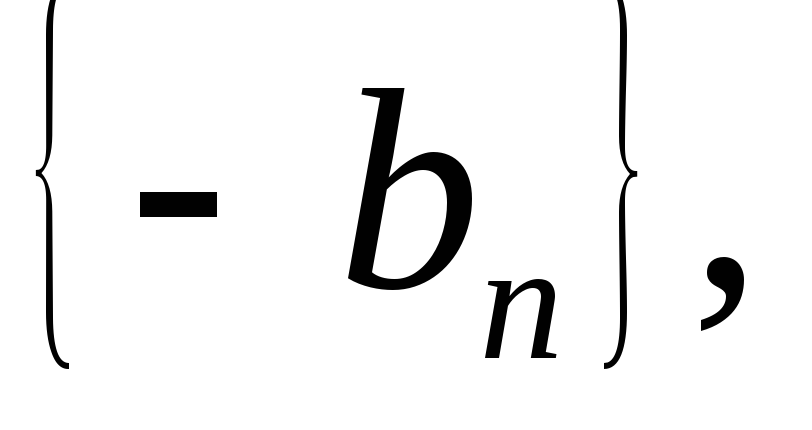яка буде монотонно зростаючою, обмеженою зверху та збіжною до числа

3. сума попередньої послідовності з послідовністю дасть монотонно неспадну і обмежену зверху послідовність, яка і визначатиме число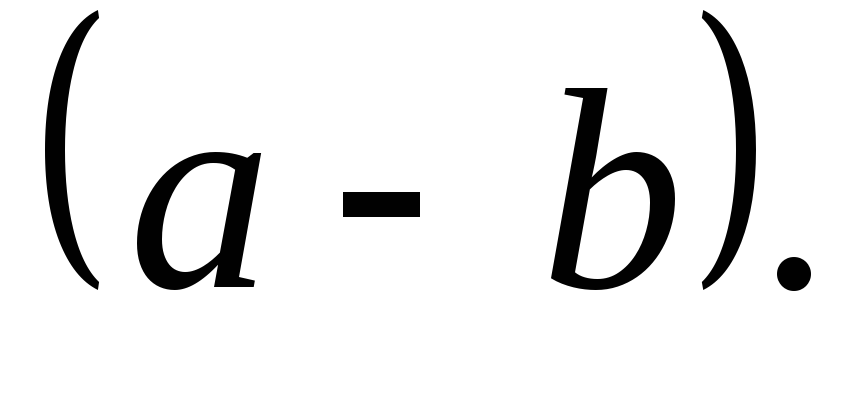

Почнемо реалізовувати цю ідею починаючи із такого твердження.

Теорема 1. (Про існування раціонального числа між будь-якими двома дійсними числами). Між будь-якими двома дійсними числами завжди існує раціональне число, тобто

Доведення. Нехай і - послідовності, що визначають дійсні числа і відповідно. З того, щомаємо, щоне мажорує . А це означає:

(1)

Оскільки в нерівності (1) є деяке стале конкретне число, а- пробігає всі натуральні числа імає своєю границею числото на основі цього з нерівності (1) за теоремою про граничний перехід в нерівностях матимемо:

(2)

Можна вважати, що послідовність не є стаціонарною (тобто така, що немає в ній члена починаючи з якого всі наступні, після нього, будуть рівні між собою. Якщо послідовністьє стаціонарною, то вона обов’язково задаватиме деяке раціональне числоі ми її замінимо іншою послідовністюяка буде монотонно зростаюча і також матиме своєю границею число). Тому існує номертакий, що. Звідси будемо мати:(3). Знайдемо ще одне(4). Число- раціональне:. Порівняємо його з числом(як порівнюються дійсні числа). Задамо числопослідовністю (як дійсне число):числотакож задамо послідовністю:яка утворена з послідовностівилученнямчленів (така процедура на збіжність і границю не впливає). Оскільки будь-який член другої послідовності не менший за будь-який член першої послідовності, то зразу бачимо, що перша послідовність не мажорує другу. Тому за означенням матимемо, що:Звідси і з (4) отримаємо:А це разом з (3) означає, щоІ оскількиє числом раціональним, то воно може бути взяте в якості потрібного намТеорема доведена.

За допомогою цієї теореми вже можна реалізувати перший пункт оголошеної вище ідеї. Справедлива така

Теорема 2. Для будь-якого дійсного числа існує збіжна до нього, монотонно-спадна і обмежена знизу послідовність раціональних чисел.

Доведення. Розглянемо монотонно спадну послідовність дійсних чисел: Порівняємо сусідні числа:Тоді за теоремою 1 ми знайдемо числоВикористовуючи цю ж ідею отримаємо:і томуПродовжуючи цей процес на-му кроці ми знайдемоі на-му кроціі т. д. Звідси і попередньої нерівності отримаємо(*). Продовжуючи цей процес і так далі ми отримаємо послідовністьтаку, що:

1) всі її члени є раціональні числа;

2) ця послідовність є монотонно спадною;

3) а це означає, що знайдена послідовність є обмеженою зверху.

Для того, щоб показати, що ця послідовність збіжна до числа потрібно використати наступну нерівність:і застосувати теорему „про два міліціонери”. Оскільки зліва і справа є збіжні до числапослідовності, тощо і треба було довести.

Тепер вже легко можемо ввести операцію віднімання на множині дійсних чисел. Візьмемо дві послідовності раціональних чисел і : перша з них монотонно неспадна і обмежена зверху, а друга монотонно спадна і обмежена знизу, які збіжні відповідно до дійсних чисел і

Розглянемо Неважко показати, що ця послідовність є монотонно неспадною і обмеженою зверху. Значить остання послідовність визначає деяке дійсне число, яке логічно прийняти за різницю чиселіЗауважимо, що ми при введенні різниці одночасно зробили все потрібне і для того, щоб ввести поняття протилежного елемента,

Тепер вже можна ввести поняття модуля дійсного числа: