27 Применение дифференциала

Рассмотрим для примера функцию

от двух переменных, которую будем предполагать дифференцируемой.

Мы хотим вычислить эту функцию в точке , где

,

,

Приближенные значения этих чисел запишем в виде конечных десятичных дробей

,

.

Таким образом, имеют место приближенные равенства

с абсолютными погрешностями приближения, удовлетворяющими неравенствам

.

Подставив в функцию вместосоответственно, получим приближенное равенство

с абсолютной погрешностью

,

которую при достаточно малых можно приближенно заменить дифференциалом функциив точке:

.

Отсюда получаем неравенство

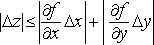.                               (1)

На самом деле это неравенство приближенное, потому что мы получили его, пренебрегая некоторой величиной, правда, значительно меньшей, чем .

Обратим внимание на тот факт, что конечные десятичные дроби при уменьшении,становятся все более и более громоздкими. Поэтому при вычислении числамы должны беспокоиться не только о том, чтобы оно приближалодолжным образом, но и чтобы производимые при этом вычисления совершались возможно, экономно. В силу этого замечания из неравенства (1) следует, что если нужно, чтобы абсолютная погрешностьне превышала данную малую величину, которую мы обозначим через, то этого мы достигнем, взяв числа,такими, чтобы выполнялись неравенства

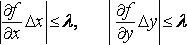,                       (2)

т. е. чтобы погрешность распределялась между слагаемыми в правой части неравенства (1) поровну.

Из неравенств (2) видно, что вычисления будут наиболее экономными, если в качестве ,(на самом деле,) взять наибольшие возможные числа, удовлетворяющие этим неравенствам.

П р и м е р  1. Функция имеет для,непрерывные частные производные, равные

.

Поэтому приближенное равенство

имеет абсолютную погрешность, которая при малых приращениях , если пренебречь величинами, значительно меньшими этих приращений, удовлетворяет неравенству

.

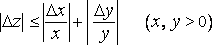Если требуется, чтобы гарантированная погрешность была меньше , надо подобратьтак, чтобы

.

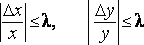Мы видим, что числа не обязательно должны быть равными. Если, например,значительно меньше, чем, то соответственно надо взятьменьшим, чем. Иначе наши вычисления были бы неэкономными. Если бы, например, было, что

,

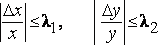где , то оказалось бы, что

,

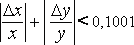и при этом на вычисление второго слагаемого , ввиду излишней малости, мы потратили бы излишнюю работу. Между тем вычисления упростятся, если взять возможно большие,, удовлетворяющие неравенствам.

.

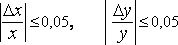П р и м е р  2. Функция имеет непрерывные частные производные,. Поэтому приближенное равенство

имеет абсолютную погрешность , которая при малых приращениях, если пренебречь величинами, значительно меньшими этих приращений, удовлетворяет соотношениям

.

Соответственно относительная погрешность удовлетворяет соотношениям

.

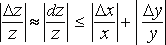Мы видим, что при малых иможно считать, что относительная погрешность произведения не превышает сумму относительных погрешностей сомножителей.

П р и м е р   3. Функция дляимеет непрерывные частные производные

.

Поэтому приближенное равенство

имеет абсолютную погрешность , которая при малых приращениях, если пренебречь величинами, значительно меньшими, чем, удовлетворяет соотношениям

.

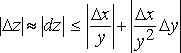Соответственно относительная погрешность удовлетворяет соотношениям

.

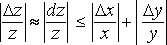Таким образом, при малых иможно считать, что относительная погрешность частного не превышает сумму относительных погрешностей делимого и делителя.