
- •2 Определители матриц
- •4 Координаты на прямой в плоскости и пространстве.Оси,направленные отрезки.
- •5 Векторы. Линейные операции над векторами, разложение вектора по базису
- •Линейные операции над векторами
- •Базис и разложение по базису
- •Обозначения
- •6 Скалярное,векторное и смешанное произведение векторов.
- •18 Основные правила нахождения производной
- •19 Применение производной к нахождению нибольших и наименьших значений функций на отрезке.
- •20 Функции 2 переменных. Частные производные. Перестановочность частных производных.Линии уровня.Градиент.
- •Способы задания функции
- •Непрерывность функции двух переменных
- •Основные свойства непрерывных функций двух переменных
- •21 Пределы и непрерывность функций 2 переменных. Особые точки
- •Особые точки векторных полей на плоскости
- •22 Двойные интегралы. Мин и Макс значение функции 2 переменных в области
- •25 Разложение в степенные ряды основных элементарных функций.Формула Моавра.
- •26 Дифференциал функции.
- •27 Применение дифференциала
- •29 Таблица основных неопределённых интегралов.
- •35 Элементы комбинаторики-перестановки,размещения, сочетания
- •Размещения, перестановки, сочетания
- •Свойства чисел
- •Треугольник Паскаля
- •36 Понятие случайного события, вероятность события.
- •0 Ј p(a) ј 1
- •37 Основные правила нахождения вероятности события.38,39
- •40 Схема Бернулли. Формула Пуасова. Локальная и интегральные формулы Моавра-Лапласа
- •41 Функция распределения. Закон распределения.
- •42 Корреляция. Вычисление коэффицициентов корреляции.
Базис и разложение по базису
![]()
Разложение вектора по трём ортогональным векторам трёхмерного евклидова пространства
Векторы (как направленные отрезки), лежащие на прямых, параллельныходной прямой, называютсяколлинеарными, а векторы, лежащие в плоскостях, параллельных однойплоскости—компланарными. Для свободных векторов коллинеарность и компланарность определяется как такие понятия для изображающих их направленных отрезков (то есть представителей соответствующих свободным векторам классов эквивалентности).
Каждый вектор плоскости можно единственным образом разложить по двум определённым неколлинеарным векторам этой плоскости, а каждый вектор трёхмерного евклидова пространства можно единственным образом разложить по трём определённым некомпланарным векторам. Эти векторы, взятые в определённом порядке называются базисом плоскости (пространства). Сопоставлением каждому вектору данной плоскости (пространства) его коэффициентов в таком его разложении, определяется аффинная система координатна плоскости (в пространстве). Если векторы, по которым производится разложение, ортогональны и единичны, то получаемпрямоугольную декартову систему координатна плоскости (в пространстве). Разложение геометрического вектора по базису есть упорядоченная совокупность проекций вектора на базисные вектора.
Обозначения
Вектор,
представленный набором
![]() элементов
(компонент)
элементов
(компонент)![]() допустимо
обозначить следующим способами:
допустимо
обозначить следующим способами:
![]() .
.
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
![]()
Сложение векторов почти всегда обозначается знаком плюс:
![]() .
.
Умножение на число — просто написанием рядом, без специального знака, например:
![]() ,
,
причём число при этом обычно пишут слева.
6 Скалярное,векторное и смешанное произведение векторов.
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Обычно используется одно из следующих обозначений:
![]() ,
,
![]() ,
,
![]() ,
,
или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):
![]() .
.
Обычно предполагается что скалярное произведение положительно определено, то есть
![]() для
всех
для
всех
![]() .
.
Если этого не предполагать, то произведение называется индефинитным.
Скалярным
произведением
в векторном
пространстве
![]() над
полем
над
полем![]() называется
функция
называется
функция![]() для
элементов
для
элементов![]() ,
принимающая значения в
,
принимающая значения в![]() ,
определенная для каждой пары элементов
и удовлетворяющая следующим условиям:
,
определенная для каждой пары элементов
и удовлетворяющая следующим условиям:
для любых трех элементов
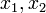 и
и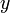 пространства
пространства
 и
любых чисел
и
любых чисел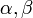 справедливо
равенство
справедливо
равенство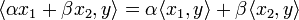 (линейность
скалярного произведения по первому
аргументу);
(линейность
скалярного произведения по первому
аргументу);для любых
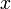 и
и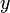 справедливо
равенство
справедливо
равенство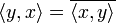 ,
где черта означает комплексное сопряжение
(эрмитова симметричность);
,
где черта означает комплексное сопряжение
(эрмитова симметричность);для любого
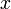 имеем
имеем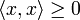 ,
причем
,
причем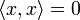 только
при
только
при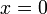 (положительная
определенность скалярного произведения).
(положительная
определенность скалярного произведения).
Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
Заметим,
что из п.2 определения следует, что
![]() действительное.
Поэтому п.3 имеет смысл несмотря на
комплексные (в общем случае) значенияскалярного
произведения.
действительное.
Поэтому п.3 имеет смысл несмотря на
комплексные (в общем случае) значенияскалярного
произведения.
Векторным
произведением
вектора
![]() на
вектор
на
вектор![]() в
пространстве
в
пространстве![]() называется
вектор
называется
вектор![]() ,
удовлетворяющий следующим требованиям:
,
удовлетворяющий следующим требованиям:
длина вектора
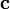 равна
произведению длин векторов
равна
произведению длин векторов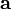 и
и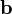 насинус
угла
насинус
угла
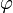 между
ними:
между
ними: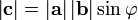 ;
;вектор
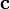 ортогонален
каждому из векторов
ортогонален
каждому из векторов
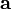 и
и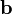 ;
;вектор
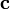 направлен
так, что тройка векторов
направлен
так, что тройка векторов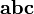 является
правой;
является
правой;в случае пространства
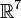 требуется
ассоциативность тройки векторов
требуется
ассоциативность тройки векторов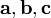 .
.
Обозначение:
![]()
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Сме́шанное
произведе́ние
![]() векторов
векторов
![]() —скалярное
произведение
вектора
—скалярное
произведение
вектора
![]() навекторное
произведение
векторов
навекторное
произведение
векторов
![]() и
и![]() :
:
![]() .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический
смысл:
Модуль смешанного произведения численно
равен объёму параллелепипеда,
образованного векторами
![]() .
.
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
![]()
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
![]()
Смешанное произведение
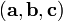 в
правой декартовой системе координат
(в ортонормированном базисе) равноопределителю
матрицы,
составленной из векторов
в
правой декартовой системе координат
(в ортонормированном базисе) равноопределителю
матрицы,
составленной из векторов
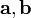 и
и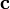 :
:
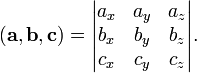
Смешанное произведение
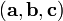 в
левой декартовой системе координат (в
ортонормированном базисе) равноопределителю
матрицы,
составленной из векторов
в
левой декартовой системе координат (в
ортонормированном базисе) равноопределителю
матрицы,
составленной из векторов
 и
и ,
взятому со знаком "минус":
,
взятому со знаком "минус":
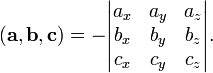
В частности,
Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
Геометрический смысл — Смешанное произведение
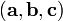 по
абсолютному значению равно объёмупараллелепипеда
(см. рисунок), образованного векторами
по
абсолютному значению равно объёмупараллелепипеда
(см. рисунок), образованного векторами
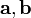 и
и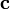 ;
знак зависит от того, является ли эта
тройка векторов правой или левой.
;
знак зависит от того, является ли эта
тройка векторов правой или левой.Квадрат смешанного произведения векторов равен определителю Грама, определяемому ими[1]:215.
![]()
Три вектора, определяющие параллелепипед.
Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
![]()
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).
