18 Основные правила нахождения производной

19 Применение производной к нахождению нибольших и наименьших значений функций на отрезке.

Достаточное условие возрастания функции

Если в каждой точке интервала (a, b) f'(x)>0, то функция  f(x) возрастает на этом интервале.

Достаточное условие убывания функции.

Если в каждой точке интервала (a, b) f'(x)<0, то функция  f(x) убывает на этом интервале.

Определение:

x₀ называется критической точкой функции  f(x), если

1) x₀ – внутренняя точка области определения  f(x) ;

2) f'(x₀)=0 или f'(x₀) не существует.

Необходимое условие экстремума:

Если x₀– точка экстремума функции  f(x), то эта точка является критической точкой данной функции.

Достаточное условие экстремума:

Если при переходе через точку x₀ производная функции меняет знак, то x₀ – точка экстремума функции  f(x).

Примеры экстремумов:

Схема исследования функции.

1. Найти область определения функции.

2. Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.

3. Найти, если это возможно, точки пересечения графика функции с осями координат и промежутки знакопостоянства функции. Иногда для уточнения построения графика следует найти две три дополнительные точки.

4. Найти производную функции и ее критические точки.

5. Найти промежутки монотонности и экстремумы функции.

6. Построить график функции, используя полученные результаты исследования.

Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].

1. Найти значения функции в концах отрезка, т.е. f(a) и f(b) ;

2. Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b) ;

3. Из найденных значений выбрать наибольшее и наименьшее.

20 Функции 2 переменных. Частные производные. Перестановочность частных производных.Линии уровня.Градиент.

В естествознании встречаются ситуации, когда одна величина является функцией нескольких других:

,

- работа тока на участке цепи и др.

Далее остановимся на случае функции 2 переменных.

 

Определение 25.1.

Если каждой паре (x,y) значений двух, независимых друг от друга, переменных величин x и y , из некоторой области их изменений D,  соответствует одно определенное значение величины z, то говорят, что z – есть функция двух независимых переменных  x и y , определенная  в области D (область определения функции).

Обозначение: z = f(x,y)=g(x,y)…

 

Способы задания функции

Табличный

S=S(x,y)

yx	1	1.5	2
1	1	1.5	2
5	5	7.5	10

 

 

 

Аналитическое задание функции

.

 

Определение 25.2.

Областью определения функции z = f(x,y) называется множество {x,y}, для которых формула имеет смысл.

 

Пример 25.1.

Функция определена при.

 

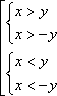Графическое задание функции.

 

Определение 25.3.

Пусть задана функция Графиком называется множество точек в пространстве , где-абсцисса,- ордината, а- аппликата, т.е. графиком являетсяповерхность.

 

Ранее изучали, что - верхняя часть сферы,

- параболоид, - плоскость.

 

Замечание 1. Любая поверхность в пространстве является графиком функции, если прямая, параллельная, пересекает ее в одной точке.

 

Предел функции двух переменных

 

Определение 25.4.

Множество точек , удовлетворяющих неравенству

называется -окрестностью точки.

Геометрический смысл

-окрестность точки - круг с центром в точкерадиуса.

 

Определение 25.5.

Функция имеет предел в точкеравный, т.е.

,

если она определена в некоторой окрестности точки , и для любого сколь угодно малогонайдется такое, что для всех точек, удовлетворяющих неравенствувыполняется неравенство

.

 

Замечание 2. Все правила нахождения пределов, сформулированные для функции одной переменной остаются в силе и для функции двух переменных.

 

Пример 25.2.

1) ,

2) .

 

Пусть

Определение 25.6.

Функция называетсябесконечно малой в точке

(или при ), если.

Если , то, где,

т.е. функция в окрестности точкиотличается от числана бесконечно малую функцию.

 

Замечание 3.

Сравнение бесконечно малых функций двух переменных производится также, как и бесконечно малых функций одной переменной, причем под символом будем понимать любую бесконечно малую в точкефункцию более высокого порядка малости, чем бесконечно малая в точкефункция, т.е..