
- •2 Определители матриц
- •4 Координаты на прямой в плоскости и пространстве.Оси,направленные отрезки.
- •5 Векторы. Линейные операции над векторами, разложение вектора по базису
- •Линейные операции над векторами
- •Базис и разложение по базису
- •Обозначения
- •6 Скалярное,векторное и смешанное произведение векторов.
- •18 Основные правила нахождения производной
- •19 Применение производной к нахождению нибольших и наименьших значений функций на отрезке.
- •20 Функции 2 переменных. Частные производные. Перестановочность частных производных.Линии уровня.Градиент.
- •Способы задания функции
- •Непрерывность функции двух переменных
- •Основные свойства непрерывных функций двух переменных
- •21 Пределы и непрерывность функций 2 переменных. Особые точки
- •Особые точки векторных полей на плоскости
- •22 Двойные интегралы. Мин и Макс значение функции 2 переменных в области
- •25 Разложение в степенные ряды основных элементарных функций.Формула Моавра.
- •26 Дифференциал функции.
- •27 Применение дифференциала
- •29 Таблица основных неопределённых интегралов.
- •35 Элементы комбинаторики-перестановки,размещения, сочетания
- •Размещения, перестановки, сочетания
- •Свойства чисел
- •Треугольник Паскаля
- •36 Понятие случайного события, вероятность события.
- •0 Ј p(a) ј 1
- •37 Основные правила нахождения вероятности события.38,39
- •40 Схема Бернулли. Формула Пуасова. Локальная и интегральные формулы Моавра-Лапласа
- •41 Функция распределения. Закон распределения.
- •42 Корреляция. Вычисление коэффицициентов корреляции.
25 Разложение в степенные ряды основных элементарных функций.Формула Моавра.
Из дифференциального исчисления известно, что если функция f(x) имеет в некоторой окрестности производные до порядка n включительно, то можно написать формулу Тейлора для этой функции. Положим при любом n = 1, 2,…
![]()
и
![]() Если
Если
![]() (1.1)
(1.1)
то ряд
![]()
сходится и его суммой будет функция f(x).
Определение 1.1. Представление функции f(x) в виде ряда
![]() (1.2)
(1.2)
называется разложением этой функции в ряд Тейлора.
Определение 1.2. Разложение функции f(x) в ряд Тейлора при x0=0
![]() (1.3)
(1.3)
называется разложением этой функции в ряд Маклорена.
Подчеркнем, что из сходимости ряда Тейлора для функции f(x) еще не следует его сходимость именно к этой функции, поэтому при разложении функции в ряд Тейлора следует проверять соблюдение условия (1.1).
Теорема 1.1. Пусть
![]() (1.4)
где
стоящий справа ряд сходится в некотором
отрезке
(1.4)
где
стоящий справа ряд сходится в некотором
отрезке
![]() к
функцииf(x).
Тогда этот ряд является рядом Тейлора,
то есть
к
функцииf(x).
Тогда этот ряд является рядом Тейлора,
то есть
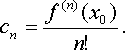 (1.5)
(1.5)
Доказательство. Применим к равенству (1.4) п раз теорему о почленном дифференцировании степенного ряда. Тогда получим
![]()
Если
в этом тождестве положить x=x0
,
то все слагаемые справа, кроме первого,
обратятся в нуль и получим
![]() откуда и следует (1.5). Теорема доказана.
откуда и следует (1.5). Теорема доказана.
2. Разложение основных элементарных функций.
Теорема
2.1. Если
функция f(x)
определена и
имеет
производные сколь угодно высоких
порядков и существует постоянная,
такая, что при любых
х и п удовлетворяет неравенству
![]() то
функция f(x)
разлагается
в ряд Тейлора (1.2) при любом x0.
то
функция f(x)
разлагается
в ряд Тейлора (1.2) при любом x0.
Приведем без доказательства следующие разложения элементарных функций в ряд Маклорена
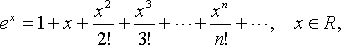
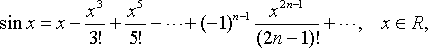
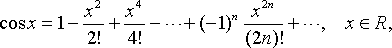
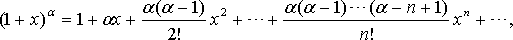
это
разложение имеет место при любом
натуральном значении
![]() и
любом значенииx,
если число
и
любом значенииx,
если число
![]() не
является натуральным, то данное равенство
справедливо лишь при –1<x<1;
не
является натуральным, то данное равенство
справедливо лишь при –1<x<1;
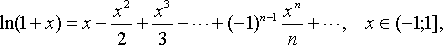
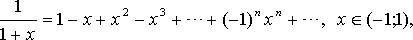
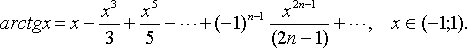
Формула
Муавра
для комплексных чисел
![]() утверждает,
что
утверждает,
что
![]()
для
любого
![]()
Формула
Муавра сразу следует из формулы
Эйлера
![]() и
тождества дляэкспонент
и
тождества дляэкспонент
![]() ,
гдеb
— целое
число.[1]
,
гдеb
— целое
число.[1]
Аналогичная
формула применима также и при вычислении
корней n-ой
степени из ненулевого комплексного
числа: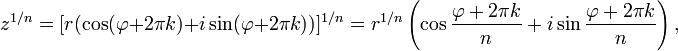
где k = 0, 1, …, n—1.
Из
основной
теоремы алгебры
следует, что корни n-й
степени из комплексного числа всегда
существуют, и их количество равно n.
На комплексной плоскости, как видно из
формулы, все эти корни являются вершинами
правильного
n-угольника,
вписанного в окружность
радиуса
![]() с
центром в нуле.
с
центром в нуле.
26 Дифференциал функции.
Итак,
график дифференцируемой функции в
окрестности каждой своей точки сколь
угодно близко приближается к графику
касательной в силу равенства:
![]() где
α – бесконечно малая в окрестности
где
α – бесконечно малая в окрестности![]() функция.
Для приближенного вычисления значения
функции f в точке x0 + Δx
эту бесконечно малую функцию можно
отбросить:
функция.
Для приближенного вычисления значения
функции f в точке x0 + Δx
эту бесконечно малую функцию можно
отбросить:
|
|
Линейную
функцию
![]() называют
дифференциалом функции f в точке
называют
дифференциалом функции f в точке![]() и
обозначают df. Для функции x производная
в каждой точке
и
обозначают df. Для функции x производная
в каждой точке![]() равна 1,
то есть
равна 1,
то есть![]() Поэтому
пишут:
Поэтому
пишут:
|
Приближенное
значение функции вблизи точки
![]() равно
сумме ее значения в этой точке и
дифференциала в этой же точке. Это дает
возможность записать производную
следующим образом:
равно
сумме ее значения в этой точке и
дифференциала в этой же точке. Это дает
возможность записать производную
следующим образом:
|
|
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
