
- •2 Определители матриц
- •4 Координаты на прямой в плоскости и пространстве.Оси,направленные отрезки.
- •5 Векторы. Линейные операции над векторами, разложение вектора по базису
- •Линейные операции над векторами
- •Базис и разложение по базису
- •Обозначения
- •6 Скалярное,векторное и смешанное произведение векторов.
- •18 Основные правила нахождения производной
- •19 Применение производной к нахождению нибольших и наименьших значений функций на отрезке.
- •20 Функции 2 переменных. Частные производные. Перестановочность частных производных.Линии уровня.Градиент.
- •Способы задания функции
- •Непрерывность функции двух переменных
- •Основные свойства непрерывных функций двух переменных
- •21 Пределы и непрерывность функций 2 переменных. Особые точки
- •Особые точки векторных полей на плоскости
- •22 Двойные интегралы. Мин и Макс значение функции 2 переменных в области
- •25 Разложение в степенные ряды основных элементарных функций.Формула Моавра.
- •26 Дифференциал функции.
- •27 Применение дифференциала
- •29 Таблица основных неопределённых интегралов.
- •35 Элементы комбинаторики-перестановки,размещения, сочетания
- •Размещения, перестановки, сочетания
- •Свойства чисел
- •Треугольник Паскаля
- •36 Понятие случайного события, вероятность события.
- •0 Ј p(a) ј 1
- •37 Основные правила нахождения вероятности события.38,39
- •40 Схема Бернулли. Формула Пуасова. Локальная и интегральные формулы Моавра-Лапласа
- •41 Функция распределения. Закон распределения.
- •42 Корреляция. Вычисление коэффицициентов корреляции.
4 Координаты на прямой в плоскости и пространстве.Оси,направленные отрезки.
Расстояние d между точками A(x1) и B(x2) на оси:
![]()
![]()
![]()
![]()
![]()
Величина AB (алгебраическая) направленного отрезка на оси:
AB = x2 - x1.
Если известны координаты концов отрезка прямой, то тем самым положение отрезка на плоскости вполне определено. Координаты точки записываются в скобках рядом с названием точки, причем всегда на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором - ее ордината. Например, если x1 - абсцисса точки A, а y1 - ее ордината, то это записывается так: A(x1, y1).
У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты начала координат равны нулю.
Расстояние d между точками A(x1, y1) и B(x2, y2) плоскости определяется по формуле:
![]()
![]()
![]()
Проекции
на оси координат направленного отрезка,
или вектора
![]() на
плоскости с началомA(x1,
y1)
и концом B(x2,
y2):
на
плоскости с началомA(x1,
y1)
и концом B(x2,
y2):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тангенс угла между отрезком и положительным направлением оси Ox определяется по формуле (этот угол отсчитывается от оси Ox против часовой стрелки):
![]()
![]()
![]()
![]()
![]()
Определенный
по этой формуле
![]()
![]() является
угловым коэффициентом прямой.
является
угловым коэффициентом прямой.
Прямоугольная система координат на плоскости
Прямоугольная
система координат на плоскости образуется
двумя взаимно перпендикулярными осями
координат
![]() и
и![]() .
Оси координат пересекаются в точке
.
Оси координат пересекаются в точке![]() ,
которая называетсяначалом
координат,
на каждой оси выбрано положительное
направление.
,
которая называетсяначалом
координат,
на каждой оси выбрано положительное
направление.
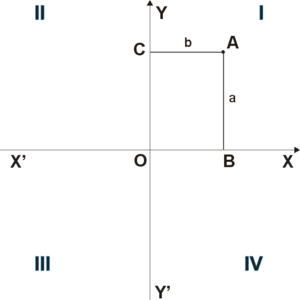
![]()
Рис. 1
Положение
точки
![]() на
плоскости определяется двумя координатами
на
плоскости определяется двумя координатами![]() и
и![]() .
Координата
.
Координата![]() равна
длине отрезка
равна
длине отрезка![]() ,
координата
,
координата![]() —
длине отрезка
—
длине отрезка![]() в
выбранных единицах измерения. Отрезки
в
выбранных единицах измерения. Отрезки![]() и
и![]() определяются
линиями, проведёнными из точки
определяются
линиями, проведёнными из точки![]() параллельно
осям
параллельно
осям![]() и
и![]() соответственно.
соответственно.
При
этом координате
![]() приписывается
знак минус, если точка
приписывается
знак минус, если точка![]() лежит
на луче
лежит
на луче![]() (а
не на луче
(а
не на луче![]() ,
как на рисунке). Координате
,
как на рисунке). Координате![]() приписывается
знак минус, если точка
приписывается
знак минус, если точка![]() лежит
на луче
лежит
на луче![]() .
Таким образом,
.
Таким образом,![]() и
и![]() являются
отрицательными направлениями осей
координат (каждая ось координат
рассматривается какчисловая
ось).
являются
отрицательными направлениями осей
координат (каждая ось координат
рассматривается какчисловая
ось).
Координата
![]() называетсяабсциссой
точки
называетсяабсциссой
точки
![]() ,
координата
,
координата![]() —ординатой
точки
—ординатой
точки
![]() .
.
Символически это записывают так:
![]()
или
![]()
или указывают принадлежность координат конкретной точке с помощью индекса:
![]()
итд.
В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси
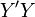 вверх,
ось
вверх,
ось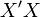 смотрела
направо. Обычно принято пользоваться
правосторонними системами координат
(если обратное не оговорено или не
очевидно - например, их чертежа; иногда
по каким-то соображениям бывает удобнее
всё же пользоватьсялевосторонней
системой координат).
смотрела
направо. Обычно принято пользоваться
правосторонними системами координат
(если обратное не оговорено или не
очевидно - например, их чертежа; иногда
по каким-то соображениям бывает удобнее
всё же пользоватьсялевосторонней
системой координат).
Четыре угла (I, II, III, IV), образованные осями координат
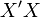 и
и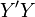 ,
называются координатными углами иликвадрантами
(см. рис. 1).
,
называются координатными углами иликвадрантами
(см. рис. 1).
Если точка
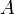 лежит
в координатном углу I, то точка
лежит
в координатном углу I, то точка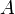 имеет
положительные абсциссу и ординату.
Если точка
имеет
положительные абсциссу и ординату.
Если точка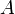 лежит
в координатном углу II, то точка
лежит
в координатном углу II, то точка имеет
отрицательную абсциссу и положительную
ординату. Если точка
имеет
отрицательную абсциссу и положительную
ординату. Если точка лежит
в координатном углу III, то точка
лежит
в координатном углу III, то точка имеет
отрицательные абсциссу и ординату.
Если точка
имеет
отрицательные абсциссу и ординату.
Если точка лежит
в координатном углу IV, то точка
лежит
в координатном углу IV, то точка имеет
положительную абсциссу и отрицательную
ординату.
имеет
положительную абсциссу и отрицательную
ординату.Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трехмерное пространство, о более многомерных пространствах - см. ниже) образуется тремя взаимно перпендикулярными осями координат
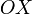 ,
,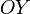 и
и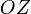 .
Оси координат пересекаются в точке
.
Оси координат пересекаются в точке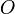 ,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно (не обязательно[2])
одинаковы для всех осей.
,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно (не обязательно[2])
одинаковы для всех осей.
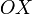 —ось
абсцисс,
—ось
абсцисс,
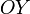 —ось
ординат,
—ось
ординат,
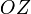 —ось
аппликат.
—ось
аппликат.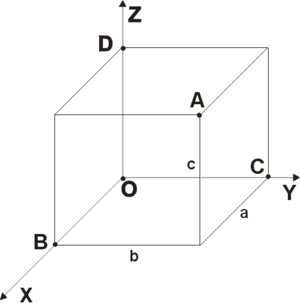

Рис. 2
Положение точки
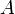 в
пространстве определяется тремя
координатами
в
пространстве определяется тремя
координатами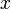 ,
,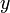 и
и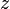 .
Координата
.
Координата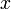 равна
длине отрезка
равна
длине отрезка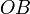 ,
координата
,
координата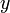 —
длине отрезка
—
длине отрезка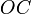 ,
координата
,
координата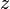 —
длине отрезка
—
длине отрезка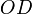 в
выбранных единицах измерения. Отрезки
в
выбранных единицах измерения. Отрезки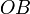 ,
,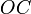 и
и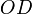 определяются
плоскостями, проведёнными из точки
определяются
плоскостями, проведёнными из точки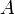 параллельно
плоскостям
параллельно
плоскостям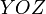 ,
,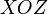 и
и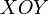 соответственно.
соответственно.Координата
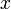 называется
абсциссой точки
называется
абсциссой точки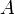 ,
,координата
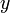 —
ординатой точки
—
ординатой точки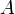 ,
,координата
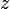 —аппликатой
точки
—аппликатой
точки
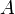 .
.Символически это записывают так:
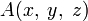
или
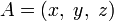
или привязывают запись координат к конкретной точке с помощью индекса:
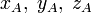
итп.
Каждая ось рассматривается как числовая прямая, т.е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка
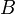 лежала
не как на рисунке - на луче
лежала
не как на рисунке - на луче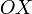 ,
а на его продолжении в обратную сторону
от точки
,
а на его продолжении в обратную сторону
от точки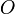 (на
отрицательной части оси
(на
отрицательной части оси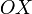 ),
то абсцисса
),
то абсцисса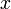 точки
точки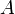 была
бы отрицательной (минус расстоянию
была
бы отрицательной (минус расстоянию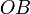 ).
Аналогично и для двух других осей.
).
Аналогично и для двух других осей.Прямоугольные все системы координат в трехмерном пространстве делятся на два класса - правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений. (На рис.2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами[3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта итп (положительное направление осей выбирают так, чтобы при повороте оси
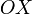 против
часовой стрелки на 90° её положительное
направление совпало с положительным
направлением оси
против
часовой стрелки на 90° её положительное
направление совпало с положительным
направлением оси ,
если этот поворот наблюдать со стороны
положительного направления оси
,
если этот поворот наблюдать со стороны
положительного направления оси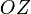 ).
).Направленные отрезки.Упорядоченная пара точек (А,В) называется напрвленным отрезком с началом в точке А и концом в точке В. Обозначается:
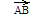
Направленный отрезок
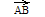 изображается
стрелкой, идущей из его начала в его
конец (рис.1).Направленный отрезок
изображается
стрелкой, идущей из его начала в его
конец (рис.1).Направленный отрезок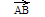 называют
такжесвязанным
вектором,
а точку А - точкой
его приложения.Если
точки А и В различны, то напрвленный
отрезок
называют
такжесвязанным
вектором,
а точку А - точкой
его приложения.Если
точки А и В различны, то напрвленный
отрезок
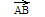 называетсяненулевым;
если же точки А и В совпадают, то
направленный отрезок
называетсяненулевым;
если же точки А и В совпадают, то
направленный отрезок
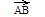 ,
точнее,
,
точнее,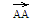 называетсянулевым
и обозначается символом θA.
называетсянулевым
и обозначается символом θA.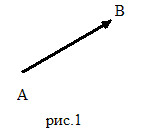
Напрвленный отрезок
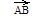 называетсяпараллельным
прямой l (плоскости Р),
если либо он нулевой , либо прямая АВ
параллельна прямой l (соответственно
плоскости Р).
называетсяпараллельным
прямой l (плоскости Р),
если либо он нулевой , либо прямая АВ
параллельна прямой l (соответственно
плоскости Р).Обозначение:
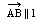 ,
,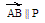 .
.Длиной напрвленного отрезка
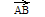 называется
длина отрезка [АВ].
называется
длина отрезка [АВ].Обозначение:
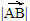 .
Как следует из определения, длина
нулевого и только нулевого направленного
отрезка равнв нулю.
.
Как следует из определения, длина
нулевого и только нулевого направленного
отрезка равнв нулю.Ненулевые напрвленные отрезки
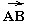 и
и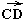 называютсяодинаково
направленными (сонапрвленными),
если лучи [АВ) и [СD) имеют одинаковые
напрвления, и противоположно
напрвленными,
если лучи [АВ) и [СD) имеют противоположные
напрвления.
называютсяодинаково
направленными (сонапрвленными),
если лучи [АВ) и [СD) имеют одинаковые
напрвления, и противоположно
напрвленными,
если лучи [АВ) и [СD) имеют противоположные
напрвления.Обозначение:
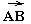 ↑↑
↑↑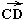 и
и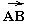 ↑↓
↑↓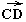 соответсвенно.
соответсвенно.Направленнные отрезки
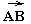 и
и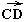 называютсяравными,
если середины отрезков [АD] и [ВС] совпадают
(рис.2)
называютсяравными,
если середины отрезков [АD] и [ВС] совпадают
(рис.2)Обозначение:
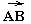 =
=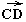 .
Как следует из определения, нулевой
напрвленный отрезок равен любому
другому нулевому и только нулевому
напрвленному отрезку.
.
Как следует из определения, нулевой
напрвленный отрезок равен любому
другому нулевому и только нулевому
напрвленному отрезку.Из свойств параллелограмма (рис.2) следует, что ненулевые направленные отрезки
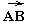 и
и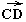 ,
не лежащие на одной прямой, равны тогда
и только тогда, когда четырехугольник
АВDС - параллелограмм. Для равных
ненулевых отрезков, лежащих на одной
прямой, возможен один из четырех
вариантов расположения, изображенных
на рис.2.
,
не лежащие на одной прямой, равны тогда
и только тогда, когда четырехугольник
АВDС - параллелограмм. Для равных
ненулевых отрезков, лежащих на одной
прямой, возможен один из четырех
вариантов расположения, изображенных
на рис.2.
