40 Схема Бернулли. Формула Пуасова. Локальная и интегральные формулы Моавра-Лапласа

Проводятся опытов, в каждом из которых может произойти определенное событие («успех») с вероятностью p (или не произойти — «неудача» —). Задача — найти вероятность получитьуспехов в опыте.

Решение:

Количество успехов — величина случайная, которая имеет распределение Бернулли.

Определение

Теперь рассмотрим эту задачу подробнее. Возьмём самый простой стохастический эксперимент с двухэлементным пространством элементарных событий. Одно назовём «успехом», обозначим «1», другое — «неудачей», обозначим «0».

Пусть вероятность успеха , тогда вероятность неудачи.

Рассмотрим новый стохастический эксперимент, который состоит в -кратном повторении этого простейшего стохастического эксперимента.

Понятно, что пространство элементарных событий , которое отвечает этому новому стохастическому эксперименту будет(1),. За-алгебру событийвозьмёмбулеан пространства элементарных событий (2). Каждому элементарному событиюпоставим в соответствие число. Если в элементарном событииуспех наблюдаетсяраз, а неудача —раз, то. Пусть, тогда. Также является очевидной нормированность вероятности:.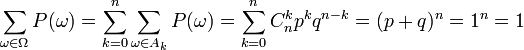

Поставив в соответствие каждому событию числовое значение(3), мы найдём вероятность. Построенное пространство, где Ω — пространство элементарных событий, определено равенством (1),—-алгебра, определена равенством (2), P —вероятность, определена равенством (3), называется схемой Бернулли для испытаний.

Набор чисел называется биномиальным распределением.

Расширенное определение

Обычная формула Бернули применима на случай когда при каждом испытании возможно одно из двух cобытий. Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из событий с вероятностью, где. Вероятность появленияраз первого события и- второго ираз k-го находится по формуле

,

где

Свойства

Пусть p - вероятность успеха в схеме Бернулли, q=1-p. Тогда самым вероятным среди событий является событие, гдеможно найти с неравенства.

Формула Бернуллиудобна для вычислений лишь при сравнительно небольшом числе испытаний. При больших значенияхпользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.

Теорема. Если вероятность наступления событияв каждом испытании постоянна и мала, а число независимых испытанийдостаточно велико, то вероятность наступления событияровнораз приближенно равна

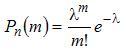,(3.4)

где .

Доказательство. Пусть даны вероятность наступления события в одном испытаниии число независимых испытаний. Обозначим. Откуда. Подставим это выражение в формулу Бернулли:

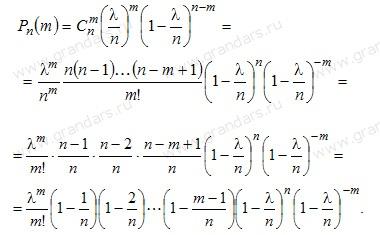
При достаточно большом !!n,, и сравнительно небольшом !!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.

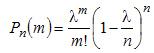
Учитывая то, что достаточно велико, правую часть этого выражения можно рассмотреть при, т.е. найти предел

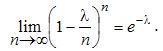
Тогда получим

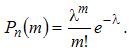(3.5)

Пример. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.

Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5).

Находим .

Воспользуемся формулой Пуассона

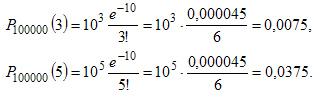
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

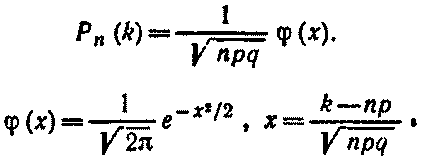
Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

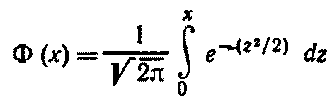
-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

Пример. Найти вероятность того, что событие А насту пит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение. По условию, n=243; k = 70; р =0,25; q= 0,75. Так как n=243 - достаточно большое число, воспользуемся локальной теоремой Лапласа:

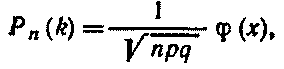
где х = (k—np)/ √npq.

Найдем значение х

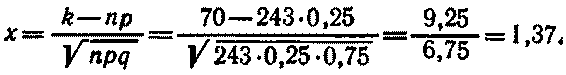
По таблице п найдем ф(1,37) =0,1561. Искомая вероятность

P(243)(70) = 1/6,75*0,1561 =0,0231.