29 Таблица основных неопределённых интегралов.

Таблица основных неопределенных интегралов

33 Нахождение площадей плоских криволинейных фигур.Длина дуги.Объём тела вращения.

18.1.1. Площадь плоской фигуры в декартовых координатах

 а) Допустим, что фигурапредполагает наличие границы

является криволинейной трапецией и, при условии, чтона

Еслинаходится ниже оси(рис. 18.1), то

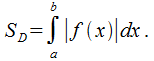
Рис. 18.1

Пример:

 

 

(рис. 18.1, б).

 

 

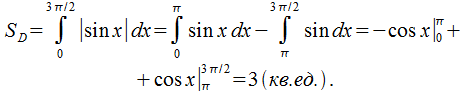
б) Предположим, что для фигурыхаракерно наличие границыПлощадь(рис. 18.2, а),

Рис. 18.2

 соответственно получаем формулу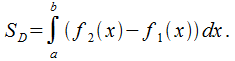

В общем случае площадь находится с помощью формулы

 

 

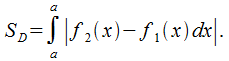
Пример:

(рис. 18.2, б).

 

 

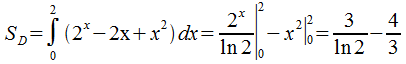
18.1.2. Площадь криволинейной трапеции при параметрическом задании кривой

 Предположим, что для криволинейной трапециихарактерно наличие границы

 

.

 

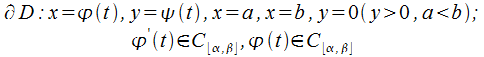Используя метод подстановки, запишем формулу

 

 

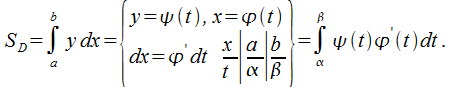
Пример:

 

  Рис. 18.3

 

18.1.3. Площадь криволинейного сектора в полярных координатах

 

О: Под полярной системой координат понимается совокупность т.(полюса) и исходящей из данной точки направленной полупрямой(полярной оси). В качестве полярных координат т.обозначают числа(полярный радис) и(полярный угол) (рис. 18.4, а).

  Рис. 18.4

 Примежду точками плоскости и парами чиселформируется взаимно однозначное соответствие.

Допустим, что начало прямоугольной системы координатсовпадает с полярной осью. В этом случае зависимость между кординатами т.в декартовой и полярной системах находится с помощью формул (рис. 18.4, б).

 

(18.1)

 

 

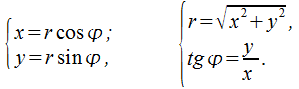
Для определения, поскольку формулы (18.1) дают два значения полярного угла отдо.

Линию в полярной системе находят с помощью уравнения. Допустим,является уравнением окружности с центром в полюсе и радиусом(рис. 18.5, а);представляется в качестве уравнения трехлепестковой розы (рис. 18.5, б).

  Рис. 18.5

 О: Под криволинейным сектором в полярной системе координат понимается фигура, имеющая границу(рис. 18.6, а).

Для вычисления площади криволинейного сектора разделим его начастей с помощью лучейПредставим, чтоявляется длиной некоторго радиус-вектора, находящегося в(рис. 18.6, б).

  Рис. 18.6

В качестве площади криволинейного сектора можно представить

 

 

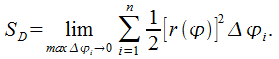
Учитывая то, что в правой части данного уравнения обозначена интегральная сумма для функциина отрезке, в итоге можно записать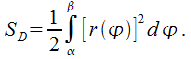

Пример: Определить площадь, которая являтся ограниченной трехлепестковой розой(рис. 18.5, б).

 

Достаточно найти площадь половины одного лепестка при. В этом случае

 

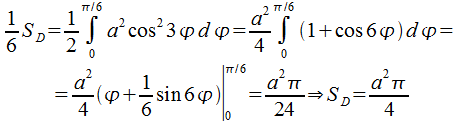
Центральный угол — это угол, образованный двумя радиусами. Длина дуги, описываемой концом радиуса, пропорциональна величине соответствующего центрального угла. Центральный угол дуги измеряется градусами. Для измерения градусами - целая окружность имеет 360°. Половина окружности 180°.

Длина дуги, пропорциональна ее радиусу и величине центрального угла.

1.	p= 2π r n 360 = π r n 180

(r - радиус дуги, n - центральный угол дуги в градусах.)

Пусть криволинейная трапеция D c границей

вращается вокруг оси ОХ. Поперечными сечениями являются круги с радиусами у (х), поэтому

и

Пусть криволинейная трапеция D с границейх = х(у),у=с, y=d(c<d),x = 0 вращается вокруг оси OY, тогда

Пример: Определить объем тела, образованного вращением фигуры D с границей= 4 - х, х = 0: а) вокруг оси ОХ;

б) вокруг оси OY.

При вращении фигуры D вокруг оси ОХ получим параболоид (рис. 18.8, а), объем которого

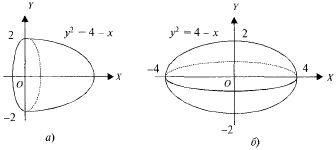
Рис. 18.8

При вращении фигуры D вокруг оси OY получаем тело, изображенное на рис. 18.8, б. Его объем