Глава 5. Термодинамика однокомпонентных систем

5.1. Термодинамические потенциалы идеальных газов

Как уже отмечалось, в идеальном газе отсутствуют силы межмолекулярного взаимодействия, а уравнением состояния является уравнение Менделеева – Клапейрона

pV=nRT, (5.1)

где R– универсальная газовая постоянная, представляющая собой работу расширения газа при повышении температуры на 1 К,n– число молей газа.

Так как внутренняя энергия идеального газа не зависит от объема и давления, а является лишь функцией температуры, то на основании уравнения (2.7) после его интегрирования получим для внутренней энергии при любой температуре T:

U_Т=U_о+с_V(Т–Т_o). (5.2)

Энтальпия идеального газа, как и внутренняя энергия, также зависит только от температуры. Так как, по определению, H=U+pV, а для 1 моля газаpV=RTи (с_р–с_V) =R, то

Н=U_о+с_р(Т–Т_o). (5.3)

Изохорный и изобарный потенциалы идеального газа при постоянной температуре определяются интегрированием уравнений (4.28) и (4.34). Для одного моля идеального газа при T= const

dF= –pdV= –dV, (5.4)

откуда после интегрирования получаем

F=F(Т) –RTlnV. (5.5)

Для изобарного потенциала

dG=Vdp=dp, (5.6)

откуда

G=G(Т) +RT lnp. (5.7)

Величины F(T) иG(T) в уравнениях (5.5) и (5.7) представляют собой константы интегрирования, зависящие от температуры, но их значения неизвестны, а поэтому и величиныFиGостаются неопределенными. Однако на практике обычно важно знать не абсолютные значения термодинамических потенциалов, а их изменения в том или ином процессе, и приведенные уравнения позволяют рассчитывать эти изменения. Например, при изотермическом расширении (сжатии) моля идеального газа изменение изобарного потенциала будет равно

G=G₂–G₁=G(Т) +RTlnp₂–G(Т) –RTlnp₁=RTln(р₂/р₁). (5.8)

Постоянные G(T) сокращаются, так как при заданной температуре они одинаковы при любых давлениях.

5.2. Реальные газы. Летучесть

Уравнения для термодинамических потенциалов реальных газов также можно, в принципе, получить на основании уравнений состояния. Однако в действительности мы не имеем уравнения состояния реального газа, которое описывало бы связь между параметрами состояния при любых условиях. Единственным теоретически обоснованным уравнением для реальных газов является уравнение со вторым вириальным коэффициентом

pV=RT(1 +В/V), (5.9)

где

В=В_о+/Тⁿ– /Т^m. (5.10)

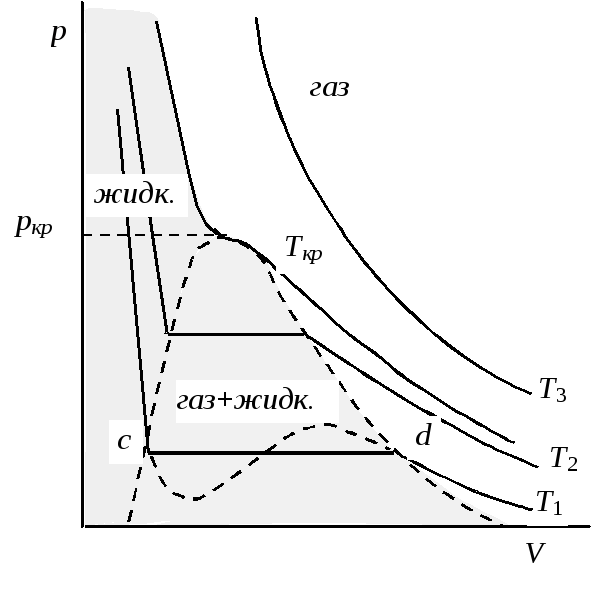
Рис. 5.1. Изотермы реальных газов (Т₁< Т₂ < Т_кр < Т₃)

Это уравнение выведено методами статистической механики и имеет большое теоретическое значение, но не представляет существенного практического интереса вследствие сложности определенияBи правильности уравнения только при малых отклонениях от законов идеального газа.

Широко известно уравнение Ван-дер-Ваальса:

(р+а/V²)(V –b) =RT, (5.11)

которое характеризует не только изменения состояния газа, но и жидкости. Постоянные a и b для каждого газа вычисляются из его критических параметров. Однако количественно это уравнение не всегда отвечает экспериментальным данным, а опытные значения a и b в обычных условиях примерно в два раза меньше рассчитанных. Уравнение также непригодно для высоких давлений.

Наиболее удовлетворительные результаты дает уравнение Битти – Бриджмена:

pV²=RT [V+В_о(1 –b/V)] /(1 –с/VT³) –А_о(1 –а/V), (5.12)

где a,b,c,A,B– эмпирические константы, характерные для каждого газа.

В настоящее время известно более 150 уравнений состояния газов, большинство из которых является эмпирическими, и применимы лишь в определенном интервале температур и давлений. Кроме того, применение таких уравнений приводит к сложным формулам для термодинамических потенциалов, зачастую непригодных для проведения практических расчетов.

Г. Льюис предложил метод расчета термодинамических характеристик реальных газов, основанный на том, что для них формально сохраняются те же соотношения, что и для идеальных газов, но вместо давления вводится новая функция f–термодинамическая летучесть(илифугитивность), более кратко – летучесть.

Для изобарного потенциала постулируется для моля газа

GG(Т) +RTlnf. (5.13)

Дополнительно вводится условие, согласно которому по мере уменьшения давления величина летучести приближается к величине давления:

lim f/р1 прир 0. (5.14)

Из (5.13) следует, что для изотермического процесса

G=G₂–G₁=RTln(f₂/f₁). (5.15)

Значения fнужно найти для каждого реального газа при различных давлениях и температурах. Основой для вычисления летучести являются уравнения (5.13) и (5.14).

Продифференцируем уравнение (5.13) по давлению при T= const:

(G/р)_Т=RT(lnf/р)_Т. (5.16)

Так как (G/р)_Т=V, то из уравнения (5.16) получим:

dlnf=dp. (5.17)

Интегрирование в пределах между состояниями 1 и 2 дает:

. (5.18)

Для аналитического решения этого уравнения необходимо знать зависимость объема реального газа от давления (например, по уравнению Ван-дер-Ваальса), и подставить ее в подинтегральное выражение.

Более точным является метод, основанный на графическом нахождении интеграла. Для этого экспериментально определяют объем, занимаемый молем газа при разных давлениях при заданной температуре и строят график зависимости Vотp. Величину интеграла определяют как площадь под полученной кривой.

Другой способ заключатся в том, что вначале находят объемную поправку, характеризующую степень отклонения объема реального газа от вычисленного по уравнению Менделеева – Клапейрона:

=–V. (5.19)

Тогда уравнение (5.18) можно записать в виде

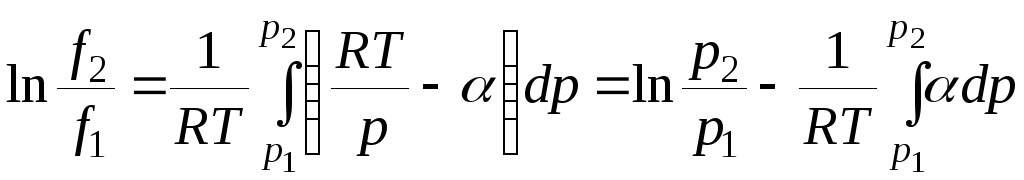. (5.20)

При р₁ 0 летучесть f₁ р₁и, отбрасывая индекс 2, получаем:

lnf= lnp–. (5.21)

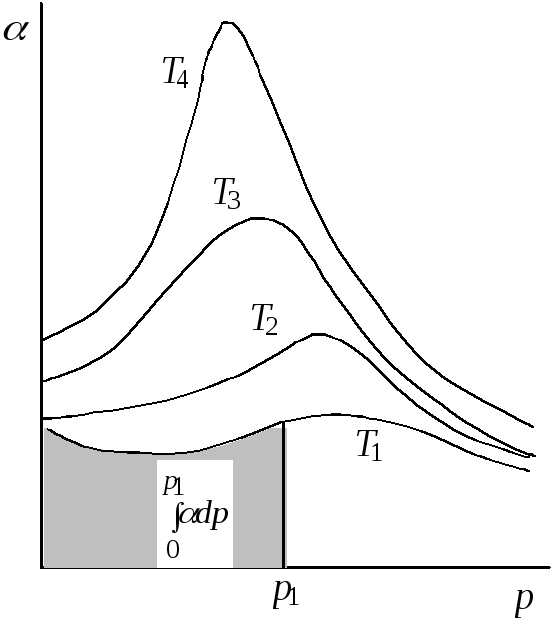Рис.5.2. Зависимость объемной поправки от давления (Т₁< Т₂< Т₃< Т₄)

Для определенияfстроят график зависимости= (р) (рис. 5.1) и графическим интегрированием находят второй член справа уравнения (5.21) при разных величинах давлений.

Летучесть при больших давлениях и низких температурах сильно отличается от давления, например, при T=273 К иp=1200 атмf_СО= 2663, а для азота приT = 198 К иp=6000 атмf= 2•10⁶.

Летучесть можно определить как давление, которое должен производить идеальный газ, чтобы оказывать такое же действие, как и реальный газ. С приближением реального газа к идеальному состоянию fпо величине приближается кp, и для идеального газа обе величины становятся одинаковыми. Отношениеf/pназываюткоэффициентом летучестииликоэффициентом активности:

=f/р. (5.22)

При малых величинах и малых давлениях можно считатьпостоянной, тогда

lnf= lnp–. (5.23)

и

. (5.24)

Показательную функцию можно разложить в ряд, ограничившись двумя членами разложения, в результате чего получим:

иf = , (5.25)

где p_ид– давление, которое имел бы идеальный газ, если бы он занимал тот же объемV, что и реальный газ при заданной температуре.

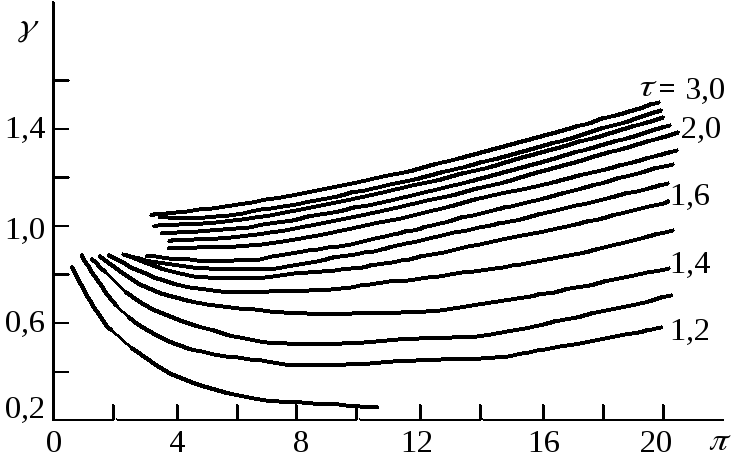
Описанные методы расчета летучести требуют экспериментального определения объема газа при разных давлениях и температурах. Во многих случаях такие данные отсутствуют, и тогда можно воспользоваться обобщенным методом расчета, основанным на принципе соответственных состояний. Если выражать свойства газов не черезp,V,T, а с помощью безразмерных единиц –приведенных параметров– приведенного давления=р/р_кр, приведенного объема=V/V_кр, и приведенной температуры=Т/Т_кр, то можно получить приведенное уравнение состояния (,,) =0, в которое не входит ни одна из величин, характеризующих данное вещество. Согласно принципу соответственных состояний,при одинаковых приведенных параметрах различные реальные газы имеют ряд одинаковых свойств, в том числе и коэффициенты летучести.

Рис. 5.3. Схематическое изображение зависимости коэффициентов летучести от приведенного давления при разных приведенных температурах

Таким образом, достаточно получить данные о коэффициентах летучести одного газа при различных приведенных давлениях и температурах и эти данные можно использовать для расчетов летучести других газов. Однако, следует отметить, что принцип соответственных состояний является приближенным и строго не выполняется.