4.4. Адіабатний (ізоентропійний) процес

Адіабатний процес – такий термодинамічний процес, що відбувається у фізичній системі, яка не отримує та не віддає теплоту, тобто в даній системі відсутній теплообмін між робочим тілом та навколишнім середовищем. Отже

dq = 0, q = const

та

ds = const, s = const.

Приклад: процеси стискання газу (робочого тіла), які відбуваються настільки швидко, що теплота не встигає передатися від нього до навколишнього середовища та навпаки.

1. Графічне зображення процесу:

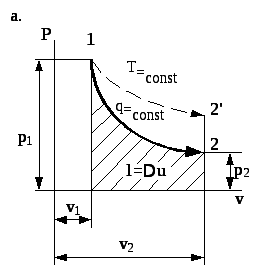
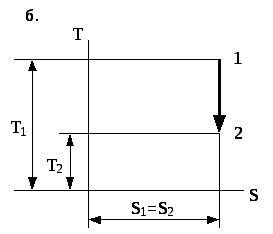
Рис. 4.6. Зображення адіабатичного процесу в координатах p- та T-s

2. Зв’язок між параметрами газу - рівняння стану адіабатичного процесу.

Запишемо рівняння 1-го закону термодинаміки

в 1-ій формі:

dq = du + pd,

де

du = C_ dT,

та в 2-ій формі :

dq = di - dp,

де

di = C_p dT.

Але в адіабатичному процесі dq_ад = 0. Тоді ці рівняння можна записати у вигляді:

C_ dT = -pd (a)

та

C_p•dT = •dp (б).

Знайдемо відношення цих величин поділивши рівняння (б) на (а):

C_p•dT/ C_ dT = - •dp/ pd,

тобто

C_p/C_ = •dp/ pd.

Звідки

k = C_p/C_,, (4.38)

або

k = - •dp/ pd, (4.39)

де k - показник адіабати.

Отже

k•p•d = •dp. (4.40)

Шляхом інтегрування останнього рівняння отримаємо рівняння Пуассона:

p•^k = const. (4.41)

Отже, в координатах p- адіабата зображається нерівнобокою гіперболою p•^k = const, а так як k  1, то адіабата 1-2 буде розміщена крутіше ізотерми 1-2 (рис. 4.6а). Звідси випливає, що при однаковому ступені розширення

_ад  _т.

Таким чином, рівняння, які описують зв'язок між параметрами стану ідеального газу в адіабатному процесі, будуть мати наступний вигляд:

_2/₁ = (p₁/p₂)^1/k;

p₁/p₂ = (_2/₁)^k;

T₁/T₂ = (_2/₁)^k-1;

T₁/T₂ = (p_1/p₂)^(k-1)/k, (4.42)

де k - показник адіабати (ізоентропи).

3. Робота розширення системи.

Із рівняння

dq = du + pd

очевидно, що для будь-якого адіабатного процесу (dq = 0) справедливо

du_ад = -p•d. (4.43)

Отже, відсутність теплообміну при протіканні адіабатного процесу вказує на те, що робота розширення ідеального газу здійснюється за рахунок зменшення внутрішньої енергії газу:

l_ад = -(u_ - u_ = u₁ - u₂. (4.44)

Але відомо, що

du = C_•d,

тоді

l_ад = C_•(_ - _). (4.45)

Отже, адіабатне розширення ідеального газу викликає зниження його температури, а стиснення - підвищення.

Але p• = R_i T, тоді

l_ад = C_•(p₁•₁ – p₂•₂)/R_i. (4.46)

Але R_i = C_•(k-1), тоді

l_ад = (p₁•₁ – p₂•₂)/(k-1) = R_i T•[1 - (p_1/p₂)^(k-1)/k]/(k-1) =

= p₁•₁•[1-((p_1/p₂)^(k-1)/k)]/(k-1). (4.47)

На p- -діаграмі (рис. 4.6а) робота розширення робочого тіла буде еквівалентна площі під кривою процесу 1-2.

4. Кількість теплоти, підведеної до системи (робочого тіла) в адіабатному процесі.

Із визначення оборотного адіабатного процесу: кількість теплоти, яка підводиться в ізотермічному процесі до робочого тіла або відводиться від нього, дорівнює нулю.

dq_ад = 0, та q_ад = const. (4.48)

5. Теплоємність газу в адіабатному процесі

Із визначення теплоємності: C = dq/dT , але для адіабатного процесу

dq_ад = 0,

тоді

C_ад = 0 = const. (4.49)

Цей висновок очевидний: якщо в системі здійснюється адіабатний процес, то температура в системі змінюється, хоча теплота до системи і не підводиться (тобто, ця зміна відбувається тільки за рахунок зміни внутрішньої енергії робочого тіла).

6. Зміна ентропії газу в адіабатному процесі.

Із визначення ентропії: ds= dq/T, але оскільки в адіабатному процесі

ds_ад. = q/, а q_ад. = 0, то для нього справедливий наступний запис:

ds_ад = 0, або S = const, (4.50)

тобто, оборотний адіабатний процес є процесом ізоентропійним. Отже, в координатах -s (рис. 4.6б) адіабатний процес зобразиться у вигляді прямої, яка паралельна до осі ординат.

7. Зміна внутрішньої енергії та ентальпії робочого тіла (газу) в адіабатному процесі.

Зміна внутрішньої енергії робочого тіла (газу) та виконана ним робота рівні за величиною, але протилежні за знаком. Тобто,

u_ад = - l_ад; (4.51)

а також

du = C_ dT,

тобто

u_ад = C_ (T₂ - T₁). (4.52)

Зміна ентальпії газу в адіабатному процесі:

di = C_p•dT,

тобто

i_ад = C_p•(T₂-T₁). (4.53)

8. Частка теплоти, яка затрачається на зміну внутрішньої енергії газу в адіабатному процесі.

_ад = u_ад/q_ад = - l_ад/q_ад. (4.54)

Отже, в адіабатному процесі внутрішня енергія системи змінюється не за рахунок підведеної теплоти (яка не підводиться і не відводиться, тобто q_ад = 0), а тільки за рахунок виконаної робочим тілом роботи.