4.3. Ізотермічний процес

Ізотермічний процес - процес, який відбувається у фізичній системі при постійній температурі (T = const, dT = 0).

Приклад: перехід робочого тіла (газу) із рідкого (скрапленого) стану у пароподібний і навпаки - скраплення газоподібного робочого тіла (конденсація). Ці процеси відбуваються при постійній температурі.

1. Графічне зображення ізотермічного процесу

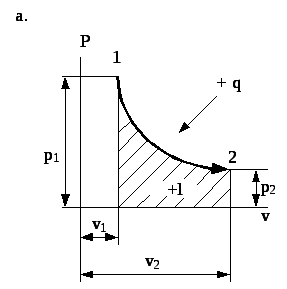
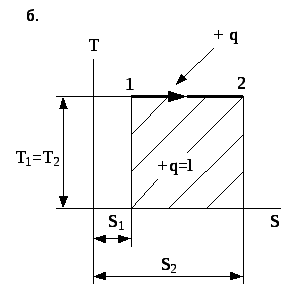
Рис. 4.5. Зображення ізотермічного процесу в P- та T-s координатах.

2. Зв’язок між параметрами.

Рівняння Клапейрона p•/T = const при T = const приймає вигляд

p• = const тa p• = R_i T = const.

Рівняння стану ізотермічного процесу (за рівнянням Бойля- Маріотта) можна записати у вигляді:

p_l•_l = p_•_ або p_l/p_ = _/_{l .} (4.26)

Залежність об’єму від тиску на ізотермі в p- - координатах для ідеального газу має характер рівнобокої гіперболи (рис. 4.5а). Тобто, в ізотермічному процесі при підвищенні тиску газу його об’єм зменшується.

3. Робота розширення системи від стану 1 до стану 2 визначається із загального рівняння:

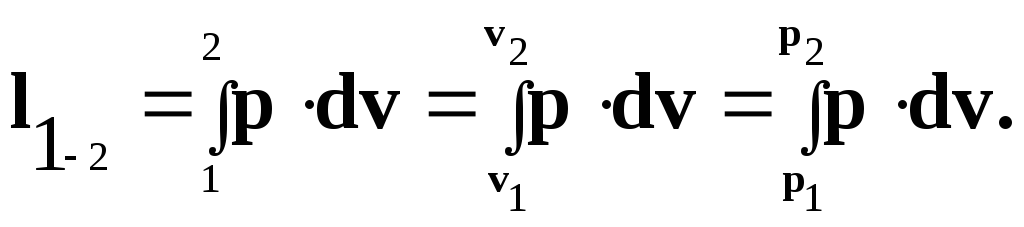(4.27)

Для ідеального газу дане рівняння можна представити у такому вигляді:

(4.27 a)

Для ізотермічного процесу ці рівняння можна записати наступним чином:

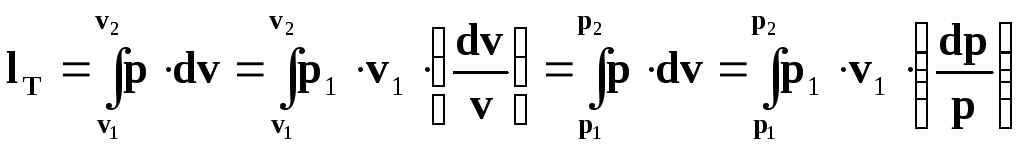(4.28)

Звідки

(4.29)

l_т = R_i•T•ln(_/_l) = R_i•T•ln(р_/р_l). (4.30)

На графіку в p- - координатах робота розширення газу (робочого тіла) зображається площею під кривою 1-2 (рис. 4.5а).

4. Теплота в ізотермічному процесі.

Кількість теплоти, яка підводиться до системи (або відводиться від неї) знайдемо, виходячи із загального рівняння ІІ-го закону термодинаміки:

dq = T•ds,

але так як T = const, то

q_т = T(s₂ - s₁). (4.31)

Запишемо рівняння 1-го закону термодинаміки в І-ій формі:

dq = du + dl,

але в нашому випадку T = const, то

du = C_•dT = 0,

але dT = 0, тоді

dq_т = C_•dT + dl_т = dl_т, або dq_т =dl_т, (4.32)

де роботу необхідно визначити за рівнянням (4.30).

В умовах ізотермічного процесу вся підведена до робочого тіла теплота витрачається на виконання ним роботи. На T-s -діаграмі кількість теплоти визначається площею під лінією 1-2-(прямокутник із основою s та висотою T).

5. Теплоємність в ізотермічному процесі.

Відомо, що

C = dq/dT,

але в ізотермічному процесі

dT = 0,

тоді

С_т = ± ∞. (4.33)

Тобто, для ізотермічного процесу, для якого підведення або відведення теплоти не призводить до зміни температури системи, теплоємність ідеального газу нескінченно велика. Знак «плюс» відповідає підведенню теплоти до системи, знак «мінус» – відведенню теплоти від системи.

6. Зміна ентропії в ізотермічному процесі.

Зміну ентропії в ізотермічному процесі 1-2 визначимо за рівнянням:

ds = dq/T, але dq_т =dl_т,

то можна записати, враховуючи рівняння (4.30):

ds_т = dl_т/T,

s_ = l_/=q_/.

Або, враховуючи рівняння (4.30), отримаємо:

s₂ - s₁ = R_i ln(₂/₁)= R_i•ln(p₁/p₂). (4.34)

7. Зміна внутрішньої енергії та ентальпії робочого тіла в ізотермічному процесі.

Із визначення: внутрішня енергія ідеального газу не залежить від об’єму, а залежить тільки від температури. Тобто

dU = C_ d, або U = C_•_ - _.

Але в ізотермічному процесі dT = 0, тобто

T = const,

тому

U₂ = U₁.

Отже

ΔU = 0. (4.35)

А також

i = C_p•_ - _ = 0,

тобто

i = i_ - i_ або i_ = i_.

Отже

i = 0. (4.36)

Таким чином, в ізотермічному процесі внутрішня енергія та ентальпія ідеального газу залишаються постійними.

8. Частка теплоти, яка затрачається на зміну внутрішньої енергії газу (робочого тіла).

Відомо, що α = Δu/q, але для ізотермічного процесу  = const звідки

Δu = 0,

тому

α_т = 0. (4.37)

Тобто, в ізотермічному процесі підведена до робочого тіла теплота витрачається тільки на виконання ним роботи , так як зміни його внутрішньої енергії не буде.