За рівнянням першого закону термодинаміки

dq = du + dl = du + pd, але dl = 0,

тоді

dq_v = du та q_v = u. (4.9)

Отже

du_v = C_vdT,

або

Δu = q_v = C_v (T₂-T₁). (4.10)

8. Частка теплоти, яка затрачається в ізохорному процесі на зміну внутрішньої енергії робочого тіла:

.

Для ізохорного процесу вираз, що описує алгоритм розподілення теплоти, яка підводиться до робочого тіла, має вигляд:

Вся теплота, яка підводиться до системи ідеального газу в ізохорному процесі, затрачається на зміну його внутрішньої енергії.

Практичне застосування - розрахунок необхідної товщини стінки газгольдера при збільшенні тиску в системі в результаті підведення теплоти до газу, який знаходиться в ньому .

4.2. Ізобарний процес

Ізобарний процес - процес, який відбувається у фізичній системі при постійному тиску (р = const, dр = 0).

Приклад: процеси, які проходять в спеціальній споруді для зберігання газу в ізобаричних умовах (в ізобаричному газгольдері).

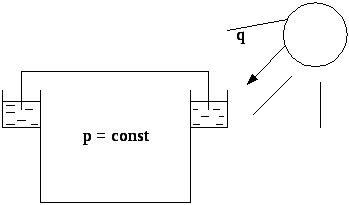
При нагріванні Сонцем газ розширюється, його об’єм збільшується і кришка апарата піднімається підтримуючи тиск в апараті постійним.

Рис. 4.3. Схема ізобарного газгольдера

1. Графічне зображення ізобарного процесу.

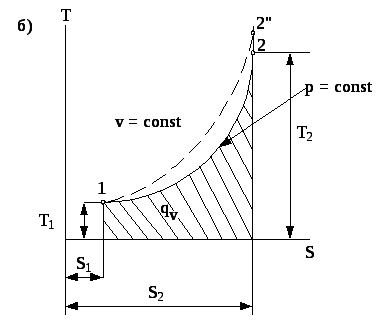
Рис. 4.4. Зображення процесу в координатах p- v (а) та T-s (б).

2. Зв’язок між параметрами.

Рівняння стану ідеального газу p/T = const для ізобарного процесу приймає вигляд:

. (4.11)

А також

або . (4.12)

Тобто, при зростанні температури газу пропорційно зростає і його об’єм.

3. Робота ізобарного процесу.

Робота розширення системи в ізобарному процесі 1-2 при p = const розраховують за рівнянням:

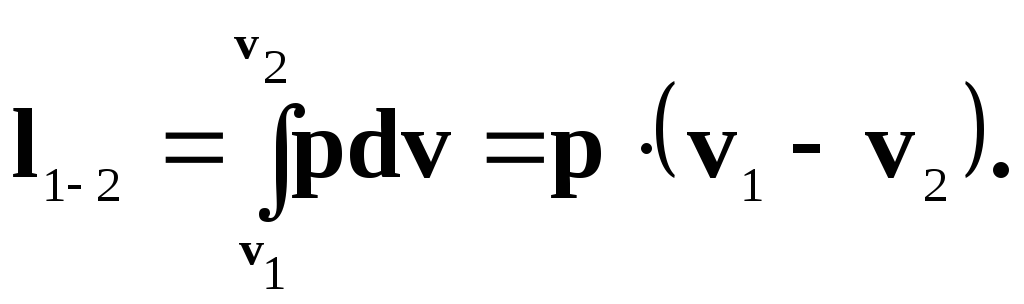
Для ізобарного процесу (р = const) робота розширення газу буде дорівнювати:

(4.13)

Але так як p_v = R_іT, то

(4.14)

На p- - діаграмі площа заштрихованого прямокутника (рис. 4.4а) буде еквівалентна роботі ізобарного процесу (роботи розширення газу)

3. Теплота ізобарного процесу.

Кількість теплоти, яка підводиться до системи при нагріванні газу в ізобарному процесі визначимо із наступних міркувань.

Із рівняння 1-го закону термодинаміки (2-гої форми запису)

dq = di - dp

випливає, що для ізобарного процесу (dp = 0)

dq_p = di, або q_p = Δi. (4.15)

Значить, кількість теплоти, підведеної до робочого тіла (газу) в ізобарному процесі, дорівнює різниці ентальпій.

Кількість теплоти можна підрахувати також із наступних рівнянь:

, або ,

звідки

, або q_p = C_p∙∙T. (4.16)

На T-s - діаграмі (рис. 4.4б) цей процес зображається кривою 1-2, а заштрихована площа, яка знаходиться під цією кривою еквівалентна кількості теплоти, якапідводиться до системи в ізобарному процесі.

5. Зміна ентропії ідеального газу в ізобарному процесі (при C_p = const) описується наступним рівнянням:

ds_p = dq_p/T = C_p•dT/T. (4.17)

Проінтегруємо дане рівняння та отримаємо:

s_p = C_p•ln(T_/T_) = C_p •ln(_/_)_. (4.18)

Звідси випливає, що в координатах T-s процес зображається логарифмічною кривою 1-2 (рис. 4.4б).

Розраховуємо зміну ентропії, використовуючи рівняння 1-го закону термодинаміки (1-шу форму запису):

dq = du + pd

та рівняння Клапейрона:

p• = R_i T або p/T = R_і/.

Тоді

ds_p = dq_p/T = (du + pd)/T = du/T + pd/T.

Нами вже доказано (рівняння 4.6), що du = C_•dT, а також відомо, що p/T = R_i/, тоді попереднє рівняння запишемо у вигляді:

ds_p = C dT/T + R_i d/, (4.19)

або, логарифмуючи це рівняння, отримаємо:

s_ – s₁ = C_ ln(T_/T₁) + R_i•ln(_/₁)=C_•ln(T_/T_l) + R_i•ln(T_/T_l) =

= C_•ln(_/_l) + R_i•ln(_/_l)=C_•ln(_/_l) + R_i•ln(T_/T_l). (4.20)

Отже, теплота в ізобарному процесі тратиться на зміну внутрішньої енергії та виконання роботи. Тобто

ΔS = ΔU + L або s = u + l.

6. Теплоємність газу в ізобарному процесі.

В загальному вигляді C = dq/dT. Але в ізобарному процесі dq_p = di.

В нашому випадку, при р = const отримаємо:

C_p = dq_p/dT_p або C_p = q_p/(Т₂ - Т₁). (4.21)

Але, так як dq_p = di, то отримаємо:

C_p = di/dT або C_p = i/(Т₂ - Т₁). (4.22)

Якщо порівняти формули (4.18) та (4.8), то можна побачити, що так як C_p > C_ , то в одному і тому ж інтервалі температур T_l та T₂ зміна ентропії в ізобарному процесі буде більшою ніж в ізохорному, тобто крива процесу р = const пройде нижче, ніж крива процесу v = const.

7. Зміну внутрішньої енергії робочого тіла (газу) в ізобарному процесі можна підрахувати за формулою (4.9):

du_p = C_•dT або u_p = C_•(T_ - T_l). (4.23)

Тобто

Δu = C_•ΔT.

8. Частка теплоти, яка затрачається на зміну внутрішньої енергії газу:

= Δu/q_p. (4.24)

Але для ізобарного процесу

Δu = C_•ΔT та q_p = C_p•ΔT.

Тоді

= C_/C_p = l/k, (4.25)

де k - коефіцієнт адіабати. Так як C_p > C_, то k > l. Наприклад, для повітря k = 1,4, тоді _пов = 0,715. Тобто, в ізобарному процесі із всієї підведеної до робочого тіла теплоти 71% її кількості витрачається на зміну його внутрішньої енергії і тільки 29% - на виконання ним роботи.

Практичне застосування - підрахунок необхідного об’єму газгольдера при максимально можливій кількості підведеного від Сонця теплоти (щоб не скинуло кришку із резервуара)