1.4. Повнота системи елементарних дій над критеріями (методів згортання)

Використовуючи різні комбінації описаних у попередньому параграфі методів згортання критеріїв, можна відобразити всю широту можливих однозначних залежностей критерію об’єднаної операції від критеріїв частинних операцій. Це випливає з низки результатів, наведених у книзі Гермейєра.

Теорема 1. Якщо однозначна функція і кожний з критеріївнабувають лише скінченну кількість скінченних можливих значень, то залежністьвідможе бути подана за допомогою скінченої кількості дій типуIV ( тобто (1.27)−(1.29) ), I і II ( формули (1.22) і (1.25) відповідно).

Д о в е д е н н я. Нехай − можливі дискретні значення-го критерію,, занумеровані у порядку зростання.також, очевидно, набуває значення із скінченної множини,.

Розглянемо функції

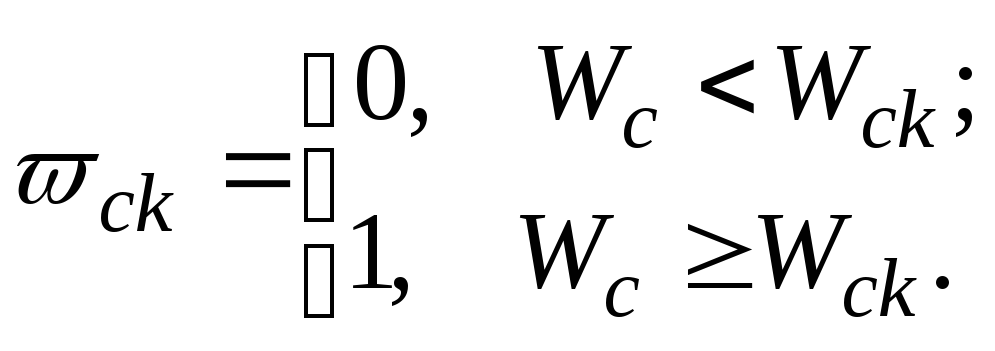
Оскільки є функцією від, то вона є і функцією від. Очевидно, що

, (1.35)

де . Отже,утворена зспособом І (1.22).

Нехай аналогічно визначаються за правилом

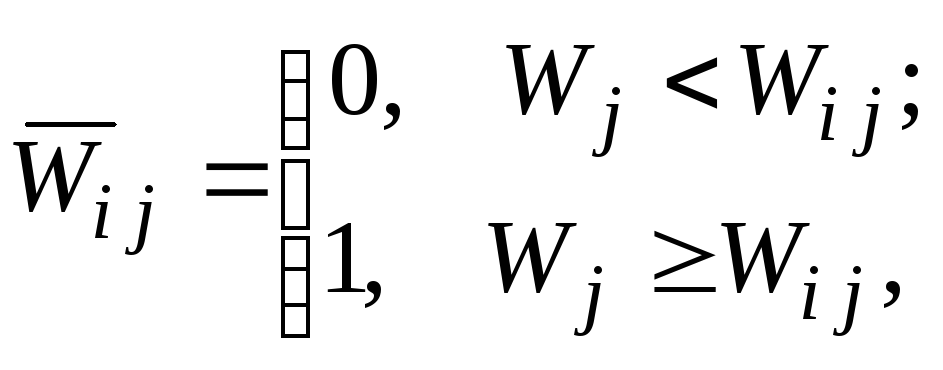
. (1.36)

Таким чином, функції утворені з, використовуючи спосіб ІІ. Крім того,

(1.37)

Тому , які є функціями від, можуть бути записані як функції від. Оскількиіє бульовими змінними, які набувають значень з множини, то за відомою теоремою математичної логіки, залежністьвідможе бути подана¹ як послідовність дій типу IV.

Але оскільки самі виражаються черезза способом ІІ, а− черезза формулою (1.35), тобто за допомогою правила І, то теорему доведено. Дана теорема вичерпує всі результати щодо точного зображення залежностейу вигляді скінченної кількості елементарних дій.

Наступні теореми встановлюють лише можливість того чи іншого наближеного зображення, але з довільною заданою точністю.

Теорема 2. Нехай набуває скінченну кількість (N) значень , анехай довільні, але обмежені. Тоді, яким би не було, існує множина векторів і функція, утворена за допомогою скінченої кількості дій типу І, ІІ іIV, такі, що

1) , коли ;

2) пробігає всіN значень , якщопробігає значення з , не набуваючи інших значень і при довільних ;

3) утворює -сітку на обмеженій множині всіх, тобто для будь-якоїзнайдеться, віддалена відне більше, ніж на.

Теорема 3. Якщо рівномірна неперервна на деякому паралелепіпеді можливих значень, то вона з довільним ступенем точності може бути зображена у вигляді скінченої кількості дій типу І, ІІ іIV.

Оскільки дії типу V узагальнюють дії типу IV, то система дій І, ІІ і V теж є повною.

Теорема 4. Якщо неперервна на області, то для будь-якогознайдеться така скінченна кількість коефіцієнтівщо у цій області

.

Доведення теорем 2, 4 наведено у Гермейєра.

Зауваження до теореми 4.

A.У формулюванні теореми можна, звичайно, з відповідними змінами коефіцієнтів лінійних форм, брати не мінімакс, а максимін. Для цього достатньо скористатись теоремою 4 для і рівністю

.

В. У сучасній математиці, зокрема, у лінійному і нелінійному програмуванні і теорії ігор, велике значення мають опуклі (вгнуті) функції , які задовольняють нерівність

для будь-яких . Для вгнутих функцій справджується протилежна нерівність. Можна переконатись, що функціїопуклі. Дійсно,

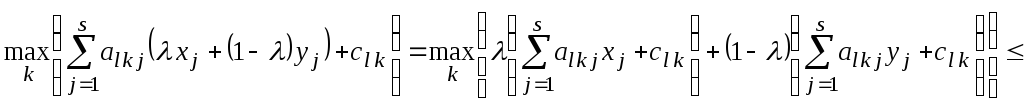
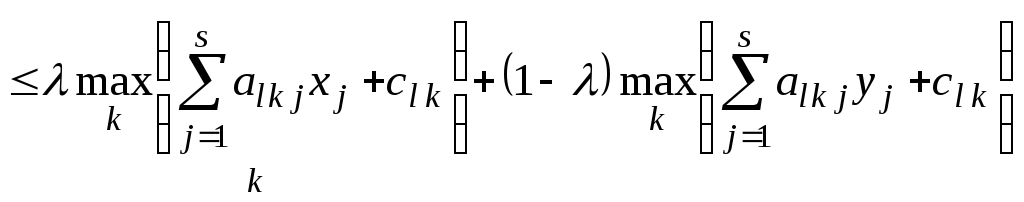¹

Звідси випливає, що будь-яка неперервна в обмеженій області функція з будь-яким наперед заданим ступенем точності наближено дорівнює , де всі − опуклі функції, тобто наближено дорівнює мінімуму, взятому за скінченною множиною опуклих функцій. Зрозуміло, згладжуючи кусково-лінійні опуклі функції, можна завжди вважати досить гладкими, якщо це буде потрібно.

С. Теорема 4 може бути використана і для наближеного подання залежності критерію ефективності від контрольованих і неконтрольованих факторів. Отже, будь-який неперервний критерій ефективності можна подати як мінімакс на множині лінійних функцій або як мінімум на множині опуклих функцій.

D.Як сказано в умовах теореми, , тобто не залежить від точності і області зображення. Навпаки,сильно залежить від точності зображенняі області, у якій ця точність досягається.

Якщо функція задовольняє умови Ліпшиця за всіма аргументами, то . Ця нерівність разом з нерівністюдосить точно описує можливий ступінь складності наближеного запису критерію за допомогою дій додавання і знаходження максимуму і мінімуму.

Отже, теореми 1−4, показують повноту розглянутих елементарних способів об’єднання критеріїв, якщо .Якщо ж де − неконтрольований параметр, то використовуючи при фіксованомунаведені теореми і додаючи спосібVI, одержимо підтвердження повноти способів об'єднання критеріїв і за наявності неконтрольованих факторів.