Модуль 3. Основы дифференциального исчисления.

Теоретические занятия (лекции) – 6 часов.

Лекция 6. (Информационная лекция с использованием средств мультимедиа).

Множества. Функции одной переменной. Предел функции.

Понятие множества. Операции над множествами. Числовые множества. Свойства числовых множеств. Числовая ось, числовые промежутки. Выпуклые множества и их свойства. Функциональная зависимость. Способы ее задания. Основные свойства функции: четность, нечетность, периодичность, монотонность, ограниченность. Основные элементарные функции, их свойства и графики (обзор). Применение функций в экономике (функции спроса и предложения, паутинная модель рынка, функция полезности, кривые безразличия).

Определение предела функции в точке. Теоремы о пределах функций. Два замечательных предела.

Основные понятия теории множеств.

Теория множеств - это наука о множествах самой произвольной природы. Теория множеств служит фундаментом для всех важнейших математических дисциплин. В свою очередь, для теории множеств строится аксиоматическая база. В ней нет определения того, что такое “элемент”, “множество”, “элемент входит в множество” и в виде ряда предложений (аксиом) перечисляются все условия, которые накладываются на эти понятия. Тем не менее, хотя абстрактное математическое понятие множества неопределимо, нетрудно определить какое-либо конкретное множество. Определить конкретное множество – значит уметь ответить на вопрос: принадлежит ли конкретный объект данному множеству или не принадлежит?

Множество - это совокупность объектов произвольной природы. Элемент множества – это объект, принадлежащий данному множеству.

Символическое обозначение (конечного) множества: , где- элементы множества.

Множество может содержать любое число элементов: один, больше одного, ни одного. Множество, состоящее из одного элемента, называется единичным. Множество, не содержащее ни одного объекта, называют пустым и обозначают: В=.

Число элементов множества может быть как конечным, так и бесконечным. В зависимости от их числа множества делятся на конечные и бесконечные. Конечные множества могут состоять из одного или нескольких элементов или вообще не содержать элементов.

Основным понятием теории множеств является понятие принадлежности элемента множеству. Например, говорят: число 3 принадлежит множеству всех натуральных чисел и записывают:, где - символ принадлежности. Иногда говорят: множество N содержит элемент 3, или 3 содержится вN, или 3 является элементом множестваN. Если элемент не принадлежит множеству, то при записи используют символ(символ отсутствия принадлежности). ЗаписьxА означает: элемент х принадлежит множеству А. Записьозначает, чтохне является элементом множества А.

Задать множество — значит указать каким-либо способом, из каких элементов это множество состоит.

Характеристическое свойство - это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.

Отношения между множествами

Существует пять типов отношений между множествами, которые наглядно при помощи особых чертежей, называемых кругами Эйлера:

1. Тождество, или взаимное включение множеств (А=В) (рис. 1).

2. Полное включение меньшего множества в большее (рис. 2).

3. Частичное включение одного множества в другое (рис. 3).

4. Полное включение одного или более множеств в одно большее универсальное множество (рис. 4, 5).

5. Полное взаимное исключение множеств (рис 6).

Множества А и В называют равными, если А  В и В  А. Если множества А и В равны, то записывают: А=В.

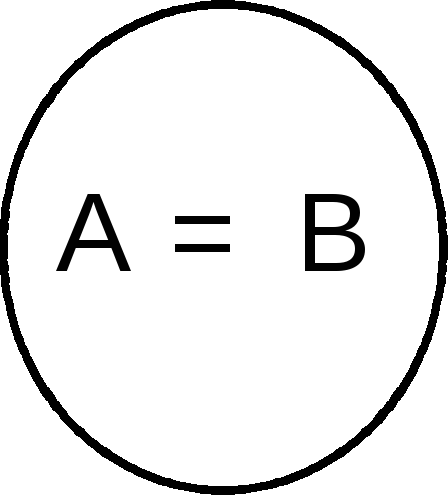
Рис.1. Тождество множеств.

Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А (рис. 2).

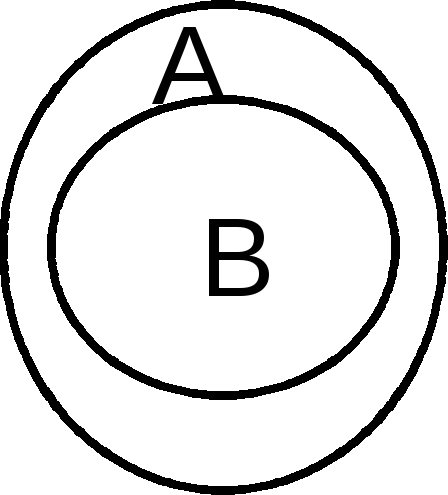
Рис. 2. Полное включение меньшего множества в большее.

Запись В А читают: "В - подмножество А", или "В включается в А". Среди всех подмножеств заданного множества А должно быть обязательно пустое множествои само множество А: (А и АА).

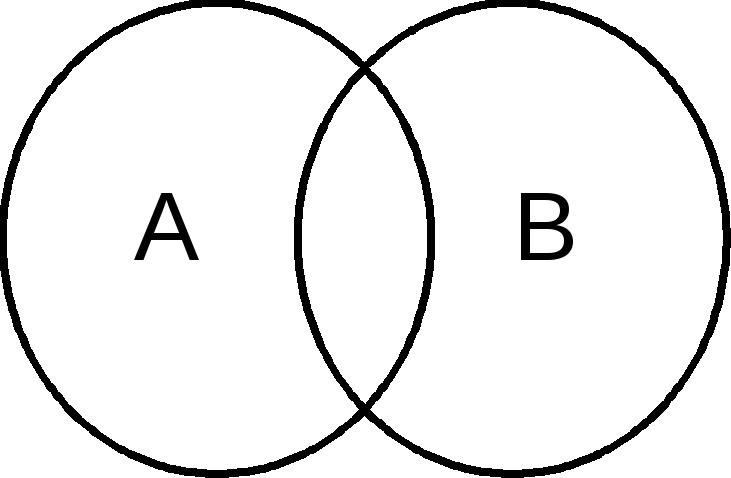
Рис.3. Частичное включение одного множества в другое.

Частичное включение одного множества в другое называют в теории множеств произведением множеств.

Говорят, что множества А и В пересекаются, если имеются общие элементы множеств А и В.

Обычно говоря о множестве, например о множестве фактов нарушения общественного порядка, краж, статистических данных и др., мы интересуемся только тем, из каких элементов оно состоит, и не думаем о порядке расположения элементов. Это обстоятельство находит свое отражение в определении равенства двух множеств.

Пусть U − теоретически мыслимое множество вариантов поведения личности. Р − множество вариантов поведения, доступных конкретному субъекту в конкретных условиях места и времени.(см. рис. 4). Q − множество вариантов поведения, запрещенных уголовным законом. Эти множества не совпадают, а могут пересекаться (см. рис. 5).

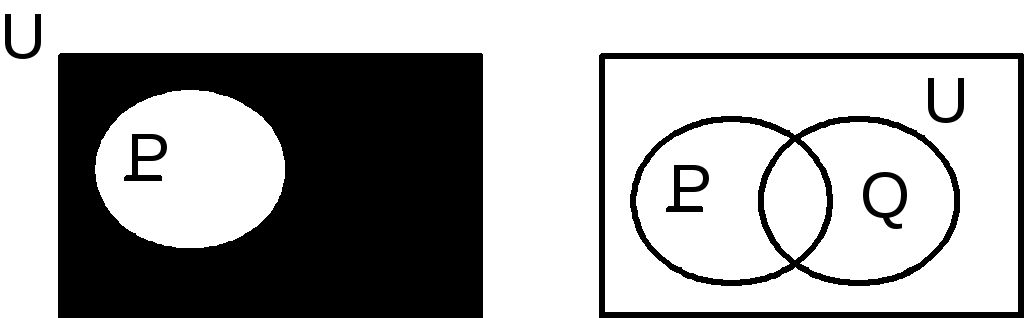
Рис. 4 Рис. 5.

На языке теории множеств это означает, что у обоих множеств есть общие элементы. Обозначим , R − зона запрета.

Если множества А и В не имеют общих элементов, то они не пересекаются (рис. 6).

Рис.6. Полное взаимное исключение множеств