Модуль 5. Элементы теории вероятностей.

Теоретические занятия (лекции) – 6 часов.

Лекция 11. (Информационная лекция с использованием средств мультимедиа).

Основные понятия и теоремы теории вероятностей.

Элементы комбинаторики. Сущность и условия применимости теории вероятностей. Испытания, события, виды случайных событий, полная группа событий. Частота и вероятность. Классическое и статистическое определения вероятности. Свойства вероятности.

Алгебра событий. Противоположные события. Условная вероятность. Основные формулы для вычисления вероятностей. Теоремы сложения вероятностей. Теоремы умножения вероятностей. Формула полной вероятности. Формулы Байеса. Схема независимых испытаний. Формулы Бернулли, Муавра-Лапласа, Пуассона.

На практике иногда приходится выбирать из некоторого конечного множества объектов подмножества элементов, обладающие теми или иными свойствами, располагать элементы в определенном порядке, подсчитывать число возможных подмножеств. Область математики, которая изучает задачи, связанные с оценкой количества возможных вариантов (комбинаций) называется комбинаторикой, а сами такие задачи – комбинаторными. Формулы для подсчета количества комбинаций, полученные в комбинаторике, используются в других разделах математики – теории вероятностей, задачах оптимизации, информатике.

Дадим математическую формулировку комбинаторной задачи. Для множества, содержащего k элементов, найти число всех возможных комбинаций (конструкций) из m элементов исходного множества, построенных указанным способом. Из этого определения вытекает, что в комбинации могут участвовать не все элементы исходного множества и что комбинации могут отличаться друг от друга и при одинаковых составах элементов, если это связано со способом построения комбинации.

Сформулируем два основных правила комбинаторики.

Правило суммы: Если первый элемент (а₁) можно выбрать n₁ способами, второй элемент а₂ можно выбрать другими n₂ способами, а элемент а₃ – отличными от первых двух n₃ способами и т.д. до элемента а_k , выбранного отличными от предыдущих n_k способами то выбор одного из элементов а₁ или а_{2 , …} или а_k может быть сделан N способами, где .

Правило произведения: Если первый элемент (а₁) можно выбрать n₁ способами, второй элемент а₂ можно выбрать другими n₂ способами, а элемент а₃ – отличными от первых двух n₃ способами и т.д. до элемента а_k , выбранного отличными от предыдущих n_k способами то выбор всех элементов (а₁, а₂, …а_k) в указанном порядке может быть сделан N способами, где .

Пусть n — натуральное число, n! (читается "эн-факториал") — это произве­дение 123...n.

Размещениями без повторений из k элементов по m называют упорядоченные m-элементные подмножества, полученные путем однократного выбора различных элементов из k-элементного исходного множества.

Число размещений без повторений из k элементов по m вычисляют по формуле

Перестановками без повторений из k элементов называются размещения из k элементов по k.

Сочетаниями из k элементов по m называются m-элементные подмножества, полученные путем однократного выбора различных элементов из k-элементного исходного множества. Число сочетаний из k элементов по m равно .

Размещениями с повторениями из k элементов по m называют упорядоченные m-элементные подмножества, полученные путем выбора элементов из k-элементного исходного множества, причем выбранные элементы могут повторяться.

Число размещений вычисляется по формуле:

Пусть в некотором множестве содержится k элементов, и при этом элемент а1 повторяется k1 раз, элемент а2 – k2 раз …аn – kn раз, . Все возможные упорядоченные последовательности из всех элементов этого множества называютсяперестановками с повторениями и обозначаются .

Различные составы последовательностей длины m, компоненты которых принадлежат k-элементному множеству, называют сочетаниями с повторениями. Число сочетаний с повторениями вычисляется по формуле

Случайные события

Теория вероятностей – это раздел математики, изучающий количественные закономерности случайных событий. Теория вероятностей, основанная еще в XVII веке, имеет важное значение в современной научной системе мира. Математические модели социологии, криминологии, макроэкономики и многих других наук базируются на вероятностных законах.

Под событием в теории вероятностей понимается всякий факт, который в результате действия (опыта, испытания) может произойти или не произойти.

События обозначаются большими латинскими буквами: A,B,C,D,E....

Несколько событий называются несовместными в некотором опыте, если никакие два из них не могут появиться вместе. В противном случае события называются совместными.

Множество событий − возможных исходов некоторого опыта, одно из которых в результате опыта обязательно происходит, а любые два из них несовместны, называется множеством элементарных событий или полной группой событий.

Каждый исход опыта представляется одним и только одним элементарным событием. Случайным событием называется любое подмножество полной группы событий данного опыта.

Несколько событий в данном опыте называются равновозможными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является более возможным, чем другое.

Два события называются зависимыми, если наступление одного из них влияет на возможность появления другого.

Два события называются независимыми, если наступление одного из них влияет на возможность наступления другого.

Примерами независимых событий являются несколько последовательных опытов подбрасывания монеты.

Определение вероятности

Случайное событие характеризуется свойством статистической устойчивости, которое тесно связано с понятием частоты наступления события.

Если в результате некоторого опыта событие наступало один или несколько раз, то отношение числа наступлений события к общему числу испытаний называется частотой наступления события.

Практика показывает, что частота наступления события мало и не систематически изменяется от одной серии опытов (подбрасываний) к другой, т.е. для событияхарактерна статистическая устойчивость − чем больше число опытов в серии, тем меньше колебания частоты.

Это означает, что при достаточно большом количестве опытов частота наступления случайного события будет колебаться около некоторого числа, называемого вероятностью события.

Статистическое определение вероятности:

Вероятность – это число, которое получается как предел частоты наступления события при неограниченном увеличении числа испытаний.

.

Здесь N – число испытаний (опытов);

M – число событий А, наступивших при этих испытаниях.

Слабым местом такого определения вероятности является то, что нельзя провести бесконечное количество опытов, да еще в одинаковых условиях, обеспечивающих статистическую устойчивость. Следовательно, необходимо обходится ограниченным количеством опытов и вместо вероятности пользоваться частотой.

Если есть основания полагать, что случайные события равновозможны и несовместны, то можно воспользоваться так называемым классическим определением вероятности.

Пусть множество исходов опыта состоит из n равновозможных и несовместных исходов. Если m из них благоприятствуют наступлению события , то вероятностью событияназывается число:

.

Здесь P(A) − обозначение вероятности события A.

Вероятность события, вычисленная по предложенным формулам, всегда есть правильная дробь, поэтому:

.

Событие, которое непременно произойдет в результате опыта, называется достоверным. Вероятность достоверного события равна единице.

Невозможным называется событие, которое заведомо не может произойти в результате опыта. Вероятность невозможного события равна нулю.

Действия над событиями

Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В:

.

Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Суммой двух событий иназывается событие, состоящее в выполнении событияили события, или обоих вместе:

.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Если сумма двух событий – достоверное событие, а их произведение – невозможное событие, то эти события называются противоположными. Противоположные события будем обозначать и.

Пример 8. По мишени производят три выстрела.

Теоремы сложения вероятностей

Теорема. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. Р(А+В)=Р(А)+Р(В).

Теорема. Если события А1, …, Аn попарно несовместны, то вероятность суммы событий равна сумме вероятностей этих событий. Р(А1+… + Аn )=Р(А1)+… +Р(Аn).

Теорема. Если события А1, …, Аn образуют множество элементарных событий, то сумма их вероятностей равна единице. Р(А1)+… +Р(Аn)=1.

Теорема. Сумма вероятностей двух противоположных событий равна единице. Р(А)+Р()=1.

Теорема умножения вероятностей

Теорема. Вероятность совместного наступления двух событий равна произведению вероятности наступления первого события на условную вероятность наступления второго события, вычисленную в предположении, что первое событие имеет место.

Если события А и В независимы, то

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Р(А+В)=Р(А)+Р(В)-Р(АВ).

Формула полной вероятности

Теорема. Вероятностью события А, которое может наступить лишь при условии появления одного из N попарно несовместных событий В1, В2, …Вn, образующих множество элементарных событий, равна:

А– событие, вероятность которого определяется.

Р(Вi) – вероятность появления случая номер «i».

N – количество возможных случаев.

Р(А/Вi) – вероятность появления события А в ситуации, когда наблюдается случай номер «i» (условная вероятность).

Формула Байеса

Теорема. Пусть зафиксировано появление события А, известны вероятности наступления несовместных событий В1, В2, …Вn. Тогда условные вероятности равны:

А– событие, которое произошло.

Р(Вi) – вероятность появления случая номер «i».

N – количество возможных случаев.

Р(Вi/А) – искомая вероятность того, что имел место случай Вi, при условии, что произошло событие А.

Р(А/Вi) – вероятность появления события А в ситуации, когда наблюдается случай номер «i» (условная вероятность).

Задачи, в которых используется эта формула предполагают, что имел место некоторый факт, который мог быть проявлением одного из взаимоисключающих случаев (событий). Требуется выяснить вероятности случаев, предшествующих этому факту.

Лекция 12. (Информационная лекция с использованием средств мультимедиа).

Случайные величины. Дискретная случайная величина и ее характеристики.

Вероятностное пространство. Понятие случайных величин, их виды и способы их описания. Закон распределения дискретной случайной величины. Многоугольник распределения. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия и среднее квадратическое отклонение. Свойства математического ожидания и дисперсии. Система двух случайных величин.

Биномиальный закон распределения случайной величины, вычисление его основных характеристик.

Случайная величина

Случайные события в ряде задач теории вероятностей связываются с числовыми величинами. В качестве примеров числовых величин можно использовать следующие: число попаданий в мишень, число выигрыша в лотерею, число вызовов, поступающих на телефонную станцию, число дорожно-транспортных происшествий. Случайное событие представляет собой подмножество множества элементарных событий. Случайная величина – функция, заданная на множестве элементарных исходов опыта, принимающая в результате опыта одно из своих числовых значений.

Все многообразие числовых величин можно условно разделить на случайные, определенные и неопределенные.

Случайные величины будем обозначать прописными буквами X, Y, Z , а их возможные значения − соответствующими строчными буквами x, y, z. Например, если случайная величина Х имеет три возможных значения, то они будут обозначены так: . В данном опыте случайная величина принимает значения, гдеи. Итак, случайная величина − это величина, которая в результате опыта принимает одно из своих значений.

Для случайных событий характерна статистическая устойчивость. При многократном повторении наблюдений частота появления каждого из возможных значений случайной величины будет мало и не систематически изменяться.

Неопределенными величинами называют такие величины, которые принимают значения в зависимости от случая, но которые нельзя многократно наблюдать в однородных условиях или считать их статистически устойчивыми.

Различают случайные величины дискретного и непрерывного типа. Случайная величина, принимающая различные целые значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной. Если случайная величина принимает значения, которые могут отличаться друг от друга на сколь угодно малое число, то ее называют непрерывной случайной величиной.

Закон распределения случайной величины

Дискретная случайная величина считается теоретически заданной, если известны все возможные значения, которые принимает эта величина и вероятности, с которыми она принимает эти значения, т.е. если дана таблица или ряд распределения.

Х=хi	Х1	х2	х3	...				...	хn
P(X=xi)	P1	P2	P3	...				...	Pn

В верхней строке выписываются все возможные значения x1, x2, x3, … xn величины Х, в нижней строке выписываются вероятности р1, р2, р3,...., рn значений x1, x2, x3, … xn. Читается таблица следующим образом: случайная величина Х может принять значение xi с вероятностью .

Так как в результате испытания величина Х всегда примет одно из значений x1, x2, x3, … xn, то

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину Х будем говорить, что она подчинена данному закону распределения.

Дискретная случайная величина Х называется распределенной по биномиальному закону, если свои возможные значения 0,1,2,...,n она принимает с вероятностями, которые подсчитываются по формуле Бернулли.

.

Геометрическое изображение ряда распределения называется многоугольником распределения.

Функция распределения случайной величины

Для непрерывной случайной величины нельзя построить таблицу распределения. Действительно, непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток. Составить таблицу, в которой были бы перечислены все возможные значения такой случайной величины, невозможно. Закон распределения непрерывной случайной величины представляют с помощью функции распределения случайной величины.

Для количественной характеристики распределения непрерывной случайной величины удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где x-некоторая текущая переменная. Вероятность этого события, тем больше, чем больше х, то есть является некоторой функцией от х.

Пусть Х − непрерывная случайная величина с возможными значениями из некоторого интервала (а;b) и х − действительное число. Под выражением Х<х понимается событие “случайная величина Х приняла значение, меньшее х”. Вероятность этого события Р(Х<х) есть некоторая функция переменной х.

Функцией распределения вероятностей случайной величины Х называется вероятность того, что случайная величина Х примет значение, меньшее х, где х − любое действительное число, т.е.

F(x)=P(X<x).

Функцию распределения F(x) иногда называют интегральным законом распределения.

Отметим, что функция распределения точно также определяется для дискретных случайных величин, поэтому она является универсальной характеристикой случайной величины.

Для дискретной случайной величины функция распределения

.

Случайная величина Х − непрерывна, если непрерывна ее функция распределения F(x).

Сформулируем некоторые общие свойства функции распределения.

1. 0 F(x) 1. Это свойство следует из того, что F(x) есть вероятность.

2. F(x) − есть неубывающая функция.

3. F(-)=0, F(+)=1.

Зная ряд распределения дискретной случайной величины, можно легко построить функцию распределения этой величины. Когда текущая переменная х проходит через какое-нибудь из возможных значений величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.

Числовые характеристики дискретной случайной величины

Математическое ожидание

Математическое ожидание дискретной случайной величины – сумма произведений всех ее возможных значений на их вероятности.

Математическое ожидание приближенно равно среднему значению случайной величины.

Свойства математического ожидания.

1. М(С)=С.

2. М(X+Y)=M(X)+M(Y).

3. M(XY)=M(X)M(Y).

Дисперсия, среднеквадратическое отклонение

Иногда математическое ожидание случайной величины не дает ее исчерпывающей характеристики. В некоторых случаях требуется знать сколь велики отклонения отдельных значений с.в. от ее математического ожидания.

Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

На дисперсию распространяются все свойства математического ожидания (поскольку она является математическим ожиданием квадрата отклонения случайной величины).

Среднеквадратическим отклонением случайной величины называется арифметическое значение квадратного корня из дисперсии этой случайной величины

.

Лекция 13. (Информационная лекция с использованием средств мультимедиа).

Непрерывные случайные величины.

Непрерывные случайные величины. Функция распределения и ее свойства. Плотность распределения вероятностей и ее свойства. Числовые характеристики непрерывной случайной величины.

Законы распределения непрерывной случайной величины: равномерный, нормальный, их особенности. Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях.

Случайная величина х называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси.

Для непрерывной случайной величины х при любом х₀  R имеет место равенство

P(х = х₀) = 0, (1)

а также

P(х₁  х  х₂ ) = P(х₁ < х < х₂ ) = P(х₁ < х  х₂ ) = P(х₁  х < х₂ ) = F(х₂ ) - F (х₁ ), (2)

где F(x) функция распределения величины х.

Пусть f(x) - неотрицательная интегрируемая функция, определенная на всей числовой оси и удовлетворяющая условию

. (3)

Тогда функция

(4)

обладает всеми свойствами функции распределения. Кроме того, F(x) непрерывна в любой точке (и слева, и справа). Следовательно, случайная величина х, определяемая функцией распределения F(x), является непрерывной.

Мы говорим, что случайная величина х с функцией распределения F(x) раcпределена с плотностью, если существует неотрицательная функция f(x), такая, что для любого х  R имеет место равенство (2). При этом f(x) называется плотностью вероятности случайной величины х, а ее график – кривой распределения.

Из определения плотности вероятности f(x) и свойств функции распределения следует, что f(x) должна удовлетворять условию (1). И обратно, если f(x)  0 и выполняется условие (1), то f(x) является плотностью вероятности.

Если случайная величина х имеет плотность вероятности f(x) , то имеет место формула

р(х₁  х  х₂ ) = .

Для непрерывной случайной величины математическое ожидание, дисперсия и среднее квадратическое отклонение определяются следующим образом:

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей. Во-первых, это наиболее часто встречающийся на практике закон распределения непрерывных случайных величин. Во-вторых, он является предельным законом, в том смысле, что к нему при определенных условиях приближаются другие законы распределения.

Нормальный закон распределения характеризуется следующей формулой для плотности вероятности:

,

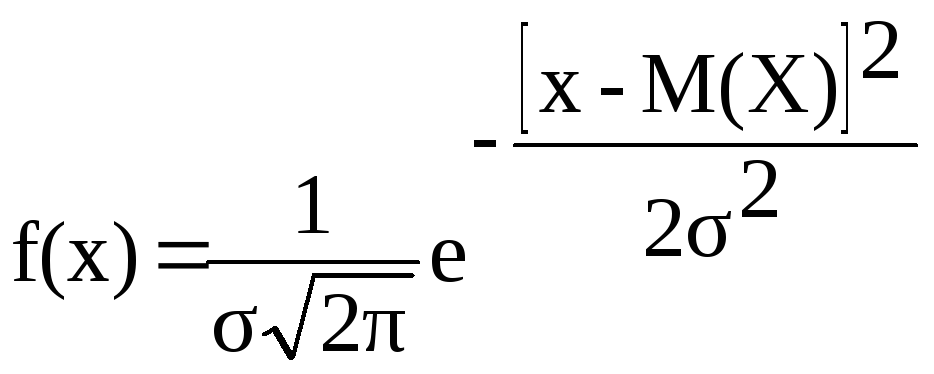Здесь х - текущие значения случайной величиныX, а М(X) и  - ее математическое ожидание и стандартное отклонение, которые полностью определяют функцию f(x). Таким образом, если случайная величина распределена по нормальному закону, то достаточно знать только два числовых параметра: М(Х) и , чтобы полностью знать закон ее распределения. График функции называется нормальной кривой распределения (кривой Гаусса). Он имеет симметричный вид относительно ординаты х = М(Х). Максимальная плотность вероятности, равная  , соответствует математическому ожиданиюХ=М(Х), и по мере удаления от нее плотность вероятности f(х) симметрично спадает, постепенно приближаясь к нулю (см. рис.)

Практические и семинарские занятия – 14 часов.

Занятие 23. Комбинаторика.

Форма проведения занятия – краткое обсуждение теоретического материала, решение задач.

Отрабатываемые вопросы:

1. Решение простейших комбинаторных задач методом перебора и с помощью графов.

2. Решение комбинаторных задач по формулам.

3. Решение более сложных комбинаторных задач.

Занятие 24. Определение вероятности. Теоремы сложения, умножения вероятностей.

Форма проведения занятия – проверка домашнего задания, краткое обсуждение теоретического материала, решение задач.

Отрабатываемые вопросы:

1. Решение задач на классическое определение вероятности.

2. Решение задач с помощью теорем сложения, умножения вероятностей.

Занятие 25. Формула полной вероятности. Формулы Байеса.

Форма проведения занятия – проверка домашнего задания, краткое обсуждение теоретического материала, решение задач.

Отрабатываемые вопросы:

1. Решение задач с помощью формулы полной вероятности

2. Решение задач с помощью формул Байеса.

Занятие 26. Формулы Бернулли, Муавра-Лапласа, Пуассона.

Форма проведения занятия – проверка домашнего задания, проведение самостоятельной работы по теме «Основные понятия и теоремы теории вероятностей», обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Решение задач с помощью формул Бернулли, Муавра-Лапласа, Пуассона.

Занятие 27. Дискретные случайные величины и их числовые характеристики.

Форма проведения занятия – проверка домашнего задания, обсуждение результатов самостоятельной работы, обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Решение задач на нахождение закона распределения дискретной случайной величины.

2. Построение многоугольника распределения дискретной случайной величины.

3. Нахождение числовых характеристик дискретной случайной величины: математического ожидания, дисперсии и среднего квадратического отклонения.

4. Биномиальный закон распределения случайной величины

Занятие 28. Непрерывные случайные величины и их числовые характеристики.

Форма проведения занятия – проверка домашнего задания, обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Построение функции распределения случайной величины.

2. Построение графика плотности распределения вероятностей.

3. Нахождение числовых характеристик непрерывной случайной величины.

4. Законы распределения непрерывной случайной величины: равномерный, нормальный.

Занятие 29. Контрольная работа № 5 по теме «Элементы теории вероятностей».

Форма проведения занятия – проверка домашнего задания, проведение контрольной работы № 5 по теме «Элементы теории вероятностей».

Управление самостоятельной работой студента.

Консультации, опрос по теоретическому материалу, проверка и разбор домашней работы, а также результатов самостоятельной и контрольной работы (см. подробнее в Приложении 3).