
- •Операции над множествами
- •Основные свойства функций.
- •Основные элементарные функции. Их свойства и графики
- •1. Линейная функция.
- •Свойства линейной функции
- •2. Квадратичная функция.
- •3. Показательная функция.
- •4. Логарифмическая функция
- •6. Степенная функция
- •Пример использования функций в экономике.
- •Предел функции в бесконечности и точке
- •Теоремы о пределах функций
- •Два замечательных предела
- •Свойства функций, непрерывных в точке
- •Классификация точек разрыва функций
- •Определение производной
- •Геометрический смысл производной
- •Производная сложной функции
4.3. Вопросы к экзамену в первом семестре. Математика
Матрицы, операции над матрицами
Прямоугольной матрицей размерностью m на n называется прямоугольная таблица, состоящая из m строк и n столбцов
Виды матриц: Квадратная,Еденичная,Нулевая, матрица-строка(матрица-столбец).
Операции над матрицами:Умножение М на число,умножение Мна М,Сложение М,Разность М,Возведение в степень М.Транспонирование М,След М.
След матрицы. Свойства следа матрицы.
Следом квадратной матрицы называется сумма ее диагональных элементов. След обозначается trA и играет важную роль в исследовании матриц и их приложениях.
Свойства следа матрицы:
При транспонировании матрицы ее след не изменяется
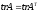 .
.Если матрица D диагональная с элементами
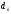 (
(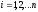 ),
то для любого натуральногоm
),
то для любого натуральногоm
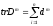 .
.Если А и В квадратные матрицы n-го порядка, то
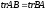 (хотя в общем случае
(хотя в общем случае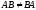 ).
).Если С невырожденная матрица n-го порядка, то для любой матрицы А n-го порядка выполняется равенство
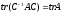 .
.
Определители. Вычисление определителей. Свойства определителей.
является определитель,
который для матрицы
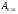 обозначается
следующим образом:
обозначается
следующим образом:
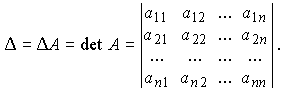
Определитель
матрицы первого порядка
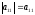 .
.
Определитель
матрицы второго порядка равен
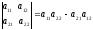 .
.
определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.
Определитель матрицы третьего порядка равен
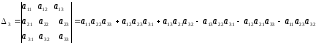 .
.
Свойства определителей
Перечисленные ниже свойства рекомендуется использовать при вычислении определителей.
1. Если в определителе есть нулевая строка (столбец), то определитель равен нулю.
2. Общий множитель любой строки (столбца) можно выносить за знак определителя.
3. При транспонировании матрицы ее определитель не меняется.
4. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
5. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
6. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
7.
Сумма произведений элементов какой-либо
строки (столбца) матрицы на алгебраические
дополнения элементов другой стоки
(столбца) этой матрицы равна нулю, т. е.
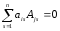 при
при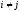 .
.
8. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то величина определителя не изменится.
9.
Сумма произведений произвольных чисел
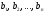 на алгебраические дополнения элементов
любой строки (столбца) равна определителю
матрицы, полученной из данной матрицы
заменой элементов этой строки (столбца)
на числа
на алгебраические дополнения элементов
любой строки (столбца) равна определителю
матрицы, полученной из данной матрицы
заменой элементов этой строки (столбца)
на числа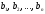 .
.
10.
Определитель произведения двух квадратных
матриц равен произведению их определителей:
 ,
где С=АВ. А и В – матрицы n-го порядка.
,
где С=АВ. А и В – матрицы n-го порядка.
Обратная матрица. Вычисление обратной матрицы.
Опр. Матрица A-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица: A-1A = A A-1 = E. Обратная матрица может существовать только для квадратной матрицы
Сформулируем правило нахождения обратной матрицы.
1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A-1 существует.
2. Транспонируем матрицу А и получим АT.
3. Составим
присоединенную матрицу
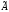 алгебраических дополнений элементов
матрицы АT.
алгебраических дополнений элементов
матрицы АT.
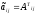 .
(т.е. в матрице
.
(т.е. в матрице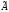 элементомi
- ой строки и j
- го столбца будет алгебраическое
дополнение
элементомi
- ой строки и j
- го столбца будет алгебраическое
дополнение
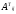 элемента
элемента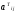 матрицы АT.
матрицы АT.
4. Найдем обратную
матрицу
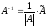 .
.
После вычисления обратной матрицы рекомендуется убедиться в том, что выполняется одна из частей условия.
![]()
Ранг матрицы. Элементарные преобразования матрицы.
Рангом матрицы А (обозначается r(A)) называется наивысший порядок отличных от нуля миноров этой матрицы.
Из определения следует:
Ранг матрицы
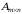 не
превосходит меньшего из ее размеров,
т.е.
не
превосходит меньшего из ее размеров,
т.е.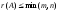 ;
;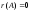 тогда
и только тогда, когда все элементы
матрицы равны нулю
тогда
и только тогда, когда все элементы
матрицы равны нулю
Элементарные преобразования матрицы:
отбрасывание нулевой строки (столбца);
умножение всех элементов строки (столбца) на число, не равное нулю;
перестановка строк (столбцов) матрицы;
прибавление к каждому элементу строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
транспонирование.
Системы линейных уравнений. Теорема Крамера.
Системы линейных уравнений
Система m линейных уравнений с n переменными имеет вид
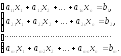 (1)
(1)
Здесь x1, x2,...xn –
неизвестные, коэффициенты aij
и свободные члены
 -
известные числа.
-
известные числа.
Более кратко
систему можно записать:
 .
.
Систему линейных
уравнений можно записать и в матричной
форме:
 .
.
где
 ,
,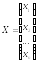 ,
, .
.
Решением системы называется любой упорядоченный набор чисел, при подстановке которых вместо неизвестных каждое уравнение системы обращается в тождество.
Система называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.
Система называется определенной, если она имеет единственное решение и неопределенной, если решений больше одного.
Система линейных уравнений может иметь:
единственное решение (система совместна и определена);
более одного решения (система совместна и неопределена);
не иметь решений (система несовместна).
Две системы называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.
Формулы Крамера.
Теорема.
Пусть
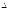 - определитель матрицы системы А, а
- определитель матрицы системы А, а - определитель матрицы, получаемой из
матрицы А заменой j-го столбца столбцом
свободных членов. Тогда, если
- определитель матрицы, получаемой из
матрицы А заменой j-го столбца столбцом
свободных членов. Тогда, если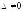 ,
то система имеет единственное решение,
определяемое по формулам:
,
то система имеет единственное решение,
определяемое по формулам: (
( ).
).
7. Решение систем линейных уравнений методом обратной матрицы.
Матричный метод
Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная).
Решение системы можно получить так:
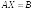 ,
,
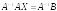 ,
(обратная матрица существует, так как
,
(обратная матрица существует, так как
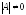 .
.
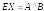 ,
,
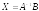 .
.
Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.
Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.
Решение систем линейных уравнений методом Гаусса.
Метод Гаусса.
Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.
Метода Гаусса – метод последовательного исключения неизвестных. Его суть заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.
Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:
- перестановка местами двух уравнений;
- умножение обеих частей одного из уравнений на любое число, отличное от нуля;
- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.
9. Системы линейных однородных уравнений. Фундаментальная система реше-ний.
Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:
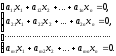 (2)
(2)
Система линейных однородных уравнений всегда совместна и имеет хотя бы одно решение x1 = x2 = ... = xn = 0. Это решение не всегда единственно.
Система
линейных однородных уравнений имеет
ненулевые решения тогда и только тогда,
когда ранг ее матрицы коэффициентов
при переменных меньше числа переменных,
т.е.
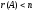 .
.
Обозначим
решение системы
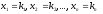 в виде строки
в виде строки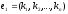 .
.
Система
линейно независимых решений
 называетсяфундаментальной,
если каждое решение системы (2) является
линейной комбинацией решений
называетсяфундаментальной,
если каждое решение системы (2) является
линейной комбинацией решений
![]() .
.
Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (2) меньше числа переменных n , то всякая фундаментальная система решений системы (2) состоит из n-r решений.
Поэтому
общее
решение системы
(2) линейных однородных уравнений имеет
вид
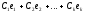 ,
где
,
где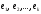 любая фундаментальная система решений,
любая фундаментальная система решений,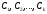 - произвольные числа, k=n-r.
- произвольные числа, k=n-r.
Для нахождения фундаментальной системы решений системы уравнений (2) ее r базисных переменных выражают через свободные переменные. Затем поочередно заменяют n-r свободных переменных элементами каждой строки невырожденной квадратной матрицы порядка n-r, например единичной.
Теорема. Общее
решение системы (1) m линейных уравнений
с n переменными равно сумме общего
решения соответствующей ей системы
однородных линейных уравнений (2) и
произвольного частного решения системы:
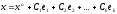 ,
где
x
и
,
где
x
и
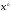 соответственно
общее и частное решения системы (1),
соответственно
общее и частное решения системы (1),
 - фундаментальная
система решений.
- фундаментальная
система решений.
10.Векторы на плоскости и в пространстве и действия над ними.
Вектором называется
направленный отрезок
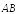 с начальной точкой А и конечной точкой
В. Обозначается вектор одной буквой
с начальной точкой А и конечной точкой
В. Обозначается вектор одной буквой![]() или
или![]() Векторы
характеризуются длиной
Векторы
характеризуются длиной![]() и
направлением. Длиной вектора
и
направлением. Длиной вектора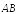 называется число, равное длине отрезка
АВ.
называется число, равное длине отрезка
АВ.
Векторы, лежащие
на одной прямой или на параллельных
прямых, называются коллинеарными
![]() .
.
Если начало и конец
вектора совпадают, то такой вектор
называют нулевым и обозначают
 .
Так как направление нулевого вектора
произвольно, то считают, что он коллинеарен
любому вектору.
.
Так как направление нулевого вектора
произвольно, то считают, что он коллинеарен
любому вектору.
Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.
Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.
Произведением
вектора
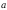 на действительное число
на действительное число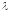 называется вектор
называется вектор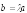 ,
имеющий длину
,
имеющий длину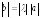 ,
направление которого совпадает с
направлением вектора
,
направление которого совпадает с
направлением вектора ,
если
,
если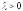 и противоположно ему, если
и противоположно ему, если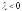 .
.
Вектором,
противоположным вектору
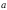 ,
называется вектор
,
называется вектор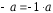
Действия над ними:Сложение векторов,Вычитание векторов,Произведение векторов,
11. Уравнение линии на плоскости. Уравнение прямой.
. Cвязь y = f(x) или F(xy) = 0 называется уравнением линии L, если этим соотношениям удовлетворяют координаты любой точки линии L и не удовлетворяют координаты точек, не принадлежащих линии L.
Общее уравнение прямой.
Рассмотрим уравнение
Ax + By + С = 0, (5)
в котором А и В не равны нулю одновременно.
При любых значениях коэффициентов А, В (не равных одновременно нулю) и С уравнение (5) есть уравнение некоторой прямой на плоскости Оxy, его называют общим уравнением прямой.
Заметим, что в отличие от уравнения пучка прямых общее уравнение включает и уравнение любой вертикальной прямой, параллельной оси Oy.
12. Условие параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
Равенство угловых
коэффициентов является необходимым и
достаточным условием параллельности
прямых.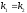 ,
если прямые заданы общими уравнениями,
то
,
если прямые заданы общими уравнениями,
то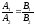 Для
перпендикулярности
Для
перпендикулярности
прямых необходимо
и достаточно, чтобы выполнялось равенство:
 .если
прямые заданы общими уравнениями, то
.если
прямые заданы общими уравнениями, то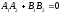
Расстояние от точки до прямой.
Пусть даны точка
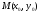 и прямая
и прямая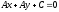 .
Под расстоянием от точки до прямой
понимается длина перпендикуляра,
опущенного из этой точки на прямую. Она
находится по формуле:
.
Под расстоянием от точки до прямой
понимается длина перпендикуляра,
опущенного из этой точки на прямую. Она
находится по формуле:
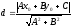 .
.
13. Уравнение плоскости. Условия параллельности и перпендикулярности плос-костей.
14. Прямая в пространстве. Условия параллельности и перпендикулярности пря-мых в пространстве.
15. Взаимное расположение прямой и плоскости в пространстве. 16. Применение методов линейной алгебры при решении задач с экономическим содержанием.
17. Понятие множества, операции над множествами. Числовые множества.
Множество - это совокупность объектов произвольной природы. Элемент множества – это объект, принадлежащий данному множеству.
Операции над множествами
Операции над множествами:
Пересечение множеств.
Объединение множеств.
Разность множеств.
Пересечением множеств А и В называется множество, содержащие только такие элементы, которые принадлежат множеству А и множеству В.
Обозначение
данной операции: Р=А
 В.
В.
Если изобразить множество А и В при помощи кругов Эйлера, то пересечение данных множеств изобразиться заштрихованной областью.
Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из этих множеств.
Согласно
определению объединения:
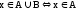 или
или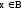 .
Аналогично для пересечения:
.
Аналогично для пересечения: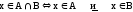 .
.
Операцию, при помощи которой находят объединение множеств называют объединением, пересечение - пересечением.
Пусть
B
– подмножество множества А. Множество
всех элементов из А, не принадлежащих
множеству В, называют дополнением к
подмножеству В и обозначают
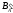 .
.
Разностью
двух множеств А и В (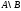 )называется
множество, в которое входят те элементы,
которые принадлежат А и не принадлежат
В.
)называется
множество, в которое входят те элементы,
которые принадлежат А и не принадлежат
В.
18. Функция одной переменной. Основные свойства функции.
1.1. Понятие функции одной переменной
Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.
Таким образом, задать функцию, значит задать три объекта:
1) множество Х (область определения функции);
2) множество Y (область значений функции);
3) правило соответствия f (сама функция).
Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x3. В этом случае правилоf есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x3 само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x) =x3 принимает значение у= f(2) =23 =8.
1.2. Способы задания функции одной переменной
Существуют несколько способов задания функции.
Аналитический способ. Функция f задается в виде формулы y=f(x). Например, y=3cos(x)+2x2. Этот способ является преобладающим в математических исследованиях и подробно рассматривается в классическом курсе математики. В географических исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.
Графический способ. На метеорологических станциях можно наблюдать работу приборов-самописцев, регистрирующих величины атмосферного давления, температуры воздуха, его влажности в любой момент времени суток. По полученному графику можно определить значения указанных величин в любой момент времени. Графиком функции y=f(x) называется множество всех точек плоскости с координатами (x, f(x)). График содержит всю информацию о функции. Имея перед собой график, мы как бы "видим функцию".
Табличный способ. Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x), соответствующие каждому х. Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.
Функция - это одно из важнейших математических понятий. Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.
