1.3. Поняття загального, часного й базисного рішень

Нехай система (І.І) представлена в жордановій формі (1.2). Виразимо базисні змінні через вільні.

(1.6)

(1.6) називається загальним рішенням системи (I.I).

Якщо вільним змінним додати будь-які числові значення й обчислити значення базисних змінних із системи (1.6), то вийде рішення вихідної системи, яке має назву часне. Часне рішення називається базисним, якщо вільні змінні приймають нульові значення. Рішення (1.3) є базисним.

У прикладі загальне рішення таке:

а базисне рішення . Якщо в жордановій формі число рівнянь дорівнює числу змінних n, тобто жорданова форма має вигляд:

то система має єдине рішення; воно є й загальним, і часним , і базисним. Якщо ж k‹n , тобто жорданова форма містить вільні змінні, то система має нескінченно багато рішень.

2. Загальні властивості задач лінійного програмування

2.І. Приклад задачі лінійного програмування - задача про використання обладнання

Підприємство випускає два види виробів А і В, для виробництва яких використовуються три типи верстатів. Відомі витрати часу (у годинах) верстатами на виробництво одиниці кожного виду виробів, резерви часу верстатів, а також прибуток від реалізації кожного виду виробу. Всі ці дані наведені в таблиці:

Таблиця 2.1.

Вироби верстати	А	В	Резерви часу (у годинах)
I	Витрати часу на виробництво одиниці виробу (у годинах)		Резерви часу (у годинах)
I	2	3	30
II	4	2	40
III	3	4	60
Прибуток від реалізації од. виробу	6	7

Потрібно скласти план виробництва виробів А і В, що забезпечує максимальний прибуток від їхньої реалізації.

Це приклад оптимізаційної економічної задачі. Вирішення таких задач містить наступні етапи:

побудова економіко-математичної моделі;

вирішення отриманої математичної задачі яким-небудь математичним методом;

впровадження результату вирішення в практику.

Під економіко-математичною моделлю розуміється система математичних співвідношень, що описує економічний процес.

Побудуємо економіко-математичну модель задачу про використання обладнання.

Нехай х₁ - кількість виробів А, а - кількість виробів В, які будуть випущені підприємством. Тоді прибуток, отриманий підприємством, дорівнює , Зміннііпотрібно підібрати так, щоб функціямаксимізувалася. Оскільки перший верстат може працювати не більше 30 годин, то повинно виконуватися співвідношення. Аналогічні обмеження на змінні х₁ і х₂накладаються резервами часу другого й третього верстатів. З огляду на те, що змінні х₁ і х₂ можуть приймати тільки додатні значення, одержимо наступну економіко-математичну модель задачі:

max

при обмеженнях

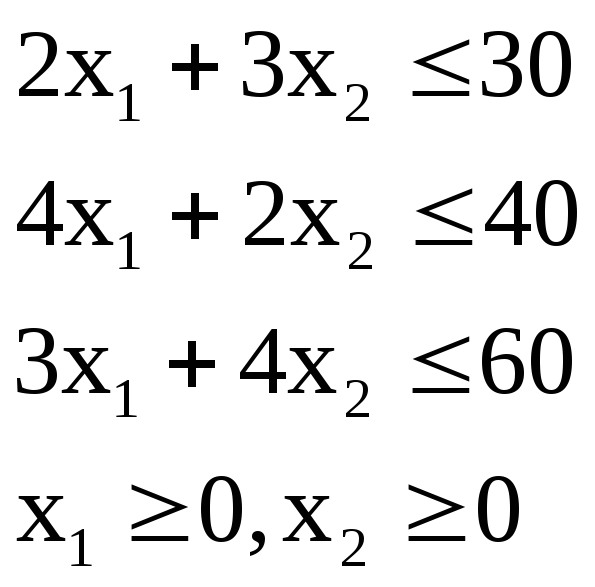
2.2. Задача про використання сировини

З математичної точки зору ця задача є узагальненням тієї, котра розглянута в попередньому параграфі. Формулюється вона так.

Підприємство випускає продукцію n видів , на виготовлення якої витрачається сировина m видів, запаси котрої на підприємстві дорівнюють відповідно . Відомі витратисировини S_i на виробництво одиниці продукції (i = ; j =). Вартість одиниці продукціїдорівнює(j =). Потрібно скласти такий план випуску продукції, при якому прибуток від реалізації продукції був би найбільшим.