3.8. Виродженість опорного плану. Зациклення

Опорний план ЗЛП називається виродженим, якщо деякі з базисних змінних приймають значення 0. У цьому випадку при переході від одного плану до іншого може не відбутися зменшення цільової функції.

Приклад. Нехай табличний вигляд ЗЛП такий:

Складемо першу симплекс-таблицю (таблиця 3.22).

Таблиця 3.22

Б					Q
	1	0	1	-1	0
	0	1	2	3	10
f	0	0	2	1	4

Опорний план, що відповідає цій симплекс-таблиці, є виродженим, тому що значення базисної змінної дорівнює 0. Перейдемо до нової симплекс-таблиці (табл.3.23)

Таблиця 3.23

Б					Q
	1	0	1	-1	0
	-2	1	0	5	10
f	-2	0	2	3	4

При новому опорному плані значення цільової функції залишилося колишнім: f=4.

При вироджених опорних планах можлива ситуація, коли, послідовно переходячи від одного опорного плану до іншого, через певну кількість кроків можна повернутися до колишнього опорного плану, так і не досягши мінімуму функції. Це називається зацикленням.

На практиці зациклення зустрічається вкрай рідко. Існує така модифікація симплекс-алгоритму, при якій зациклення виключається. Для практичних цілей достатня й наступна рекомендація: якщо відбулося зациклення, то з першою ж нагодою потрібно інакше вибрати генеральний елемент, ніж це робилося в перший раз.

Справедлива теорема про кінцевість симплекс-алгоритму: якщо ЗЛП розв'язна, то оптимальне рішення завжди може бути знайдене за допомогою симплекс-методу, причому починати можна з будь-якого опорного плану.

4. Двоїстість у лінійному програмуванні

1. Економічна інтерпретація двоїстих завдань

Поняття двоїстості в лінійному програмуванні викликає великий теоретичний і практичний інтерес. Двоїста задача - це допоміжна задача лінійного програмування, що формулюється за допомогою певних правил безпосередньо з умов вихідної, або прямої задачі.

Розглянемо практичну ситуацію, що приводить до необхідності розгляду двоїстої задачі.

Підприємство випускає чотири види продукції, для виготовлення якої використовується сировина трьох видів. Запаси сировини, норми витрати сировини на одиницю продукції й прибуток від реалізації одиниці продукції наведені в наступній таблиці:

Сировина	Види продукції				Запаси сировини
	П 1	П 2	П 3	П 4
	Норми витрати сировини
1	2	5	5	3	80
2	7	2	3	4	90
3	5	4	6	7	100
Прибуток	14	10	15	12

Потрібно скласти такий план виробництва продукції, при якому сумарний прибуток був би найбільшим.

Для запису математичної моделі задачі позначимо через x_j кількість продукції П_j (j=1, 2, 3, 4). Математична модель задачі:

Сформулюємо тепер двоїсту задачу. Припустимо , що деяка організація вирішила купити у підприємства всю сировину. Покупець прагне установити ціни у_i на одиницю сировини i-ro виду (i = 1, 2, 3, 4) так, щоб мінімізувати сумарну вартість сировини, що виражається величиною φ=80у₁+90у₂+100у₃. При цінах, запропонованих покупцем, підприємство одержить за сировину, витрачену на виготовлення продукції П₁, виторг 2y₁+7у₂+5у₃. Підприємство погодиться на угоду з покупцем, якщо цей виторг буде не менше прибутку підприємства від виготовлення одиниці продукції П₁, тобто якщо буде виконуватися умова 2y₁+7у₂+5у₃≥14. Такого ж обмеження покупець змушений ураховувати й для всіх інших видів продукції. Таким чином, математична модель задачі, розв'язуваної покупцем, має вигляд:

Отримана задача є двоїстою для вихідної.

З економічної точки зору зрозуміло, що f_max=φ_min. Дійсно, у випадку f_max>φ_min підприємство не буде продавати сировину, тому що при виробництві воно б одержало більший прибуток. У випадку ж f_max<φ_min покупець відмовиться від покупки сировини, тому що його плата за сировину більше прибутку від виробництва.

Результати вирішення двоїстої задачі виявляють найбільш дефіцитні види сировини (найбільш дефіцитним видом є та сировина, що в оптимальному рішенні двоїстої задачі має найбільшу ціну у_i). Аналіз рішення дозволяє визначити вплив збільшення запасів дефіцитної сировини на прибуток виробництва. Він може також підказати напрямок зміни технології виробництва, при якому дефіцитна сировина використовується в менших кількостях.

2. Поняття двоїстої задачі

Нехай є наступна задача лінійного програмування, її будемо називати прямою:

Задача 1.

Легко бачити, що до такого вигляду можна привести будь-яку ЗЛП. Двоїста задача для задачі 1 записуються так:

Задача 2.

Можна показати, що має місце принцип взаємної двоїстості: двоїстою до задачі 2 є задача 1. Таким чином, несуттєво, яку із задач 1 або 2 називати прямою, а яку двоїстою.

Приклад 1. Дана ЗЛП

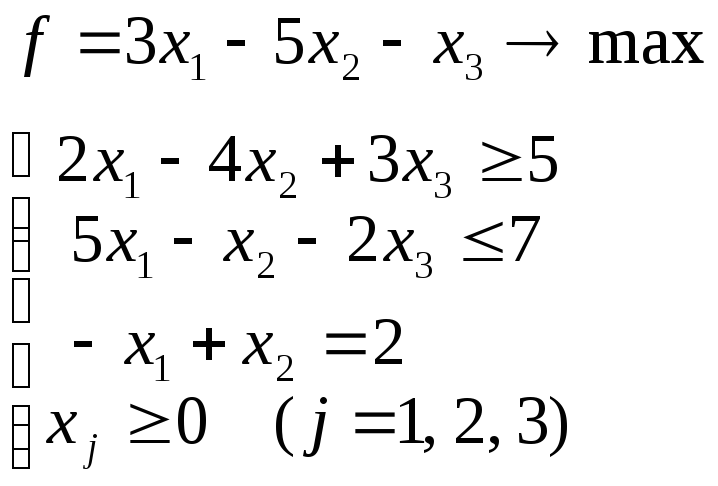
Побудувати двоїсту задачу.

Задачу потрібно привести до вигляду, в якому записана задача 1. Всі обмеження, крім вимог невід’ємності змінних, повинні бути нерівностями вигляду ≤. Першу нерівність помножимо на (-1). Потім замінимо рівність – x₁+x₂=2 двома нерівностями -x₁+x₂≤2 і -x₁+x₂≥2; другу із цих нерівностей помножимо на (-1). У результаті ЗЛП прийме вигляд:

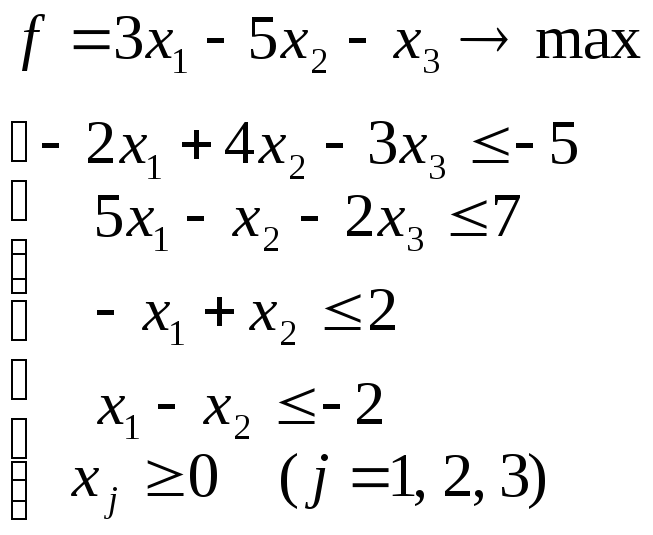
Тепер запишемо двоїсту задачу. Кожному лінійному обмеженню (крім вимог невід’ємності змінних) поставимо у відповідність змінну двоїстої задачі. Потім, рухаючись уздовж стовпців, запишемо цільову функцію й обмеження двоїстої задачі. Одержимо:

3. Теореми двоїстості

Приведемо без доказу наступні дві теореми.

Перша теорема двоїстості. Пряма задача розв'язна тоді й тільки тоді, коли розв'язна двоїста. При цьому f_max=φ_min.

Друга теорема двоїстості. Для того, щоб два припустимих рішення x₁', x₂',...,x_n' і у₁', у₂',…,y_m' пари двоїстих задач були оптимальними, необхідно й достатньо, щоб ці рішення задовольняли умовам

Друга теорема двоїстості дає можливість знаходити оптимальне рішення однієї з пари двоїстих задач, маючи оптимальне рішення іншої задачі.

Приклад 2. Дана задача

Побудувати двоїсту задачу, вирішити її геометрично, а потім за допомогою другої теореми двоїстості знайти оптимальне рішення прямої задачі.

Звернемо увагу, що дана задача записана у формі (4.4) - (4.6). Оскільки має місце принцип взаємної двоїстості, то будемо записувати двоїсту задачу у формі (4.1) - (4.3). Одержимо:

Вирішимо геометрично двоїсту задачу. Побудуємо на координатній площині граничні прямі (1) 8у₁–5у₂=11; (2) –у₁+3у₂=1; (3) –2у₁–7у₂=–7; знаходимо напівплощини, визначаємо ОПР, а потім знаходимо на ОПР оптимальну точку А (див. рисунок 4.1). Для відшукання координат точки А вирішуємо систему рівнянь

Одержуємо у₁=2, у₂=1. Підставивши ці значення змінних у цільову функцію, одержимо φ_max=7.

					Y2
									(5)
		(3)
						1				A
											•									(4)					Y1
						0,3			ОПР
				-1		0			1,4
													3,5
	(2)
							-2,2
	(1)

Рис. 4.1.

Для відшукання оптимального рішення вихідної задачі скористаємося другою теоремою двоїстості. Для цього запишемо систему рівностей (4.7) і (4.8)

Підставивши у₁=2, у₂=1, після очевидних перетворень одержимо систему

Вирішивши отриману систему, знайдемо х₁= 9/19; х₂=34/19; х₃=0; f_min= 7.

4. ТРАНСПОРТНА ЗАДАЧА

Симплекс-методом можна вирішити будь-яку ЗЛП. Але є такі ЗЛП, які можна вирішити простішими методами. До таких задач зараховані транспортні задачі. Прикладом транспортної задачі є задача про перевезення, задача про призначення, задача розвитку й розміщення одно- і багатопродуктових галузей.

1. Задача про перевезення.

Є m пунктів відправлення (ПВ) А₁, А₂,..., А_m, у яких зосереджений деякий вантаж у кількостях а₁,а₂,...,а_m і n пунктів призначення ( ПП.) В₁, В₂,..., В_n, у які потрібно завезти цей вантаж у кількостях b₁,b₂,...,b_n , причому

. Відомі вартості c_ij перевезення одиниці

вантажу з пунктів А_i у пункти В_j (;). Передбачається, що

а) товар є однорідним й діленим, тобто споживачеві байдужне джерело одержуваного товару, а перевезення можуть здійснюватися партіями будь-якого розміру;

б) вартість перевезення вантажу з одного пункту в інший пропорційна кількості перевезеного вантажу.

Потрібно скласти такий план перевезень із пунктів А_i у пункти В_j, при якому витрати на перевезення були б найменшими.

Вихідні дані задачі звичайно подаються у вигляді транспортної таблиці (табл. 5.1).

Таблиця 5.1

Пп Пв	В1	В2	. . .	В3	Запаси
А1	с11	С12	. . .	С1n	а1
А2	С21	С22	. . .	С2n	а2
. . .	. . .	. . .	. . .	. . .	. . .
Аm	Сm1	Сm2	. . .	Сmn	аm
Потреби	в1	в2	. . .	вn

Вартості c_ij проставляються в правих верхніх кутах відповідних клітинок.

Складемо математичну модель задачі. Нехай x_ij – кількість вантажу, перевезеного з пункту А_i у пункт В_j. Цільова функція задачі (загальна вартість перевезень) записується в такий спосіб:

Систему обмежень записуємо, керуючись тим, що:

а) запаси пунктів відправлення повинні бути вичерпані;

б) потреби пунктів призначення повинні бути задоволені;

в) перевезення можуть бути тільки невід’ємними.

Таким чином, обмеження задачі мають вигляд:

Ми бачимо, що задача про перевезення є ЗЛП.

2. Загальна постановка транспортної задачі

Транспортною задачею називається ЗЛП наступного вигляду:

Відзначимо наступну особливість транспортної задачі як ЗЛП спеціального вигляду: система рівнянь розбита на дві групи (5.2) і (5.3) так, що кожна змінна входить рівно в одне рівняння групи з коефіцієнтом 1.

Рівняння (5.2) називаються горизонтальними, рівняння (5.3) -вертикальними.

Будь-який набір значень змінних x_ij називається планом перевезень. План перевезень називається припустимим, оптимальним або опорним, якщо він є припустимим, оптимальним або опорним планом ЗЛП (5.1 - 5.4).

Транспортна задача, як і будь-яка задача лінійного програмування, може бути вирішена симплекс-методом. Однак завдяки зазначеній вище особливості транспортної задачі, для неї існують більш прості методи рішення, один із яких – метод потенціалів - ми вивчимо.

3. Відшукання початкового опорного плану перевезень

Існує декілька методів відшукування опорного плану транспортної задачі, серед них:

а) метод північно-західного кута;

б) метод мінімального елемента в рядку;

в) метод мінімального елемента.

Нехай є транспортна задача (5.1 - 5.4). Хоча в системі (5.2 - 5.3) m+n рівнянь, опорний план містить тільки m+n–1 базисних змінних. Це пояснюється тим, що одне з рівнянь є наслідком інших, і в жордановій формі m+ n–1 рівнянь.

Опишемо метод відшукання вихідного опорного плану, так званим методом північно-західного кута.

Візьмемо північно-західну клітинку (А_i,В_j). Проставимо в ній перевезення, що дорівнює min(a_i,b_j). Потім "зменшуємо" транспортну таблицю, керуючись правилами:

1. якщо a_i < b_j, то виключаємо з подальшого розгляду пункт відправлення (ПВ) А_i (і відповідний рядок); а в "меншій" таблиці потребу пункту призначення (ПП) В_j вважаємо рівною b_j - a_i ;

2. якщо b_j <a_i, то виключаємо ПП В_j (і відповідний стовпець); в "меншій" таблиці вважаємо запас ПВ А_i рівним a_i - b_j;

3. якщо a_i = b_j, то:

а) якщо в таблиці тільки один ПВ А_i і один ПП В_j, то алгоритм зупиняється;

б) якщо в таблиці один ПВ А_i і декілька ПП, то виключаємо В_j , вважаючи в "меншій" таблиці запас пункту А_i рівним 0;

в) якщо в таблиці один ПП В_j і декілька ПВ, то виключаємо А_i, вважаючи в "меншій" таблиці потребу пункту В_j, рівною 0;

г) якщо в таблиці декілька ПВ і декілька ПП, то виключаємо або ПВ А_i, вважаючи в "меншій" таблиці потребу ПП В_j рівною 0, або виключаємо ПП В_j, вважаючи запас ПВ А_i рівним 0.

Подібні кроки проробляють доти, поки не будуть виключені всі рядки й стовпці.

У результаті застосування методу північно-західного кута деякі клітинки заповнені, деякі - ні. Заповнені клітинки називаються базисними (навіть якщо стоїть 0), незаповнені - вільними. Доведемо, що число базисних клітинок дорівнює m+ n-1.

Дійсно, на кожному кроці, крім останнього, виключаємо або рядок, або стовпець. На останньому кроці виключаємо і рядок, і стовпець. Оскільки число рядків і стовпців у сумі дорівнює m+n, то всього буде пророблено m + n -1 кроків, а на кожному кроці заповнюється одна клітинка, відтак число базисних клітинок дорівнюватиме m + n -1.

Скористаємося прикладом (табл. 5.2).

Таблиця 5.2

ПП ПВ	В1	В2	В3	В4	Запаси
А1	10 4	15 3	5	7	25
А2	2	5 1	0 8	6	5
А3	0 4	9	30 3	15 2	45
Потреби	10	20	30	15	75=75

Розглянемо північно-західну клітинку транспортної таблиці - клітинку (1.1). Проставимо в ній перевезення x₁₁=min(a₁,b₁)=min(25,10)=10. Після цього потребу пункту В₁ повністю задоволено. Вилучаємо з таблиці перший стовпчик. В «меншій» транспортній таблиці запас пункту А₁ покладемо рівним 25 – 10 = 15. Розглянемо північно-західну клітинку нової «меншої» таблиці. Керуючись саме таким же правилом, проставимо в ній перевезення x₁₂= 15. Запас пункту А₁ вичерпаний, і ми вилучаємо перший рядок. В отриманій транспортній таблиці потреба пункту В₂ дорівнює 5. У північно-західну клітинку проставимо перевезення x₂₂=min(5,5)=5. При цьому одночасно вичерпано запас пункту А₂ і задоволено потребу пункту В₂ .Переходячи до нової таблиці, не можна одночасно вилучити і стовпець, і рядок – потребує вилучення або стовпець, або рядок. Виключимо з таблиці, наприклад, стовпець. Другій рядок ще не виключений з таблиці, тому запас пункту А₂ покладемо рівним 0, тому у північно-західну клітинку ставимо перевезення x₂₃=min(30,0)=0. Після цього виключаємо із розгляду другій рядок. Далі покладемо x₃₃=min(30,45)=30, виключаємо третій стовпець, проставляємо x₃₄=15 . Вихідний опорний план знайдено. Базисними змінними є х₁₁, х₁₂, х₂₂, х₂₃, х₃₃, х₃₄. Значення базисних змінних в опорному плані дорівнюють перевезенням, проставленим у відповідних клітках. Опорний план є вироджений, тому що х₂₃=0. Число базисних змінних дорівнює m+ n-1, тобто 3+4-1=6.

Метод північно-західного кута засвоюється дуже легко. Щоб переконатися в цьому, проробіть самостійно такий приклад (табл. 5.3.):

Таблиця 5.3

Пп Пв	В1	В2	В3	Запаси
А1	2	3	1	40
А2	4	2	5	60
А3	3	2	6	50
Потреби	70	40	40	150=150

У вас повинен вийти результат, зафіксований у таблиці 5.4.

Таблиця 5.4

Пп Пв	В1	В2	В3	Запасы
А1	2 40-	3	1 +	40
А2	4 30+ -	2 30- +	5	60
А3	3 +	2 -10+	6 - 40	50
Потребности	70	40	40	150 = 150