- •Министерство аграрной политики украины
- •Введение
- •Основы начертательной геометрии
- •Методы проецирования
- •Центральное проецирование
- •Параллельное проецирование
- •Проецирование точки на три плоскости проекций. Комплексный чертеж точки.
- •Тема: прямая. Положение прямой
- •Точка на прямой
- •Следы прямой
- •Взаимное положение прямых
- •1B 2a
- •Проецирование прямого угла
- •Определение натуральной величины отрезка прямой общего положения способом прямоугольного треугольника
- •Тема: плоскость
- •Положение плоскости относительно плоскостей проекций
- •3. Плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.
- •Пересечение прямой линии с плоскостью
- •Взаимное пересечение двух плоскостей
- •Расстояние от точки до прямой.
- •Расстояние от точки до плоскости. Построить плоскость, параллельную ∆авс и отстоящую от неё на n мм
- •Способы преобразования комплексного чертежа
- •Способ перемены плоскостей проекций
- •1.Определить нв прямой ав
- •2.Привести отрезок прямой общего положения в проецирующее положение
- •Сделать ∆ авс проецирующим
- •Вращение вокруг оси, параллельной плоскости проекций
- •Тема: геометрические тела Изображение многогранника на комплексном чертеже
- •Сечение многогранника проецирующей плоскостью Определение нв сечения
- •Пересечение многогранника с прямой
- •Тема: построение развёрток поверхностей
- •Развертка усеченной призмы
- •Развертка усеченного цилиндра
- •Развертка усеченной пирамиды
- •Развёртка усеченного конуса
- •Тема: аксонометрические Проекции
- •Прямоугольные проекции
- •2.Окружность в диметрии
- •Способ вспомогательных секущих плоскостей
- •Способ вспомогательных сфер
- •1. Определяем очевидные точки 12(11) и 22(21)
- •Тема : элементы технического рисования
- •© Кирсанова Валентина Викторовна
- •6.070104 «Морской и речной транспорт» специальности «Судовождение»,
- •6.050702 «Электромеханика»,
- •6.051701 «Пищевые технологии и инженерия»
Основы начертательной геометрии
Тема: ВВедение. методы проецирования.
проецирование точки на три
плоскости проекций.
Символы и обозначения, применяемые в начертательной геометрии
|
|
точки |
|
|
прямые и кривые линии |
|
|
горизонталь |
|
|
фронталь |
|
|
профильная прямая |
|
|
поверхности (плоскости) |
|
|
углы |
|
П1 ( Н ) |
горизонтальная плоскость проекций |
|
П2 ( V ) |
фронтальная плоскость проекций |
|
П3 ( W ) |
профильная плоскость проекций |
|
|
точка А принадлежит фигуре Ф |
|
|
точка А не принадлежит фигуре Ф |
|
|
фигура Фк - подмножество фигуры Ф |
|
|
фигура Фк - не есть подмножеством фигуры Ф |
|
|
фигуры Фк и Фi совпадают |
|
|
фигуры Фк и Фi не совпадают |
|
|
объединение фигур Фк и Фi |
|
|
пересечение фигур Фк и Фi |
|
|
параллельно |
|
|
не параллельно |
|
|
перпендикулярно |
|
|
скрещивание прямых |
|
◦ |
Изображение
точки, |
|
|
плоский или двугранный угол |
|
x,y,z |
оси проекций. Индексы при x, y и z обозначают соответствующие плоскости проекций. Например, ось x1 2 обозначает, что ось x разделяет поле горизонтальных проекций (индекс 1) и поле фронтальных проекций (индекс 2) |
Методы проецирования
Методы проецирования – это правила построения изображений, рассматриваемых в начертательной геометрии и применяемые в техническом черчении.
Изображение на плоскости предмета, расположенного в пространстве, полученное при помощи прямых линий – лучей, проведенных через каждую характерную точку предмета до пересечения этих лучей с плоскостью, называется проекцией этого предмета на данную плоскость.
Центральное проецирование
Задается плоскость проекций По и центр проецированияS, точка А, не лежащая в плоскости.
П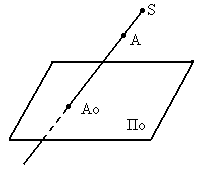 роведем
изSчерез А прямую до
пересечения с плоскостью По .
Получим центральную проекцию Ао точки А.
роведем
изSчерез А прямую до
пересечения с плоскостью По .
Получим центральную проекцию Ао точки А.
S– центр или полюс проецирования
По - плоскость проекций
SAо - проецирующий луч (проецирующая прямая)
Ао - центральная проекция точки А на плоскость
1 свойство: при заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну центральную проекцию.
Но если есть проекция точки, Sи П, то точку в пространстве найти нельзя.
2 свойство: каждая точка на плоскости проекций может быть проекцией бесконечного множества точек.

Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех её точек.
Центральные проекции линии не определяют проецируемую линию.
Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек.
ПРИМЕР: При построении на По проекции ∆ АВС достаточно построить проекции Ао, Во, Со трех его точек – вершин А, В и С.
Центральное проецирование применяют для изображения предметов в перспективе, но для технического черчения этот метод неудобен.