Способ вспомогательных секущих плоскостей

Суть способа – вспомогательная секущая плоскость одновременно пересекает поверхности каждого тела и образует фигуры сечения, контуры которых пересекаются. Точки пересечения контуров соединяют.

Этот способ применим тогда, когда контуры отдельных сечений представляют прямые линии или окружности.

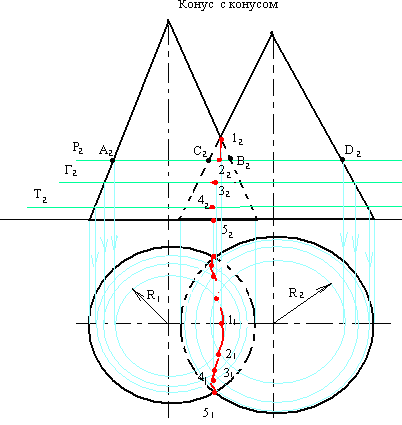
Точки 1 (1₂₎, 5 ( 5₁) и 5^/(5₁^/) являются очевидными – это точки пересечения очерковых и оснований конусов. Найдём соответствующие вторые проекции этих точек.

Проведём горизонтальную плоскость Р₂, которая рассечет оба конуса. В сечении конусов будут окружностиR₁= А₂В₂/2 иR₂ = С₂D₂/2 , причем их фронтальными проекциями являются прямые. Построим горизонтальные проекции этих сечений – окружности радиусомR₁иR₂.

На пересечении этих окружностей сечений на П₁определим горизонтальную проекцию общей точки – 2₁(2₁^/). Фронтальную проекцию точек 2 и 2^/определим по линиям связи на секущей плоскости Р₂.

Проведём еще ряд горизонтальных секущих плоскостей и определим проекции других промежуточных точек линии пересечения, которые соединим лекальной кривой с учётом видимости.

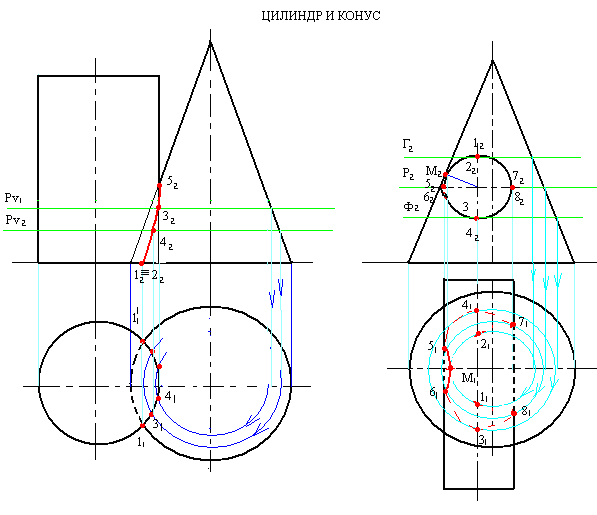
Рисунок 1

При взаимном пересечении конуса и цилиндра (рисунок 1) ось вращения цилиндра перпендикулярна П₂. Значит, на П₂линия пересечения совпадет с контуром основания цилиндра, т.е. фронтальной проекцией линии пересечения будет являться фронтальная проекция цилиндра.

Построив горизонтальную проекцию линии пересечения, на П₂на пересечении горизонтальной оси симметрии цилиндра с проекцией цилиндра наметим точки 5₂, 6₂, 7₂, 8₂– точки границы видимости линии пересечения, лежащие на экваторе цилиндра.

На П₁точки линии пересечения, лежащие выше экватора будут видимы, а точки, лежащие ниже экватора – невидимы.

Способ вспомогательных сфер

Этот метод можно применять при соблюдении следующих условий :

- пересекающиеся поверхности должны быть поверхностями вращения;

- их оси должны пересекаться ; точка пересечения осей является центром вспомогательных сфер;

- их оси должны быть // какой-либо плоскости проекций.

Сфера R_max проходит через самую дальнюю очевидную точку.

Сфера R_min должна касаться образующей большего тела, а меньшее тело – пересекать.

Сфера R_min определяется как большее расстояние от центра сфер до образующих обоих тел - перпендикуляры из центра сфер к очерковым образующим. Больший перпендикуляр и будет являться радиусом минимальной сферы.

Сфера пересекает тела по окружностям, проецирующимся на одну из плоскостей проекций отрезком.

1. Определяем очевидные точки 12(11) и 22(21)

2. Восстанавливаем перпендикуляры из центра сфер О₂к очерковым образующим цилиндра и конуса. Перпендикуляр к цилиндру О₂F₂ больше, чем перпендикуляр к образующей конуса. Значит, О₂F₂=Rи будет являться радиусом минимальной сферы. На П₂проводим из центра О₂этим радиусомRокружность, которая рассечет и конус и цилиндр по окружностям, фронтальной проекцией которых будут прямые – сечение конуса А₂В₂и сечение цилиндра С₂F₂.

На пересечении этих сечений определяем фронтальную проекцию точки 3 – 3₂.

3. На П₁строим горизонтальную проекцию сечения конуса, на котором находится точка 3 – окружность радиусом А₂В₂/ 2, на которой по линии связи определяем точки 3₁и 3₁^/.

1. Проводим ещё ряд секущих сфер радиусом больше минимальной и меньше максимальной и определяем другие промежуточные точки линии пересечения, которые соединяем лекальной кривой с учётом видимости.

Большее тело поглощает меньшее.

2. Видимость линии пересечения определяем следующим образом:

- на пересечении фронтальной проекции линии пересечения с осью симметрии цилиндра намечаем точку К₂(К₁и К₁^/определяем на П₁на очерковых образующих цилиндра);

- часть линии, находящаяся выше точки К – видимая. Точка К – граница видимости.

Вопросы для самопроверки

1. В чем заключается метод вспомогательных секущих плоскостей?

2. В чем заключается метод вспомогательных секущих сфер?

3. Как определить характерные точки?