Способы преобразования комплексного чертежа

Преобразование комплексного чертежа – это способы перехода от общих положений прямой и плоскости в системе П₁ и П₂ к частным в той же или дополнительной системе.

Существует два способа преобразования чертежа прямой линии или плоской фигуры общего положения в чертеж с их частным положением.

1.Заменяют заданную систему плоскостей проекций на новую так, чтобы относительно их исходные объекты оказались в частном положении, не меняя своего расположения в пространстве – способ перемены плоскостей проекций.

2.Изменяют положение исходных объектов в пространстве так, чтобы они приняли частное положение относительно плоскостей проекций – способ вращения.

Способ перемены плоскостей проекций

Заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система П₁П₂ дополняется плоскостями, образующими с П₁или П₂ между собой системы двух взаимно- перпендикулярных плоскостей, принимаемых за плоскости проекций.

Если задача дана на преобразование прямой, то её делают сначала прямой уровня, а затем – проецирующей.

Если задача на плоскость – плоскость сначала делается проецирующей, а затем – уровня.

1.Определить нв прямой ав

2.Привести отрезок прямой общего положения в проецирующее положение

1. Плоскость П₂ заменяем на новую плос кость П₄ перпендикулярную П₁ // АВ. Тогда новая ось П₁П₄ будет // А₁В_1.

Расстояние от оси П_{1 4} до А₄и В₄ равно соответственно расстоянию от А₂и В₂ до оси П_{1 2}. (т.е. расстояние до оси замеряем на той плоскости, которую заменяем).

2.Получили прямую в натуральную величину (сделали АВ прямой уровня). Заменяем П₁ на П₅, перпендикулярную П₄и перпендикулярную АВ. Тогда новая ось П₄П₅ будет перпендикулярна А₄В₄. От оси А₄В₄ по линиям связи, проведенным с П₄ на П₅ откладываем расстояния, равные расстояниям от А₁ и В₁ до оси П_{1 4}. АВ на П₅ спроецировалось в точку А₅ ≡В₅.

Сделать ∆ авс проецирующим

Вводим дополнительную плоскость, перпендикулярную плоскости треугольника АВС (надо ввести плоскость перпендикулярно любой прямой в плоскости треугольника – горизонтали или фронтали). От системы П₁/П₂переходим к системе П₁/П₄, где П₄ перпендикулярно П₁ и перпендикулярна ∆ АВС (проводим горизонтальh₂// оси Х и по линиям связи -h₁). Новая плоскость П₄перпендикулярнаh(ось П₁// П₄перпендикулярнаh₁и соответственно П₁).

Найти НВ плоской фигуры (∆ АВС)

Производим две замены.

Определить расстояние от точки А до прямой ВС

ВС делаем проецирующей. С₅ ≡ В₅А₅– расстояние искомое.

Определить расстояние между двумя параллельными прямыми

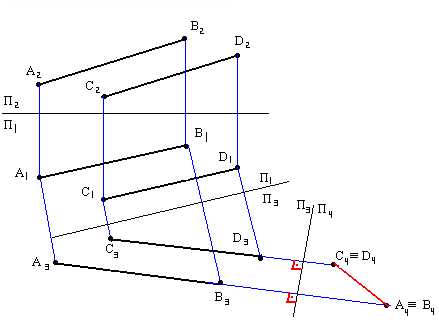
Прямые необходимо сделать проецирующими.

Определить расстояние между скрещивающимися прямыми

Способ вращения

Вращение вокруг проецирующей прямой

Через точку А проводим вертикальную осьi, вокруг которой поворачиваем отрезок до положения, параллельного фронтальной плоскости проекций – он займет положение А₁ // оси Х. На пересечении линии связи из с прямой, проведенной из В₂// оси Х получим . Отрезок А₂- есть НВ отрезка АВ.

Плоскопараллельное перемещение

Плоскопараллельным называется такое движение фигуры в пространстве, при котором все её точки перемещаются в плоскостях, // между собой и // одной из плоскостей проекций.

АВ перемещаем // П₂до положения, при котором отрезок станет // П₁–А₁¹В₁¹.

Для этого фронтальную проекцию А₂В₂не изменяя её величины располагают на свободном поле чертежа на П₂// оси Х. Из горизонтальной проекции А₁В проведем прямые,// оси Х до пересечения с вертикальными линиями связи из А₂^/В₂^/.

А₁^/В₁^/- НВ отрезка АВ.

Чтобы теперь сделать этот отрезок проецирующим, расположим А₁^/В₁^/перпендикулярно П₂. Из А₂^/В₂^/проведем прямые, параллельные оси Х до пересечения с линиями связи из А₁^// В₁^//.

АВ спроецировалась в точку А₂^{// ≡} В₂^//.

(Проекция фигуры на плоскости, относительно которой она перемещается, остается неизменной по своей величине и форме. А другие проекции точек этой фигуры перемещаются по прямым, параллельным оси Х ).

Найти НВ ∆ АВС и определить расстояние от точки S до ∆ АВС

1.Разворачиваем ∆ АВС в положение перпендикулярное П₂. Берм для этого горизонталь А1 и поворачиваем её перпендикулярно П₂на свободном поле чертежа на П₁. Тогда ∆ АВС, содержащий эту горизонталь, будет перпендикулярен П₂.

(Проекцию А₁1₁поворачиваем перпендикулярно оси Х и строим ∆ А^/₁В₁^/С₁^/методом засечек. Этим же методом строимS₁^/).

Проекции А₂ , В₂ , С₂ перемещаются по прямым // оси Х. На пересечении этих прямых с линиями связи из А₁^/ , В₁^/, С₁^/,S₁^/получаем точки А₂^/ , В₂^/, С₂^/,S₂^/.

∆АВС спроецировался в прямую А₂^/ В₂^/С₂^/.

2.Поворачиваем ∆ АВС //П₁(ось вращения проходит через В₂^/перпендикулярно П₂). Фронтальная проекция А₂^/ В₂^/С₂^/не изменяет вид и величину при повороте, т.е. поворачиваем А₂^/ В₂^/С₂^/// ОХ. При этом точки А^/₁ ,С₁^/перемещаются по прямым, // ОХ.

На пересечении этих прямых с линиями связи из А₂^//, С₂^//получаем точки А₁^//и В₁^//.

∆ А₁^//В₁^/С₁^//- НВ ∆ АВС.