
3й курс 6 семестр / S_mat
.pdf
|
|
|
x |
|
|
Py |
|
|
|
|
α |
|
y |
|
Pz |
y |
z |
P |
z |
z |
|||
|
A |
|
|
|
y |
x |
|
|
|
|
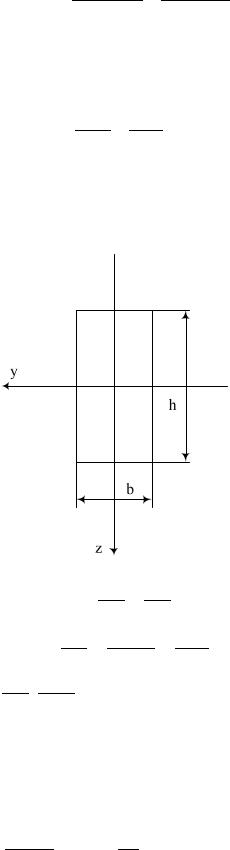
К концу консольной балки приложена сила «Р» не лежащая ни в одной из плоскостей симметрии, а наклонённая к оси «z» под углом α. Разложим эту силу на две составляющие:
= cos ,
= sin .
В данном случае каждая из двух составляющих силы Р будет производить изгиб балки относительно оси «Y» и «Z». Для расчёта балки на прочность необходимо определить опасное сечение и точку в этом сечении где напряжения будут наибольшими. Эта задача решается построением эпюр поперечных сил и изгибающих моментов. В случае косого изгиба таких эпюр будет две, для оси «Y» и для оси «Z».
Рассмотрим задачу определения точки балки где напряжения будут наибольшими. Для этого проведём сечение с координатой «Х» и определим напряжение в точке «А». Определим изгибающие моменты в проведённом сечении относительно оси «Y» и «Z»:
== cos ∙
== sin ∙
Для определения напряжения в точке «А» имеющей произвольные координаты «Y» и «Z» воспользуемся принципом независимости действия сил и определим это напряжение как алгебраическую сумму от действия двух изгибающих моментов My, и Mz.
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
< cos ∙ |
< sin ∙ |
|
cos |
|
sin |
|||
= − |
|
− |
|
= |
− |
|
= − |
+ |
|||||
|
|
|
|||||||||||
|
|
|
|
|
|
< = |
( ) |
|
|
|
|
||
Для определения точки в сечении где напряжения будут наибольшими необходимо знать положение центральной оси, то есть той оси на которой напряжения будут равны «0». Тогда
81

точка с наибольшими напряжениями в балке будет наиболее отдалённой от этой оси.
Определим положение этой оси. Точку в сечении удовлетворяющую этому условию обозначим
«yo, zo».
0 = − |
cos |
+ |
sin |
Из этого уравнения следует, что выражение в скобках равно нулю. То есть:
cos |
+ |
sin |
= 0 |
Полученное уравнение представляет собой уравнение нейтральной оси, так как обе координаты входят в уравнение в первой степени, то данная ось – прямая. Выразим это уравнение в более удобном виде:
cos |
|
= − |
sin |
|
= − |
|
|
tan |
∙ |
|
|
|||
Изобразим положение нейтральной оси в сечении балки согласно полученного уравнения.
y
z 
Для определения точек наиболее удалённых от нейтральной оси проведём две касательных к контуру сечения и параллельных нейтральной оси. Точки касательных и будут наиболее отдалёнными точками сечения от нейтральной оси. Для сечения имеющего выступающие углы (двутавровое, квадратное, прямоугольное), точки наиболее удалённые от нейтральной оси при любом его положении будут точками наиболее удалёнными от координатных осей «y, z». Таким образом определив положение точек наиболее удалённых от нейтральной оси мы можем определить наибольшее напряжение в этих точках.
82
Подставим значение этих точек в уравнение для напряжений можем записать для опасного сечения балки условие прочности:
| | = | | |
cos |
+ |
sin |
≤ [ ] |
В данном уравнении:
|
|
|
= |
; |
|
|
|
|
= |
|
|
|
|
|
|
||||
| |
| |
cos |
+ |
sin |
|
≤ [ ] |
|||
Для решения задачи на прочность для прямоугольного сечения определяются оба момента сопротивления через один из параметров сечения. Тогда условие прочности будет иметь одну неизвестную.
|
|
|
|
= |
|
|
= |
|
|
|
|
||
|
|
|
|
6 |
|
|
6 |
|
|||||
= |
|
|
= |
|
( ) |
|
= |
|
|||||
|
6 |
|
|
6 |
|
|
6 |
||||||
6 |
cos |
+ sin |
| |
|
|
| ≤ [ ] |
|||||||
В случае если требуемое сечение является двутавром, то задача подбора сечения из условия прочности решается методом последовательных приближений, так как для этого сечения не существует аналитической зависимости между главными моментами сопротивления сечению. Рассмотрим решение следующей задачи.
| | cos + sin ≤ [ ]
83

Для двутаврового сечения из справочника по прокатным профилям выбирается наименьшее сечение и определяется отношение моментов сопротивления.
Минимальное:
=
Наибольшее:
=
Определяется среднее значение из двух полученных:
ср = |
|
+ |
|
|
2 |
|
Полученное значение подставляется в условие прочности, из справочника выбираются оба момента сопротивления и определяется отношение:
|
|
= |
Определяется среднее отношение: |
||
ср = |
ср + |
|
2 |
||
Полученное отношение подставляется в условие прочности и цикл повторяется. Подбор сечения считается законченным если максимальное напряжение в сечении не превосходит допускаемое либо превышает его не более чем на 5%.
26. ВНЕЦЕНТРЕННОЕ СЖАТИЕ.
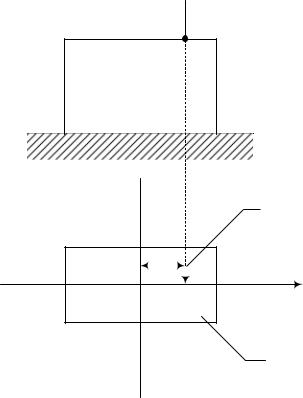
Если сжимающая (растягивающая) сила приложена в точке отстоящей от центра тяжести сечения и имеющей произвольные координаты, то такое состояние называется внецентренным сжатием. Рассмотрим случай внецентренного сжатия.
84
 P
P
y 
A
xp

 yp x
yp x
F
Пусть к стержню имеющему площадь F приложена сила Р в точка А имеющей координаты «хр», и «yp». Для расчёта на прочность в этом случае не требуется определять опасное сечение, так как во всех сечениях будут действовать одни и те же силовые факторы.
Определим их. Так как точка приложения силы смещена по отношению к координатным осям то кроме растяжения эта сила будет создавать и изгибающий момент по отношению к координатным осям.
=
=
Определим напряжение в произвольной точке «М» имеющей координаты (x, y)
используя принцип независимости действия сил. Напряжение в точке М будет являться алгебраической суммой от трёх силовых факторов.
|
|
|
|
|
< |
< |
|||||
= |
|
+ |
|
+ |
|
= |
|
+ |
|
+ |
|
|
|
|
|
|
|
||||||
Для определения точки в сечении где напряжения будут наибольшими необходимо определить положение нейтральной оси. Наиболее удалённые от оси точки и будут иметь наибольшее напряжение. Полученное уравнение определяет напряжение в любой точке стержня. С его помощью можно определить положение нейтральной оси. Для этого обозначим координаты точки лежащей на этой оси как «хо, и уо» и подставим в полученное уравнение.
Кроме этого напряжения на нейтральной оси будут равны нулю, тогда:
85
|
|
|
∙ |
|
0 = |
|
1 + |
|
+ |
|
|
|||
В получено уравнении выражение:
≠ 0
Следовательно:
1 + |
∙ |
= 0 |
+ |
В полученном уравнении:
= ; =
ix – радиус инерции. Тогда:
1 + |
|
+ |
|
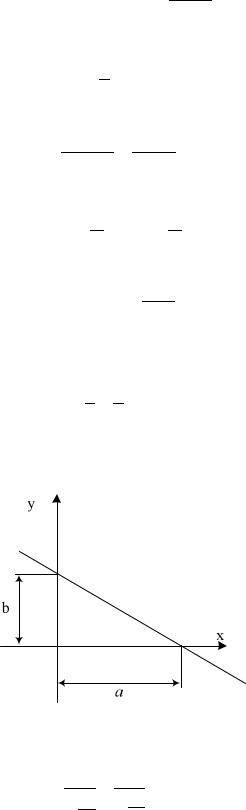
Подставим уравнение нейтральной оси в более удобном виде. В виде уравнения прямой в отрезках на осях.
+= 1
где: a и b – отрезки, которые отсекает прямая, по отношению к осям Х и Y
соответственно.
− |
|
− |
|
= 1 |
|
|
+= 1
−−
Изобразим положение нейтральной оси в сечении стержня.
86

Для определения точки сечения, где напряжения будут наибольшими проведём касательные к контуру сечения и параллельные нейтральной оси. Определим напряжения в точках 1 и 2.
=+ +
Определим напряжения в центре тяжести сечения стержня. Для этого подставим в уравнение определяющее напряжения в точке М координаты х и у.
=
Определив наибольшие напряжения в сечении стержня можно записать условие прочности. Для сечения имеющего выступающие углы (прямоугольное, двутавровое,
квадратное) точки наиболее удалённые от нейтральной оси совпадают с точками наиболее удалёнными от координатных осей «Х, Y». Поэтому для таких сечений условие прочности примет вид:
= |
|
+ |
|
+ |
|
|
Где:
|
= , |
|
= |
|
|
С учётом этого условие прочности имеет вид:
= + + ≤ [ ]
Задача подбора сечения в случае внецентренного сжатия решается методом последовательных приближений.
87

Понятие о ядре сечения.
Если в качестве материала для стержня анизотропный материал, то целесообразно,
чтобы напряжения во всех точках сечения были одинакового знака. Эта задача решается определением некоторой области сечения, называемой ядром сечения. Приложение сил в эту область позволяет получить напряжения во всех точках сечения с одинаковым знаком.
Для определения ядра сечения воспользуемся уравнением нейтральной оси, но при этом для получения ядра сечения задача будет обратной. То есть определяются координаты точки приложения сил находящиеся на контуре ядра сечения. При этом нейтральная ось в предельном положении должна касаться контура сечения стержня. Поэтому для определения координат точек ядра сечения обкатаем касательную к контуру сечения и получим геометрическое место точек сечения.
− |
|
− |
|
= 1 |
|
|
Для определения уравнения ядра сечения заменим координаты «Xp, Yp» на координаты сечения «Xя, Yя». То есть на координаты точек ядра сечения.
−я − я = 1
Подставим значение точек касательных «X0, Y0» и определим координаты ядра. Задача определения ядра сечения решается для прямоугольных контуров определение 4–х точек контура ядра сечения которые соединяются прямыми отрезками.
88

27. ИЗГИБ С КРУЧЕНИЕМ.
Этот вид сложно напряженного состояния наблюдается в валах зубчатых редукторов,
цепных и ременных передач. Поэтому расчёт этих элементов необходимо вести на кручение с изгибом. Рассмотрим пример последовательности расчёта вала на изгиб с кручением.
1.Спроецируем все силы, действующие на данный вал на соответствующие плоскости.
2.Составим уравнения равновесия и определим реакции опор. Определив опорные реакции, строим эпюры изгибающих моментов в двух плоскостях – ZY и XY.
3.Для определения опасного сечения строим эпюру суммарного изгибающего момента определяемого по формуле:
M из 
 M 2y M 2x
M 2y M 2x
4.Строим эпюру крутящего момента. В рассматриваемом примере крутящие моменты будут в промежутке между крутящими колёсами.
5.Определяем опасное сечение вала которое будет иметь максимальный суммарный изгибающий момент и максимальный крутящий момент.
27.1.РАСЧЁТ НА ПРОЧНОСТЬ ВАЛА РАБОТАЮЩЕГО НА КРУЧЕНИЕ С ИЗГИБОМ.
После построения эпюр изгибающих моментов и крутящего момента действующих в сечении вала, приступают к определению опасного сечения. Иногда их может быть несколько, в
этом случае определяется эквивалентный изгибающий момент для всех подозрительных сечений и выбирается наибольший. Задача определения точки сечения, где напряжения будут максимальными, не представляет особого труда, так как сечение вала круглое. Поэтому при косом изгибе, при любом положении нейтральной оси (то есть оси, которая проходит через центры тяжести сечений) точки наиболее отдалённые от этой оси будут находиться на максимальном расстоянии равном “R”.
Для случая сложного напряжённого состояния, которым является кручение с изгибом необходимо определить сочетание наибольших нормальных и касательных напряжений.
Благодаря тому, что наибольшие касательные напряжения находятся на поверхности вала, эта задача упрощается, так как всегда существует две точки сечения, где и нормальные и касательные напряжения будут наибольшими.
Таким образом, в сечении вала работающего на кручение с изгибом всегда будет иметь место сочетание двух наибольших напряжений, нормального от изгиба и касательного от кручения. Поэтому при рассмотрении расчёта на прочность для этого случая рассмотрим все четыре теории прочности. Все эти теории используют главные напряжения для расчёта на прочность. Определим эти напряжения.
89

Максимальное нормальное напряжение от действия максимального суммарного момента:
| |
=
Максимальное касательное напряжение от действия кручения:
кр
=
где:
=2 = 0,1
=16 = 0,2
Отсюда можно записать, что:
кр
= 2$
Зная главные напряжения, перейдём к рассмотрению теорий прочности.
ПЕРВАЯ ТЕОРИЯ ПРОЧНОСТИ (теория прочности наибольших нормальных напряжений)
Согласно этой теории следует, что прочность материала находящегося в сложном напряжённом состоянии будет обеспечена, если наибольшее нормальное напряжение для этого случая не превосходит допустимого нормального напряжения для одноосного напряжённого состояния.
Определим наибольшие напряжения для такого случая. Эта задача связана с определением главных напряжений. Согласно ранее полученным формулам главное напряжение:
|
= |
− |
± |
1 |
|
− |
+ 4Z |
|
2 |
2 |
|
Для нашего случая максимальное напряжение будет равно:
= |
2 + |
1 |
+ 4Z |
2 |
Подставим в это выражение значение полученных величин “σ” и “τ”.
|
|
|
1 |
|
|
|
|
|
кр |
1 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
= |
2$ |
+ |
2 |
|
|
|
+ 4 |
4Z |
= |
|
2 |
+ |
2 |
|
+ кр |
||
|
|
|
|||||||||||||||
|
|
|
|
= |
|
1 |
|
+ |
|
|
+ кр |
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
90
