
- •Высшая математика конспект лекций
- •1 Курс, 1 семестр
- •Содержание
- •Тема 1 «Элементы линейной алгебры» 7
- •Тема 2 «Элементы векторной алгебры» 22
- •Тема 3 «Элементы аналитической геометрии» 30
- •Тема 4 «Введение в анализ» 51
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» 66
- •Введение
- •Тематический план
- •§ 2. Определители 3-го порядка
- •§ 3. Миноры и алгебраические дополнения
- •§ 1. Определители высших порядков.
- •Система двух уравнений с двумя неизвестными
- •Система 3-х уравнений первой степени с 3-мя неизвестными
- •Понятие о матрицах
- •Сложение матриц и умножение их на число
- •Транспонирование матриц
- •Перемножение матриц
- •Решение систем линейных уравнений методом Гаусса
- •Решение систем 3-х уравнений с 3-мя неизвестными с помощью формул Крамера
- •Исследование систем линейных уравнений
- •§ 1. Общие понятия. Систему уравнений вида
- •§ 2. Система 2-х уравнений с 2-мя неизвестными
- •§ 3. Система 3-х уравнений с 3-мя неизвестными
- •Вопросы для самоконтроля
- •Тема 2 «Элементы векторной алгебры» Основные понятия
- •Линейные операции над векторами
- •Линейная зависимость и независимость векторов
- •Определение координат вектора в данном базисе
- •Системы координат и скалярное произведение векторов Декартова система координат
- •Полярная система координат
- •Скалярное произведение векторов.
- •Векторно-скалярное (смешанное) произведение
- •§ 1. Вычисление объема параллелепипеда
- •§3.Направляющие косинусы
- •Вопросы для самоконтроля
- •Тема 3 «Элементы аналитической геометрии»
- •П 4. Переход от полярных координат к декартовым и обратно
- •Простейшие задачи аналитической геометрии на плоскости п 1. Проекция отрезка на оси координат
- •П 2 .Расстояние между двумя точками на координатной плоскости
- •П 3. Деление отрезка в данном отношении
- •Линии и их уравнения п 1. Понятие уравнения линии
- •П 2. Примеры заданий линий при помощи уравнений
- •П 3. Получение линии как геометрического места точек
- •П 4. Параметрические уравнения линий
- •П 5. Алгебраические линии
- •Прямая на плоскости п 1. Угловой коэффициент
- •П 3. Уравнение прямой, проходящей через данную точку м1 (х1; у1)
- •П 8. Уравнение прямой в отрезках
- •П 9. Нормальное уравнение прямой
- •П. 10. Расстояние от точки до прямой
- •П. 11. Уравнение прямой в полярных координатах
- •П. 3 Эллипс и его каноническое уравнение
- •П.4 Эксцентриситет и директрисы эллипса
- •Гипербола и ее каноническое уравнение
- •П 6. Асимптоты гиперболы
- •П 7. Эксцентриситет и директрисы гиперболы
- •П. 8 Парабола и ее уравнение
- •П. 9 Уравнение эллипса, гиперболы и параболы в полярных координатах
- •Преобразование координат п. 1 Преобразование координат при параллельном сдвиге осей
- •П 3. Преобразование декартовых координат при изменении начала и поворота осей
- •П. 4 Преобразование общего уравнения второй степени не содержащего произведения переменных
- •П 5. Преобразование общего уравнения второго порядка
- •Аналитическая геометрия в пространстве Уравнение прямой
- •Понятие об уравнении плоскости.
- •Уравнения поверхностей
- •Вопросы для самоконтроля
- •Тема 4 «Введение в анализ» Переменные и постоянные величины. Понятие функции.
- •Основные характеристики функций.
- •Основные элементарные функции и их графики.
- •Числовая последовательность.
- •Предел функции.
- •Бесконечно малые величины.
- •Бесконечно большие функции.
- •Соотношение между бесконечно малыми и бесконечно большими функциями.
- •Основные теоремы о пределах.
- •Типы неопределенностей и способы их раскрытия.
- •Первый замечательный предел.
- •Эквивалентные бесконечно малые и основные теоремы о них.
- •Непрерывность функций.
- •Основные теоремы о непрерывных функциях.
- •Вопросы для самоконтроля
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» Определение производной.
- •Геометрический смысл производной.
- •Производные основных элементарных функций.
- •Производная сложной и обратной функции.
- •Дифференцирование неявно заданной функции.
- •Дифференцирование функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Производные высших порядков.
- •Производные высших порядков неявно заданной функции.
- •Производные высших порядков от функций заданных параметрически.
- •Дифференциал функции.
- •Правила вычисления дифференциала.
- •Приложения производной.
- •Исследование функций при помощи производной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Вопросы для самоконтроля
- •Литература
Тема 2 «Элементы векторной алгебры» Основные понятия
Вектором
называется направленный отрезок
![]() .
Обозначается
.
Обозначается
![]() или
или
![]() .
Вектор характеризуется длиной (модулем)
.
Вектор характеризуется длиной (модулем)
![]() или
или
![]() и направлением. Нулевой вектор
и направлением. Нулевой вектор
![]() .
.
Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются компланарными, если существует плоскость, которой они параллельны. Т.е. они лежат на одной или параллельных плоскостях.
Два вектора называются равными, если они коллинеарные, одинаково направлены и имеют равные длины. Векторы бывают свободными, скользящими и приложенными.
Линейные операции над векторами
Сложение векторов и умножение их на число называют линейными операциями.
![]()
![]() .
При этом вектор
.
При этом вектор
![]() коллинеарен вектору
коллинеарен вектору
![]() .
.
![]() .
Векторы
.
Векторы
![]() и
и
![]() направлены одинаково, если
направлены одинаково, если
![]() и противоположно, если
и противоположно, если
![]() (если
(если
![]() ,
то
,
то
![]() есть нулевой вектор).
есть нулевой вектор).
Сложение векторов коммутативно (переместительно)
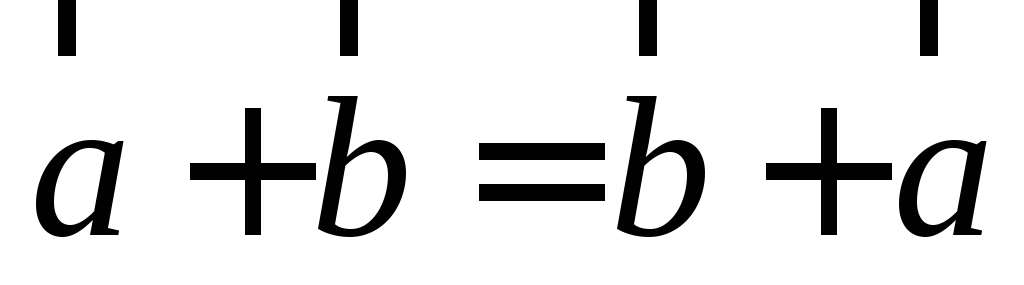 .
.Сложение векторов ассоциативно (сочетательно)
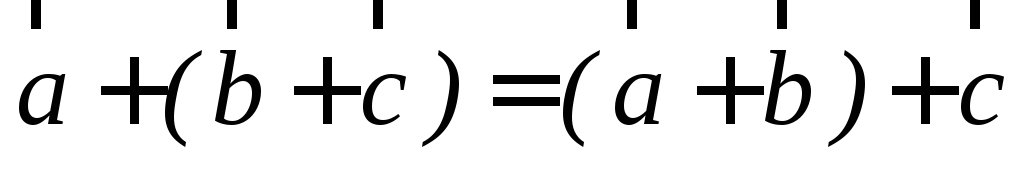 .
.Любой вектор
 не изменится, если к нему добавить
нулевой вектор
не изменится, если к нему добавить
нулевой вектор
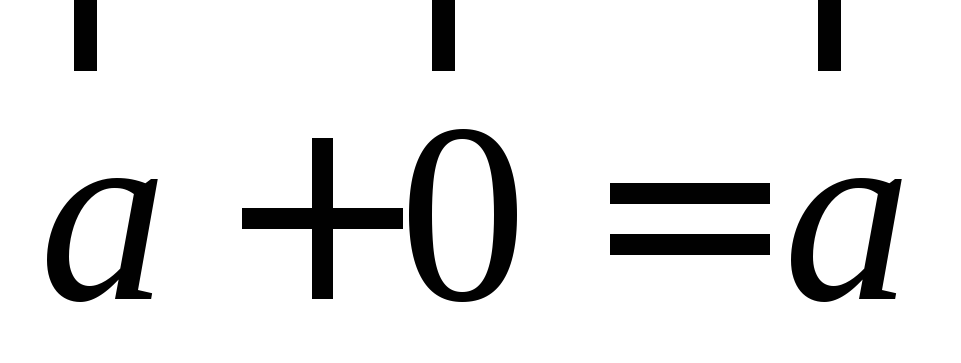
Векторы
 и
и
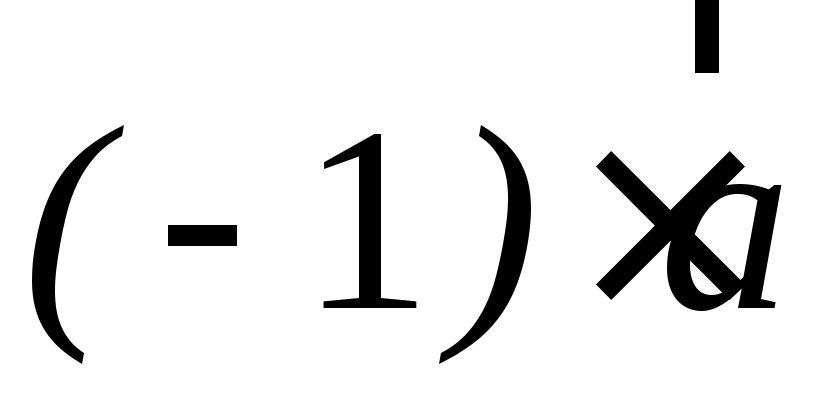 являются противоположными, т.е.
являются противоположными, т.е.
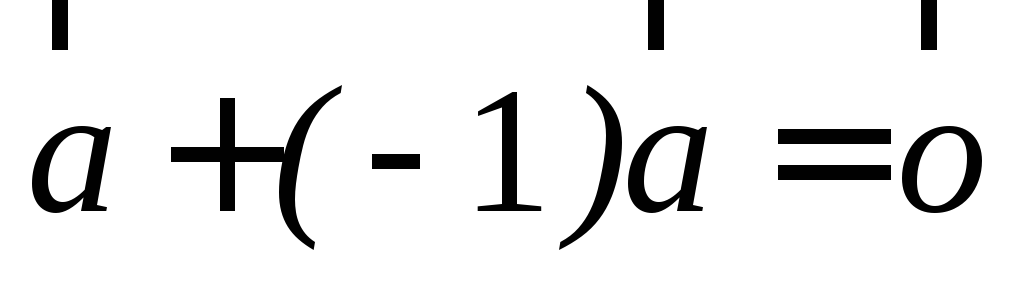 .
.Умножение вектора на число ассоциативно, т.е. для любых чисел α и β будет
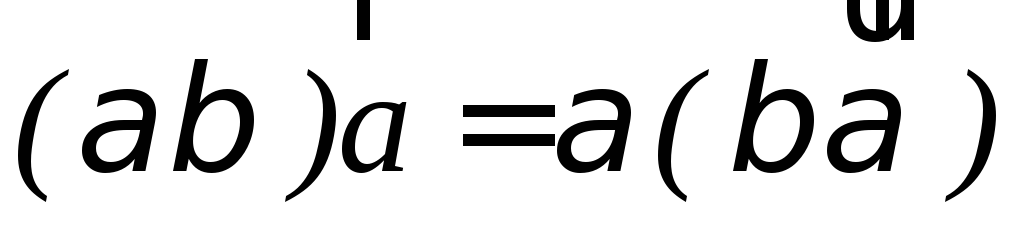 .
.Умножение вектора на число дистрибутивно (распределительно) т.е.
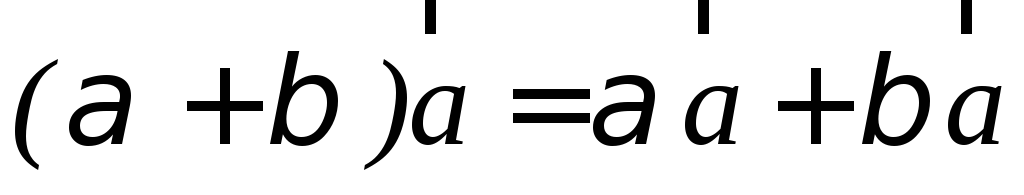 .
.Если мы имеем два вектора, то
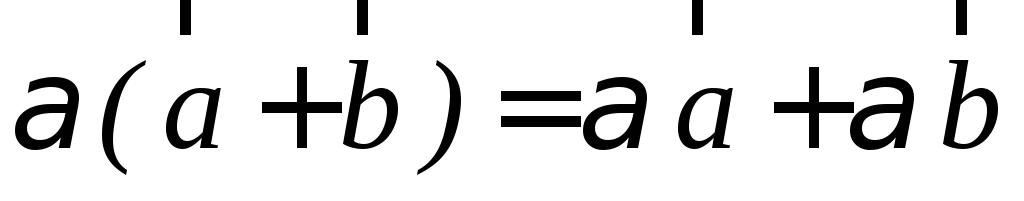 .
.Умножение вектора на 1 его не изменяет
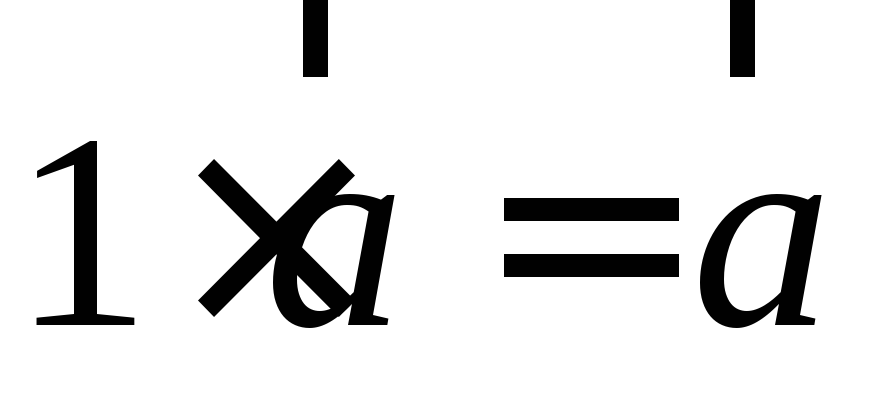 .
.
В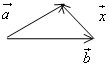 ектор,
противоположный вектору
ектор,
противоположный вектору
![]() обозначается
обозначается
![]() .
.
![]() .
Вычитание
.
Вычитание
![]() можно представить
можно представить
![]() или
или
![]()
Если
нам надо разделить вектор
![]() на α,
то мы его множим на
на α,
то мы его множим на
![]() .
.
Применяя
линейные операции (сложение, умножение)
мы можем составлять суммы векторов,
умноженных на числа:
![]() .
.
Выражения такого вида называются линейными комбинациями векторов.
Числа α1, α2,….αn называются коэффициентами.
Линейные
комбинации обладают такими очевидными
свойствами: если векторы
![]() коллинеарны, то любая их линейная
комбинация им коллинеарна (т.к. вектора
остаются параллельными).
коллинеарны, то любая их линейная
комбинация им коллинеарна (т.к. вектора
остаются параллельными).
Если
векторы
![]() компланарны, то любая их линейная
комбинация с ними компланарна.
компланарны, то любая их линейная
комбинация с ними компланарна.
Линейная зависимость и независимость векторов
Пусть
мы имеем векторы
![]() .
Если один из этих векторов может быть
представлен в виде линейной комбинации
остальных векторов, то эти векторы
называются линейно- зависимыми , т.е.
.
Если один из этих векторов может быть
представлен в виде линейной комбинации
остальных векторов, то эти векторы
называются линейно- зависимыми , т.е.
![]() .
А если два линейно-зависимых вектора,
то
.
А если два линейно-зависимых вектора,
то
![]() или
или
![]() .
.
Векторы
![]() называются линейно-независимыми, если
их линейная комбинация
называются линейно-независимыми, если
их линейная комбинация
![]() только при
только при
![]() .
Для линейно-независимых векторов нельзя
представить один из них в виде линейной
комбинации других, т.е.
.
Для линейно-независимых векторов нельзя
представить один из них в виде линейной
комбинации других, т.е.
![]()
Система n линейно независимых векторов в n-мерном пространстве
называется базисом этого пространства. Если на плоскости (в 2-мерном пространстве) базисом будут два (не коллинеарных) вектора, то в пространстве базисом будут 3 некомпланарных вектора и.т.д.
Пусть
в общем случае векторы
![]() и образуют базис n-мерного
линейного пространства (т.е. имеет n
линейно независимых векторов). Если мы
добавим вектор
и образуют базис n-мерного
линейного пространства (т.е. имеет n
линейно независимых векторов). Если мы
добавим вектор
![]() в этом же пространстве, то получим
линейно зависимую систему, т.е.
в этом же пространстве, то получим
линейно зависимую систему, т.е.
![]() (1)
(1)
Причем
некоторые из них отличны от нуля и
обязательно
![]() ,
в противном случае бы
,
в противном случае бы
![]() и
и
![]() ,
что противоречит определению линейной
независимой системы. Поэтому
,
что противоречит определению линейной
независимой системы. Поэтому
![]() .
Т.е.
.
Т.е.
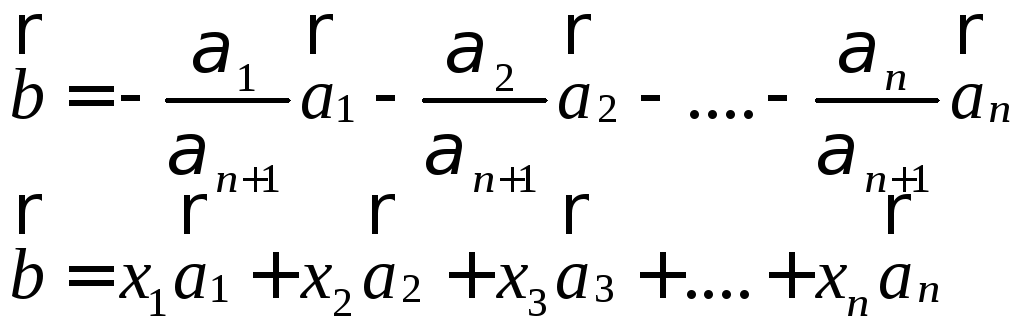 (2)
(2)
