Основные характеристики функций.

Опр. Функция , определенная на множестве называется четной, если для любого выполняется условие и ; нечетной, если для любого выполняется условие и .

График четной функции симметричен относительно оси Оy, нечетной – относительно начала координат.

Например: - четные функции; а - нечетные функции; - функции общего вида, т.е. не четные и не нечетные.

Опр. Пусть функция определена в промежутке . Если для любой пары значений , из неравенства следует неравенство, функция называется возрастающей на данном промежутке, если – функция называется неубывающей.

Иными словами – значения возрастающей функции увеличиваются одновременно со значением аргумента.

Опр. Если для любых и из промежутка вытекает , то функция называется убывающей в интервале , если - невозрастающей.

Например, функция, заданная графиком (рис.1), убывает на интервале (-2;1), не убывает на интервале (1; 5), возрастает на интервале (3; 5).

Опр. Возрастающие, невозрастающие, убывающие и неубывающие называются монотонными, а возрастающие и убывающие – строго монотонными. На рисунке (рис.1) функция строго монотонна на (-2;1) и (3; 5); монотонна на (1; 3).

Опр. Функция , определенная на множестве D, называется ограниченной, если существует такое число М>0. что для всех выполняется неравенство .

График ограниченной функции лежит между прямыми и (рис.2).

Опр. Функция называется периодической на множестве D, если существует такое число Т>0, что при каждом значении и . При этом число Т называется периодом функции.

Опр. Пусть задана функция с областью определения D и множеством значений Е. Если каждому значению соответствует единственное значение , то определена функция с областью определения Е и множеством значений D. Такая функция называется обратной к функции и записывается .

Функции и являются взаимно обратными. Чтобы найти функциюобратную к функции достаточно решить уравнение относительно х (если это возможно).

Пример:

1. Для функции 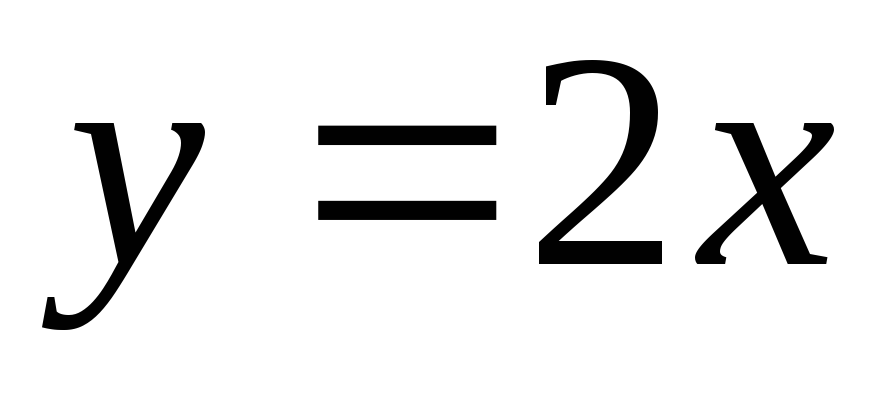обратной является функция ;

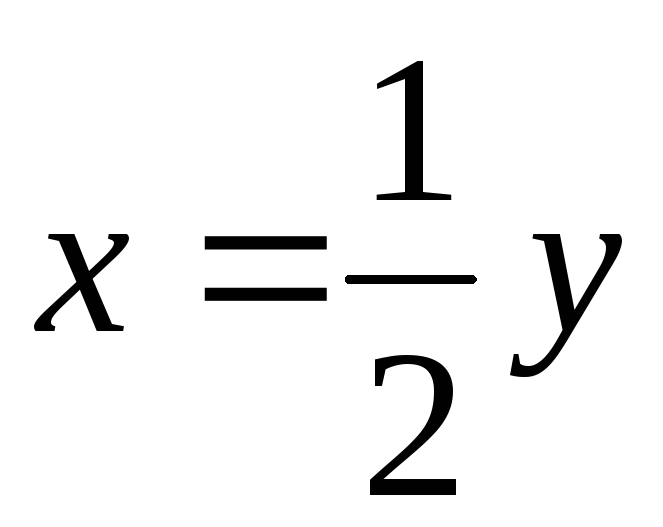2. Для функции 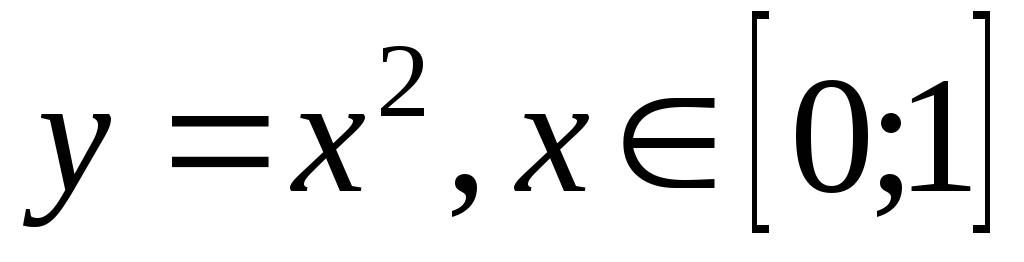, обратной функцией является .

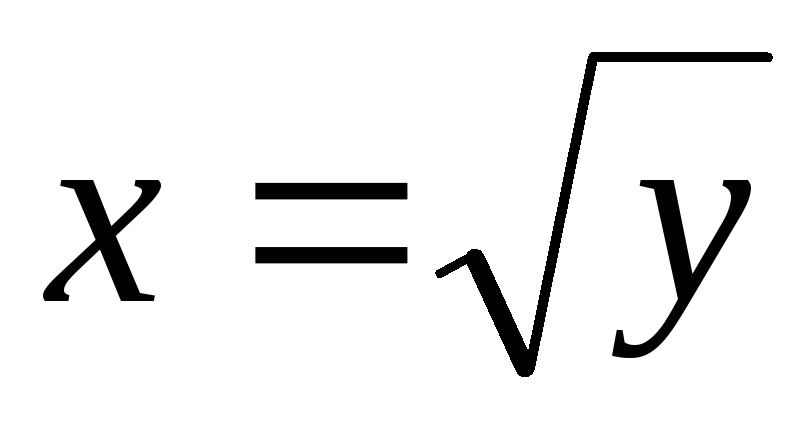З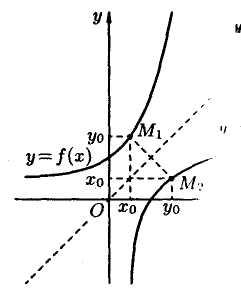амечание: Любая строго монотонная функция имеет обратную. При этом, если функция возрастает (убывает), то обратная тоже возрастает (убывает). Если функцииy=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графиком их является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.

Опр. Пусть функция определена на множестве D, а функция на множестве , причем для соответствующее значение . Тогда на множестве определена функция , которая называется сложной функцией от х (или функцией от функции). Переменную называют промежуточным аргументом сложной функции.

Например, Функия есть сложная функция с промежуточным аргументом . Сложная функция может иметь несколько промежуточных аргументов.