§ 2. Определители 3-го порядка

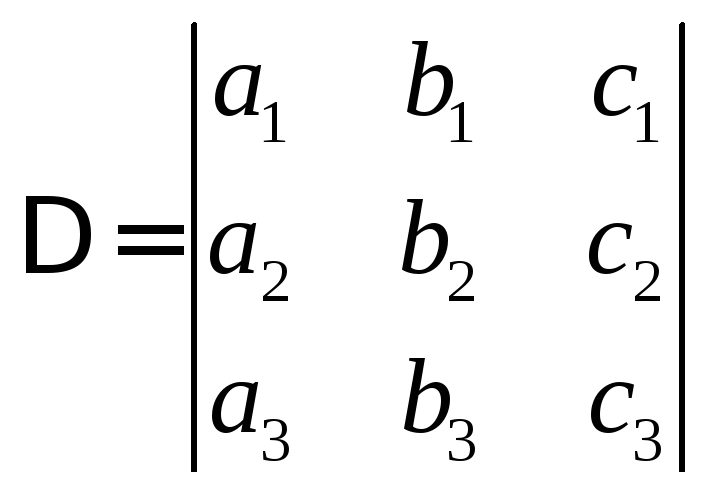Он имеет 9 элементов. При этом у него 3 строки и 3 столбца. Вычисляется он следующим образом

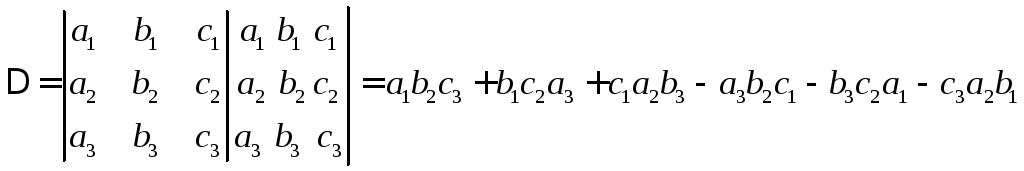
Например

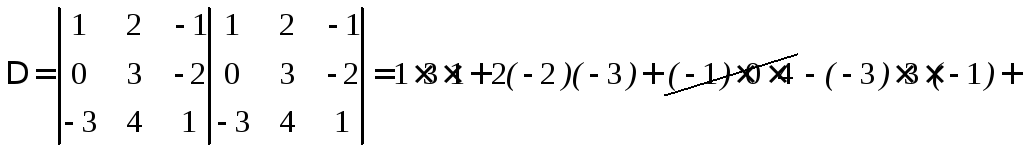
Т.к. последний столбец лишний, то его не дописывают

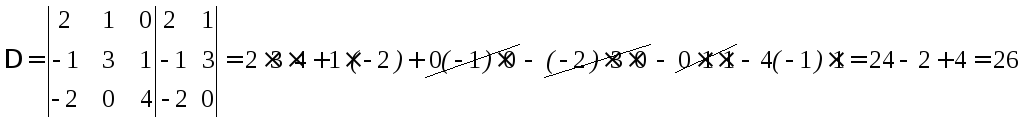
Все свойства определителей 2-го порядка относятся и к определителям 3-го порядка.

Например

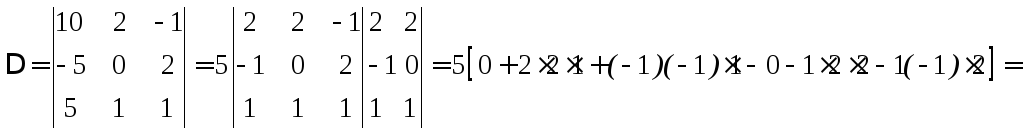
. Или

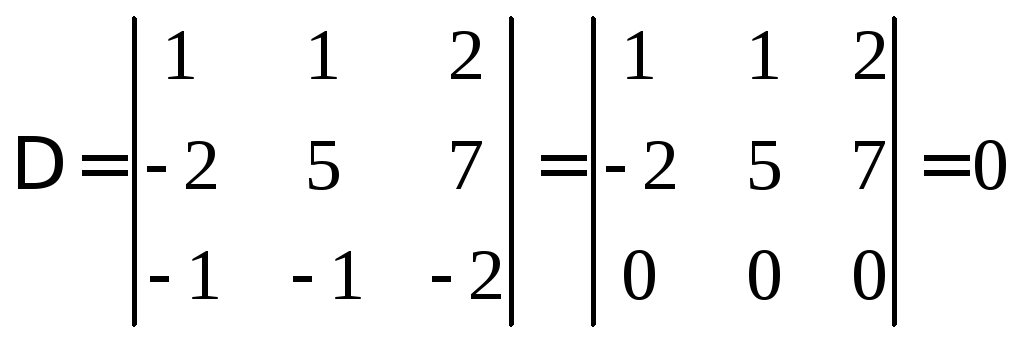
§ 3. Миноры и алгебраические дополнения

Минором, соответствующим данному элементу определителя третьего порядка называется определитель 2-го порядка, полученный из данного вычеркиванием строки столбца, на пересечении которого стоит данный элемент.

Например

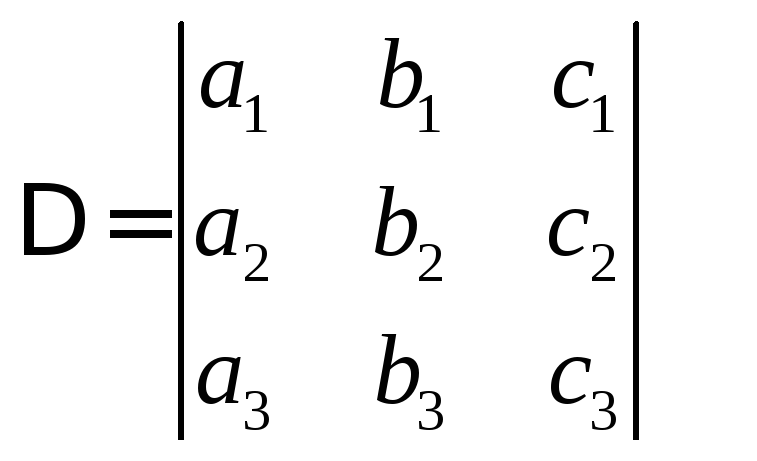
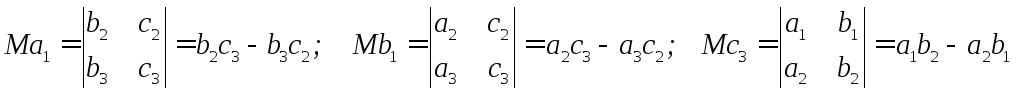и.т.д.

В дальнейшем мы будем рассматривать определители 4, 5 и высших порядков. Поэтому для удобства обозначаем

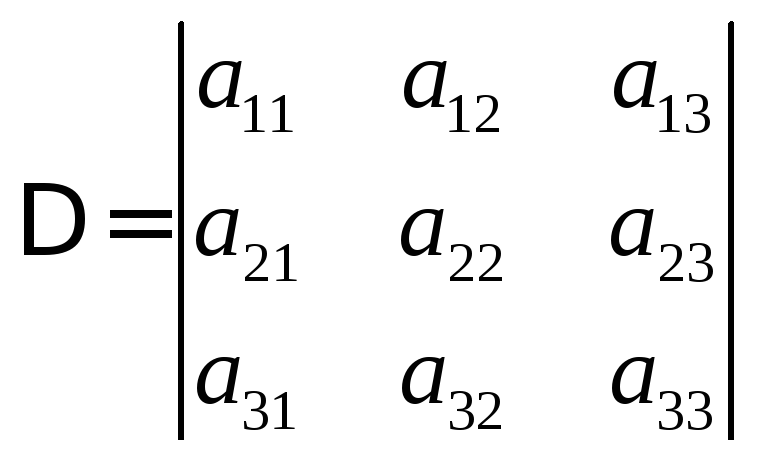Тогда 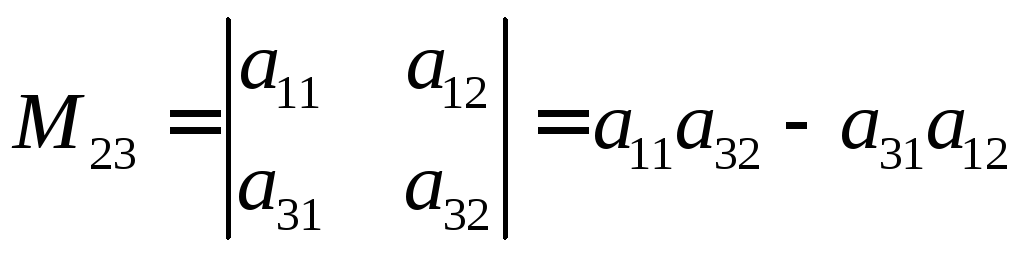или

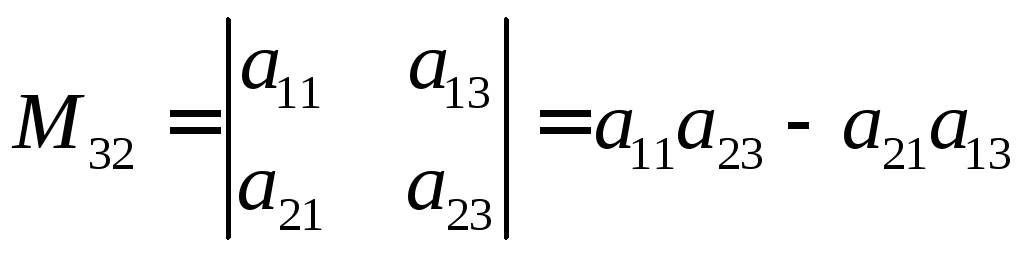
Миноры обозначаем M_ik. Здесь i – номер строки, а k – номер столбца.

Например М₁₃ – 1-я строка, 3-й столбец.

Алгебраическим дополнением элемента a_ik называется величина А_ik, определяемая равенством A_ik = (-1)^i+k M_ik (т.е. минор взятый со знака + или минус).

Например А₃₁ = (-1) М₃₁ = М ₃₁; А₂₃ = (-1)²⁺³ М₂₃ = -М₂₃; А₁₃ = (-1)¹⁺³ М₁₃ + М₁₃.

Алгебраическое дополнение имеет весьма важное свойство при нахождении величины определителя. Произведение элементов какой-нибудь строки (столбца) на их алгебраические дополнения всегда равна величине определителя.

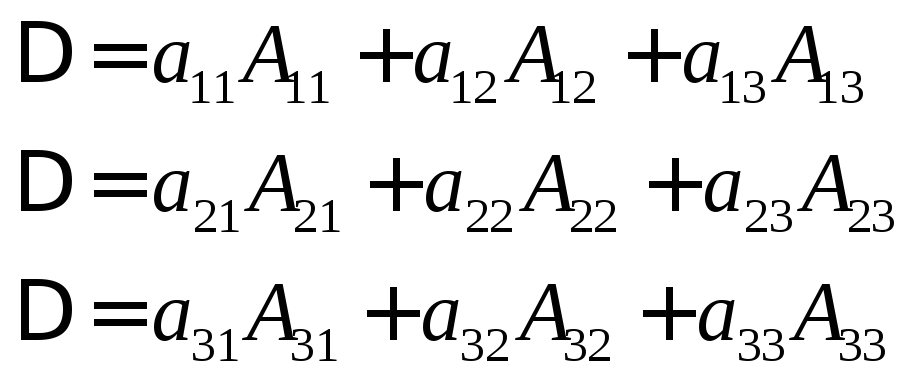
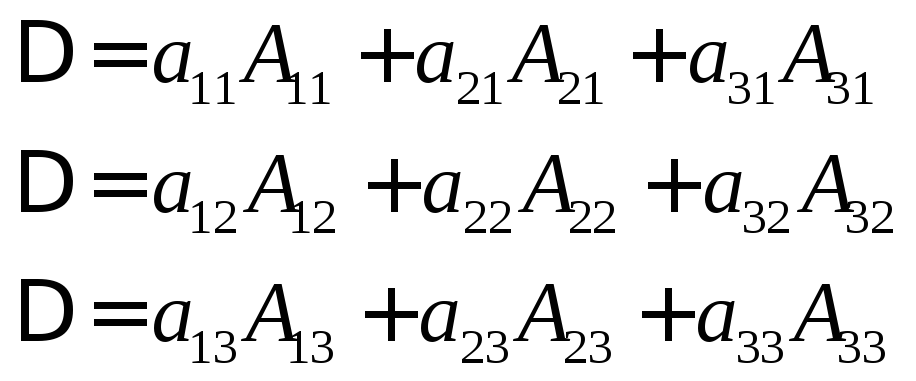
Разложение за элементами строк Разложение за элементами столбцов

Например: Вычислить определитель.

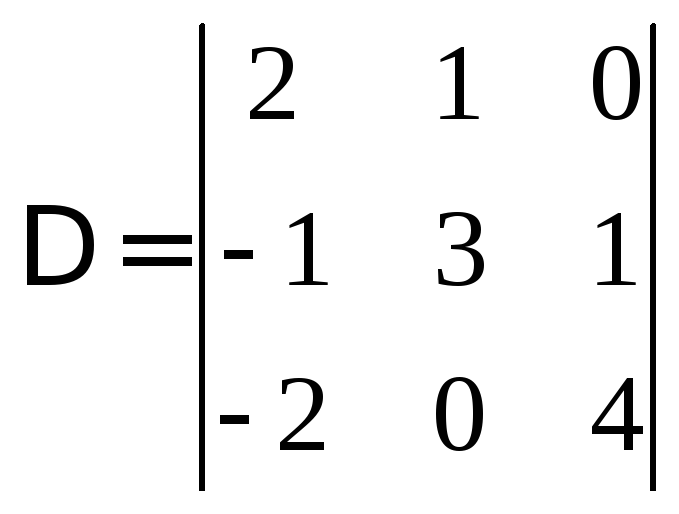Раскрываем его за элементами первой строки ; Тут

Тогда . Мы раньше его подсчитывали.

И еще одно свойство 3-его порядка.

Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

для строки

для столбца

Так как в предыдущем примере

§ 1. Определители высших порядков.

Пусть мы имеем определитель четвертого порядка.

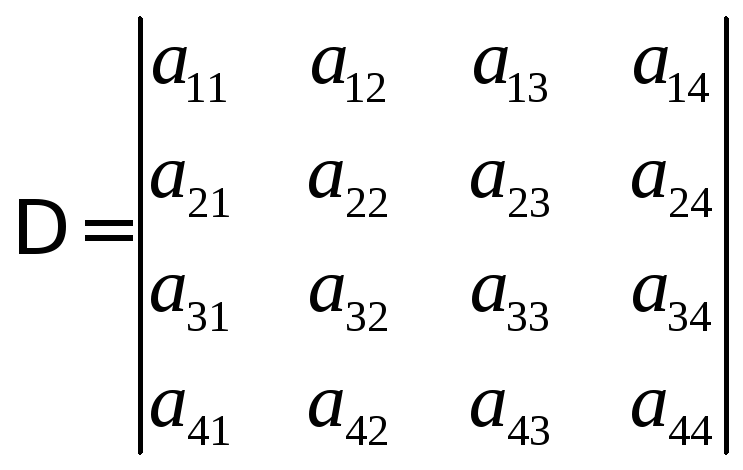Этот определитель можно разложить по элементам любой строки (или столбца). В частности по элементам первой строки это разложение имеет вид

Таких уравнений будет 8. На практике вначале преобразовывают определитель так, чтобы в одной строке (или столбце) все элементы кроме одного были равны нулю. Разлагая тогда этот определитель за элементами упомянутой строки (или столбца), получим только одно слагаемое (остальные будут равны нулю).

Например

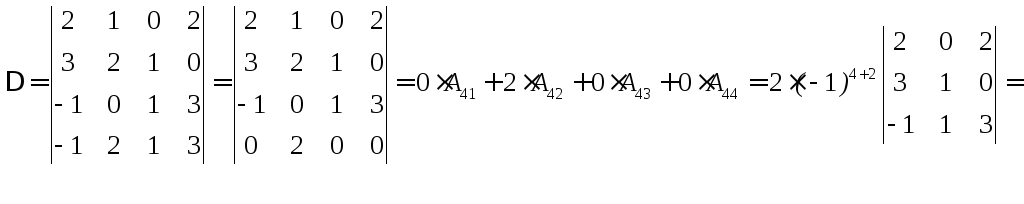
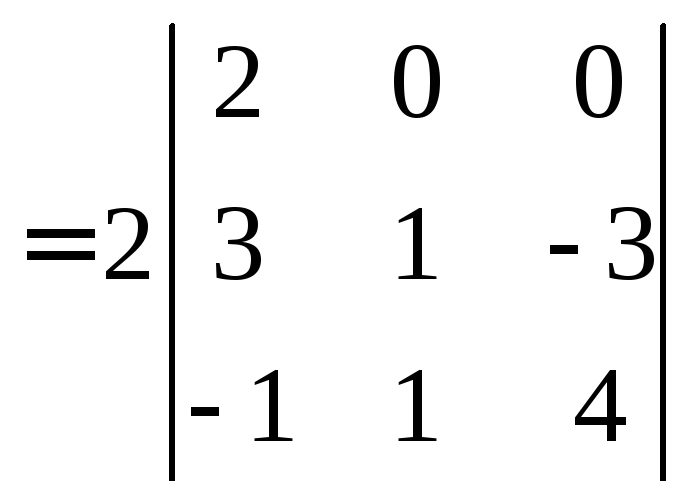
Аналогично вычисляют определители 5-го и высших порядков.

Система двух уравнений с двумя неизвестными

Рассмотрим систему двух уравнений первой степени с двумя неизвестными х и у.

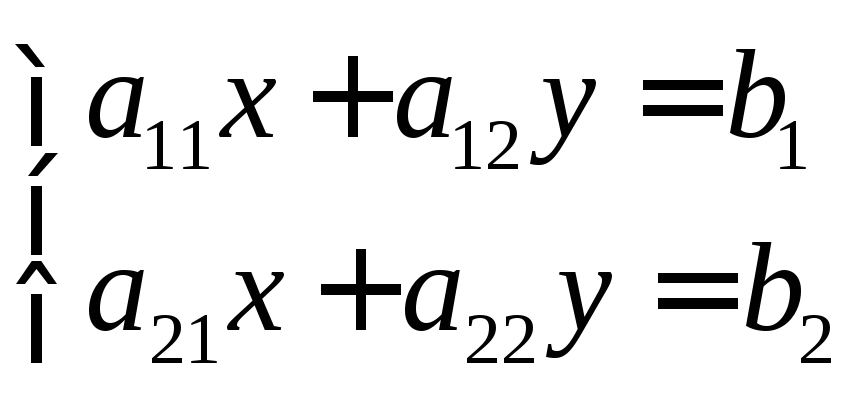(1) Здесь a_ik – постоянные коэффициенты, а b_i – свободные члены.

Сначала умножим первое уравнение на а₂₂, а второе на (-а₁₂) и сложим их почленно

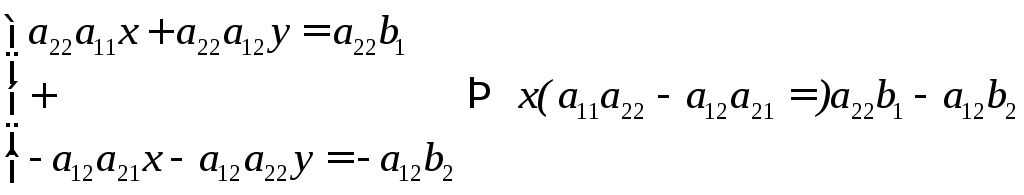(2)

Рассмотрим определитель 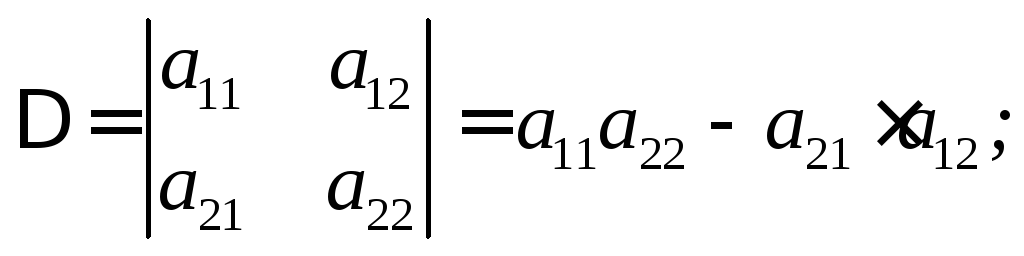если в этом определителе коэффициенты при х заменить столбцом из вольных членов, получим

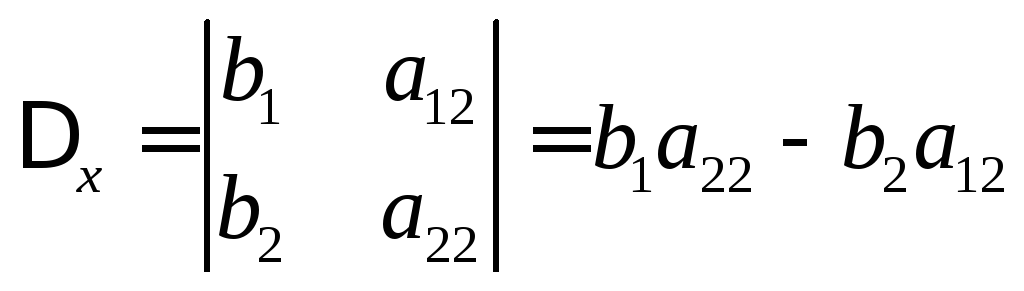. Тогда уравнение (2) принимает вид или (3)

Умножим теперь в системе (1) первое уравнение на (-а₂₁), а второе на а₁₁ и сложим их

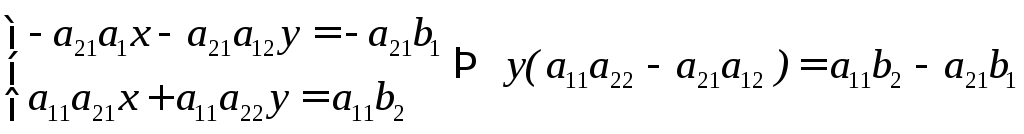(4)

В последнем уравнении

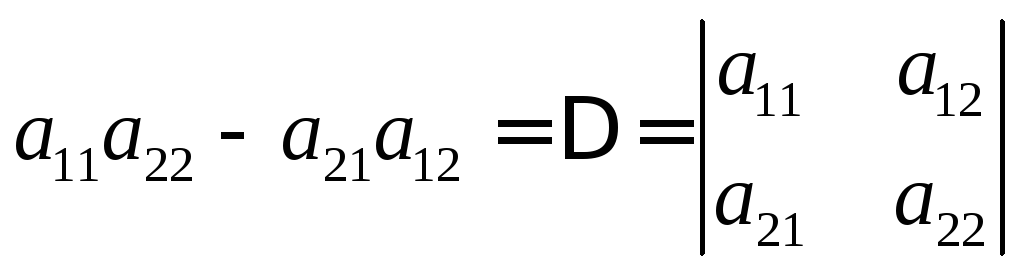
Заменим в этом определителе коэффициенты при «у» столбцом из свободных членов

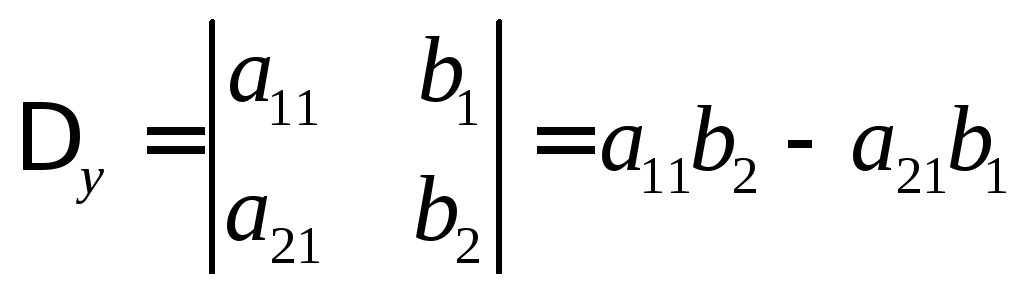. Тогда уравнение (4) принимает вид: или (5)

Это так называемые формулы Крамера.

Пример

. Проверка: .

При решении подобных систем могут быть следующие случаи.

1) . Тогда система (1) имеет единственное решение.

2) Система имеет бесчисленное множество решений

. Здесь

3) , но или . Тогда система (1) не имеет решения

. Система несовместна, т.е. не имеет решений.