Геометрический смысл производной.

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М₀ (см. рисунок). Рассмотрим другую точку М этой кривой и проведем секущую M₀M. Если точка М начинает перемещаться по кривой, а точка М₀ остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая стремится занять положение определенной прямой М₀Т, то прямая М₀Т называется касательной к кривой в данной точке М₀.

Т.о., касательной к кривой в данной точке М₀ называется предельное положение секущей М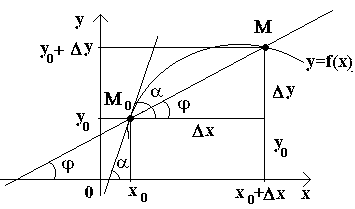₀М, когда точка М стремится вдоль кривой к точке М₀.

Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х₀ функция принимает значение y₀=f(x₀). Этим значениям x₀ и y₀ на кривой соответствует точка М₀(x₀;y₀). Дадим аргументу x₀ приращение Δх. Новому значению аргумента соответствует наращенное значение функции y₀+Δy=f(x₀+Δx). Получаем точку М(x₀+Δx; y₀+Δy). Проведем секущую М₀М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .

Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М₀. Тогда секущая М₀М будет стремиться занять положение касательной к кривой в точке М₀, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

т.е. .

Т.о., геометрически у '(x₀) представляет угловой коэффициент касательной к графику этой функции в точке x₀, т.е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М₀ (x; y) с положительным направлением оси Ox.

Пример.

Найти угловой коэффициент касательной к кривой у = х² в точке М(-1; 1).

Ранее мы уже видели, что (x²)' = 2х. Но угловой коэффициент касательной к кривой есть tg α = y'|_x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ.

НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

Доказательство. Если , то ,

где бесконечно малая величина, т.е. величина, стремящаяся к нулю при . Но тогда при , т.е. при , а это и означает, что функция непрерывна в точке x₀. Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Р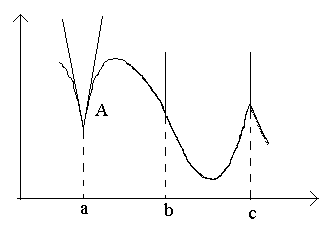ассмотрим на рисунке точкиа, b, c.

В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками.

В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" c вертикальной касательной.

В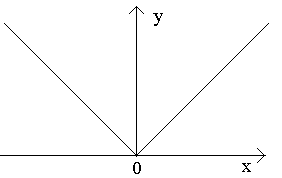точкеc односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.

Примеры.

1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке x = 0, т.к. .

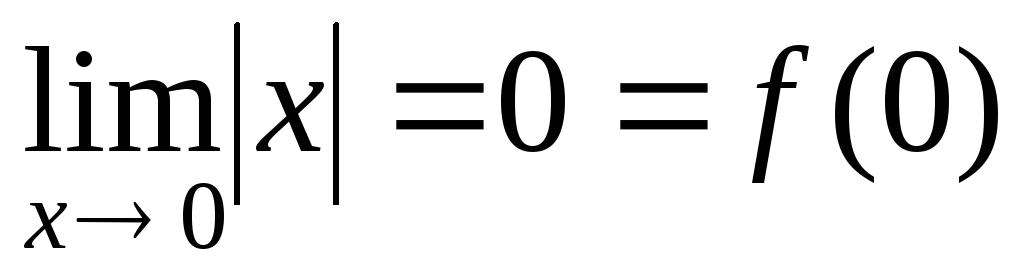Покажем, что она не имеет производной в этой точке.

f(0+Δx) = f(Δx) = |Δx|. Следовательно, Δy = f(Δx) – f(0) = |Δx|

Но тогда при Δx<0 (т.е. при Δx стремящемся к 0 слева)

А при Δx > 0

Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция 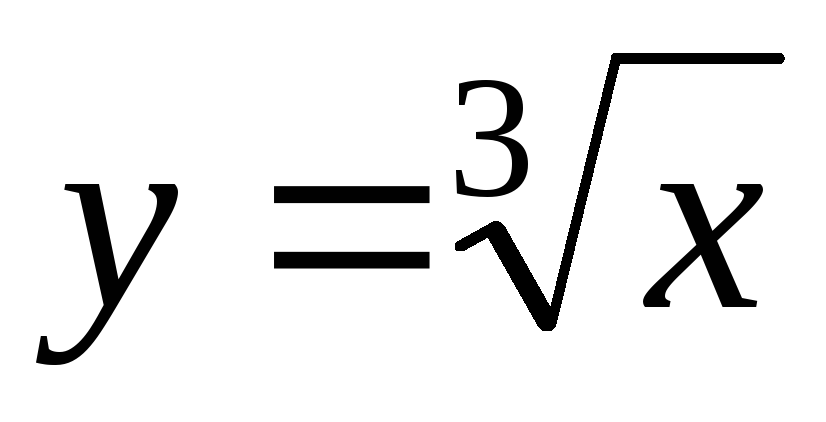определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

При х=0 y=0, при х=0+∆х .

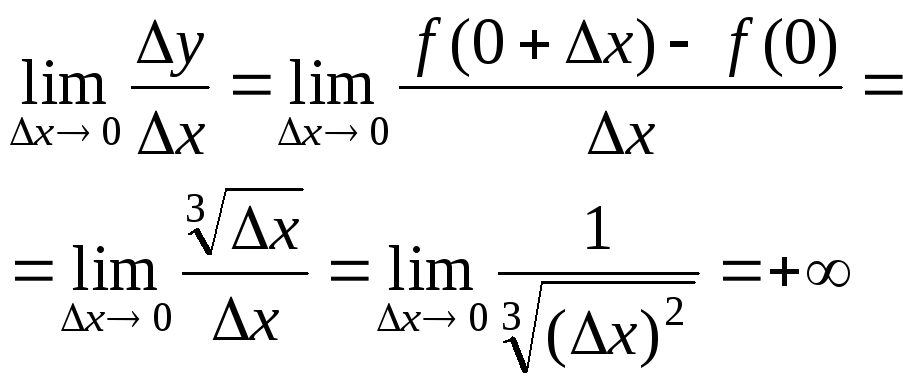
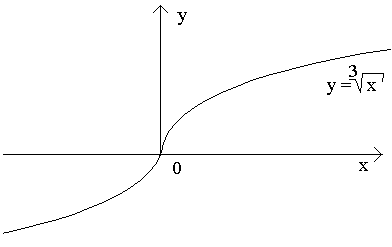
Следовательно, рассматриваемая функция не дифференцируема в точке x=0. Касательная к кривой в этой точке образует с осью абсцисс угол π/2, т.е. совпадает с осью Oy.

Правила и формулы дифференцирования функций.

Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. В качестве примера вычислим производные некоторых функций.

1. Линейная функция .

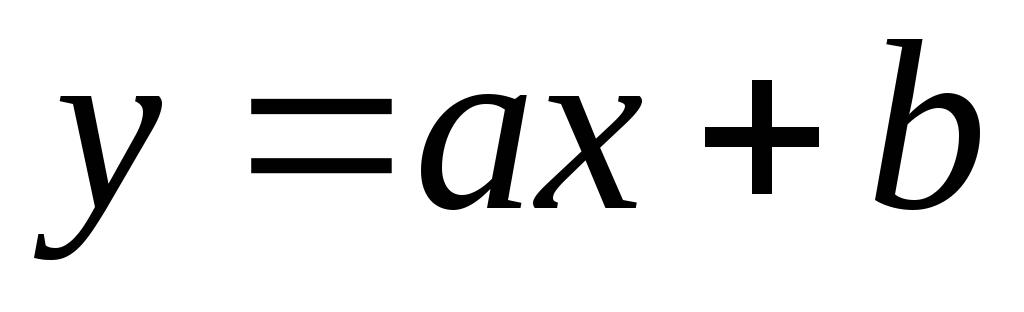Дадим х приращение ∆х, получим х+∆х, ,

. По определению производной:

, таким образом (скорость изменения линейной функции постоянна).

2) у=С (С – константа). , следовательно .

производная от постоянной функции равна нулю.

Нахождение производных по определению часто связано с определенными трудностями. На практике функции дифференцируются с помощью ряда правил и формул. Пусть и=и(х) и v=v(x) две дифференцируемые функции от переменной х.

Теорема 1. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций, т.е. .

Доказательство:

Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).

Тогда приращение функции у=и+ v

Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.

Следовательно,

.

Аналогично доказывается для разности. Теорема справедлива для конечного числа слагаемых.

Теорема 2. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго.

Доказательство:

Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому

Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).

Т.к. и(х+∆х)=и(х)+∆и

v(x+∆х)=v(x) +∆v получаем

Δy=(u(x)+Δи)·(v(x)+Δv) – u(x)·v(x)= u(x)·v(x)+ u(x)· Δv+v(x)∙ Δи+ Δи ∙Δv- u(x)·v(x)=

= u(x)· Δv+ v(x)∙ Δи+ Δи ∙Δv.

По определению производной

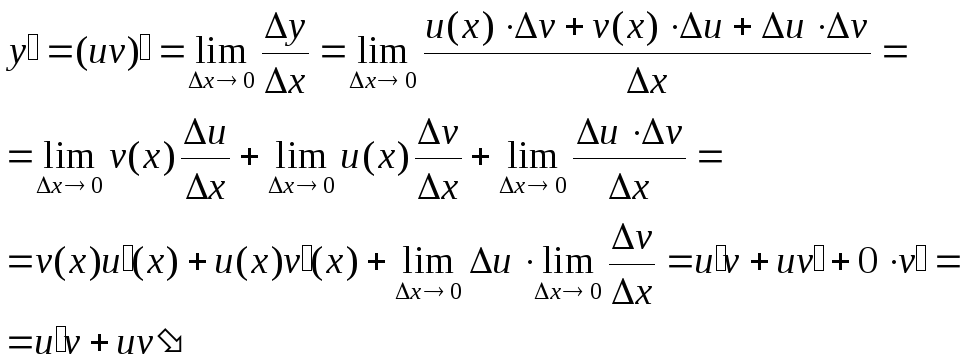
( в силу непрерывности функции ).

На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.

Пусть, например, y=u·v·w. Тогда,

y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.

Следствие: с – const

Теорема 3. Производная частного двух функций , если равна дроби, знаменатель которой равен квадрату данного знаменателя, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя.

Доказательство:

Пусть . Тогда .

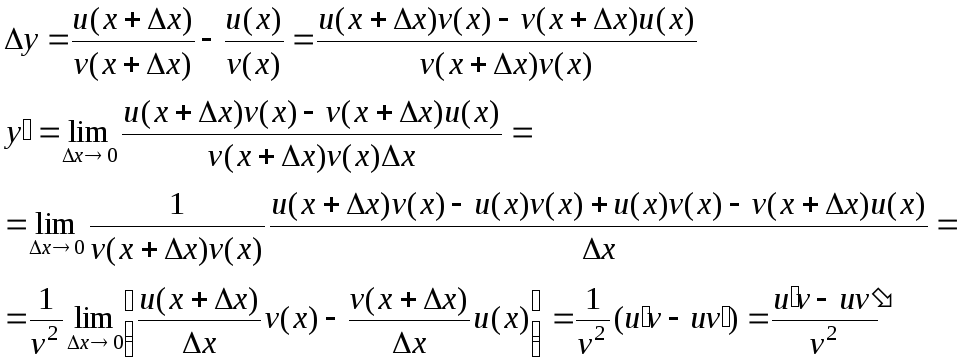
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.

Следствие: 1) 2) с – const