Основные теоремы о пределах.

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

Пример. .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Пример. .

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

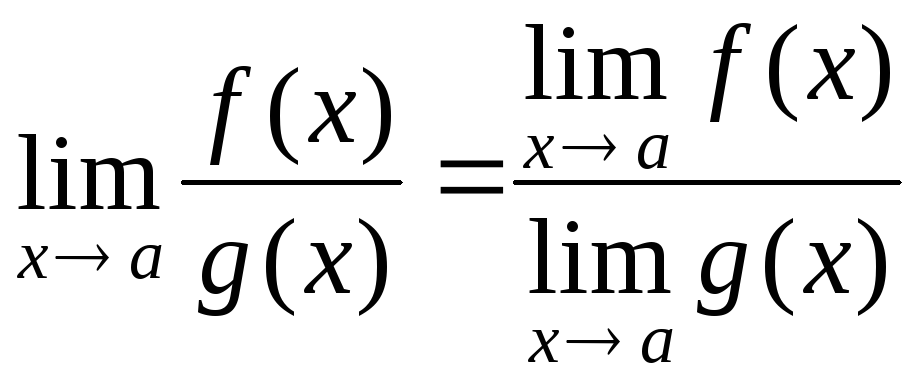, если .

Примеры.

1. .

2. .

3. 

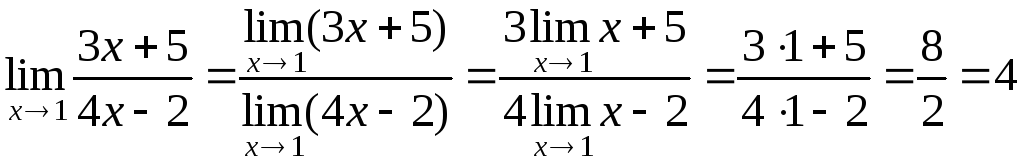
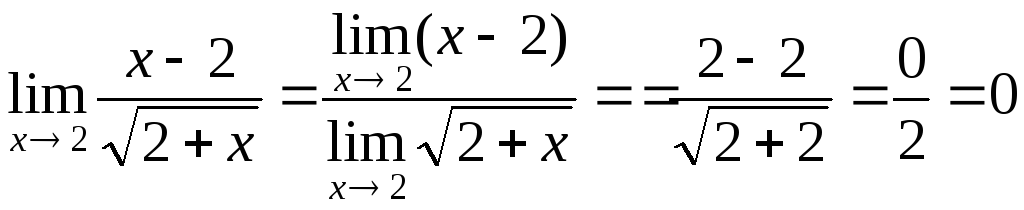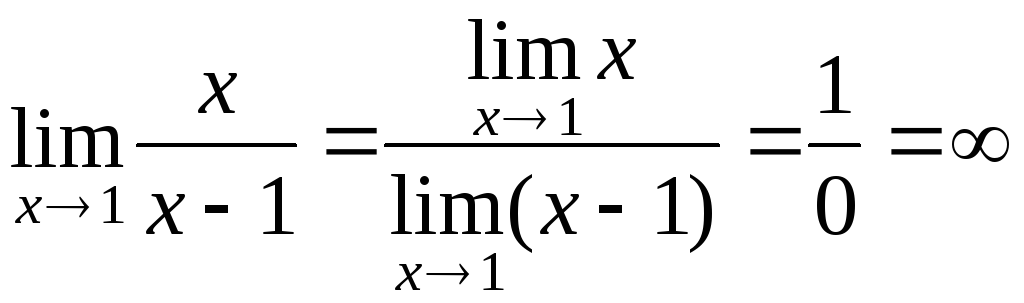
Типы неопределенностей и способы их раскрытия.

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.

Условные выражения

характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.

Рассмотрим некоторые приемы раскрытия неопределенностей.

I. Неопределенность .

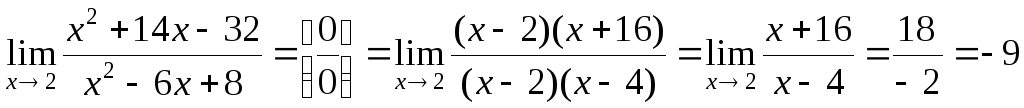1. Числитель и знаменатель разложили на множители. Общий множитель 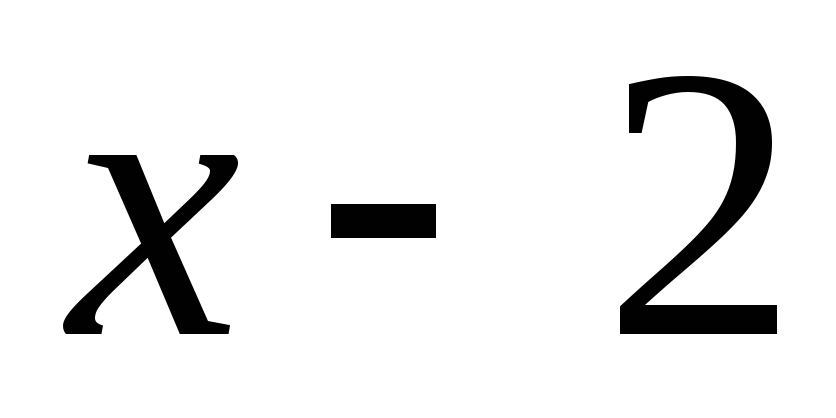сократили, т.о. ушли от неопределенности.

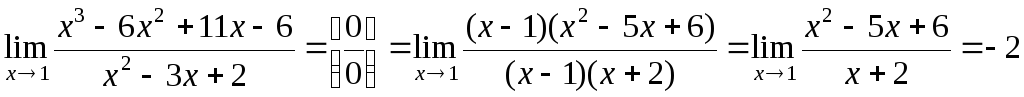2. При разложении числителя на множители воспользовались правилом деления многочлена на многочлен «углом». Так как число x=1 является корнем многочлена x³ – 6x² + 11x– 6, то при делении получим

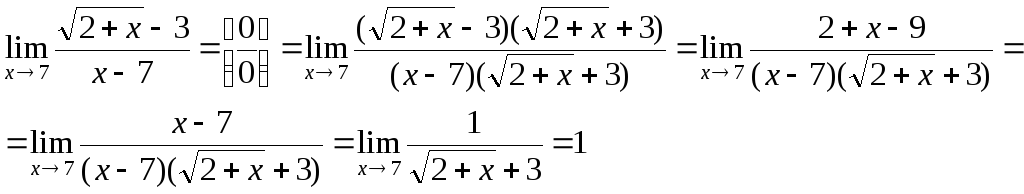3. Числитель и знаменатель умножили на выражение сопряженное числителю.

II. Неопределенность .

1. .

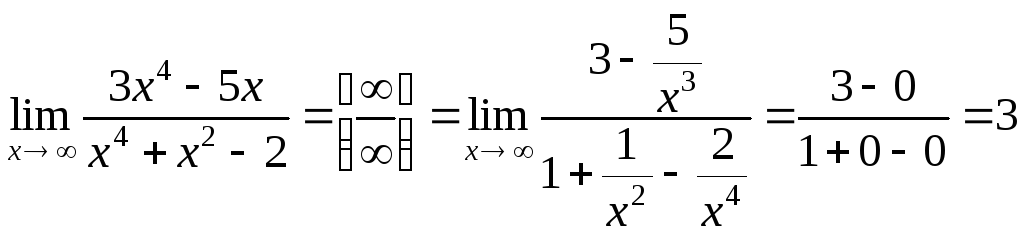При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.

2. .

3. 

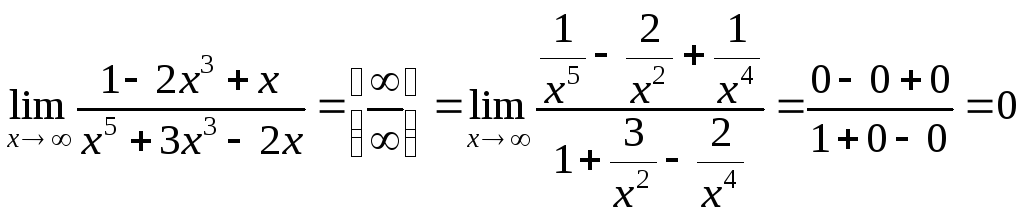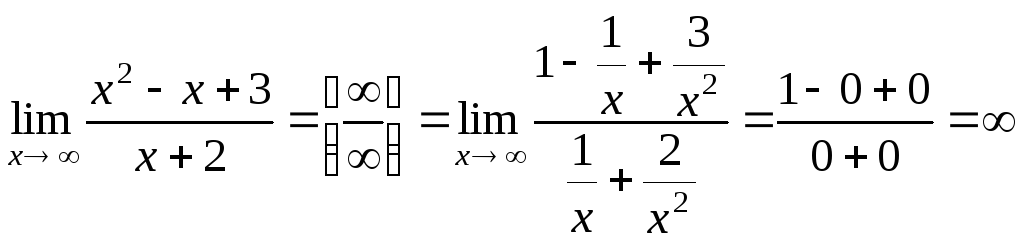
Следующие виды неопределенностей с помощью алгебраических преобразований функции, стоящей под знаком предела, сводят к одному из рассмотренных выше случаев или .

III. Неопределенность  

IV. Неопределенность ∞ –∞.

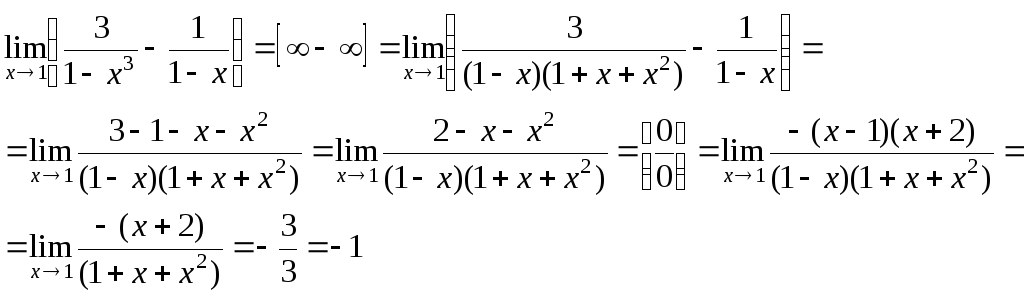
Первый замечательный предел.

Читается: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю.

Примеры:

1.

2.

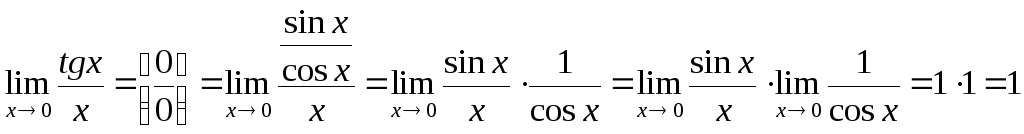
Второй замечательный предел.

(Раскрытие неопределенности .)

(*)

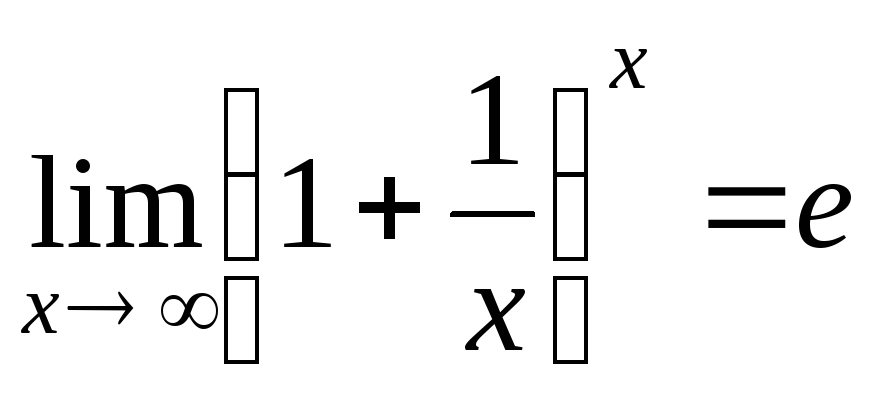
Если положить (при), получим равенство

(**)

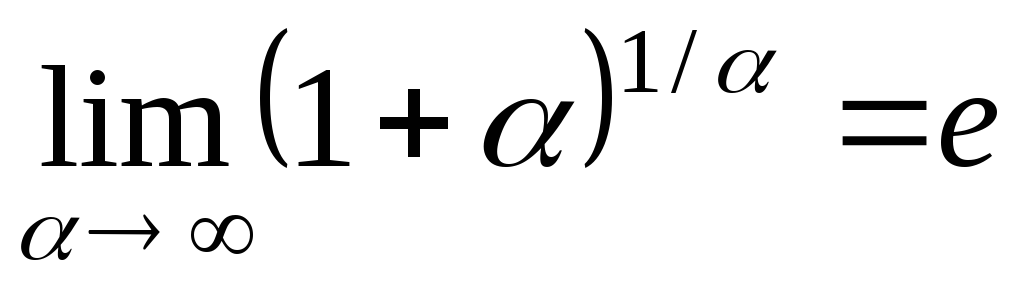
Равенства (*) и (**) называют вторым замечательным пределом.

Пример:

С числом е связана система логарифмов, более удобная, чем десятичная.

(называется натуральный логарифм).

Число е называют ещё неперовым числом (по имени одного из первых изобретателей логарифмических таблиц Непера (1550-1617)). Показательная функция играет большую роль при изучении различных явлений в механике (теория колебаний), в электротехнике, радиотехнике. Функцию часто называют экспонентой и обозначают .

Эквивалентные бесконечно малые и основные теоремы о них.

Опр. Бесконечно малые функции и называются эквивалентными, если . Обозначают ~ .

Например:

~ при , так как ;

~ при , так как .

Приведем ещё примеры эквивалентных бесконечно малых функций.

1) Покажем, что при . Используем для этого определение эквивалентных функций:

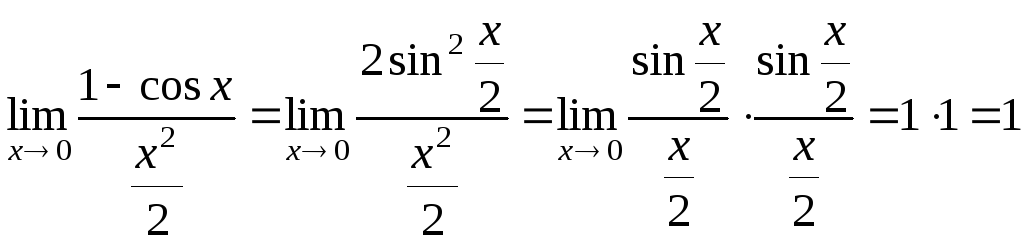
2) при . .

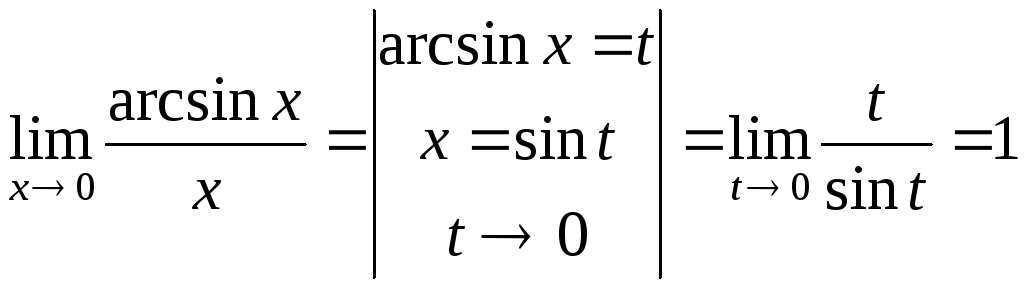Применяются эквивалентные бесконечно малые функции при вычислении пределов, для раскрытия неопределенностей .

Теорема: Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Пример: .

Важнейшие эквивалентности, которые используются при вычислении пределов, приведены в таблице.

1.		6.
2.		7.
3.		8.
4.		9.
5.		10.	(k>0) в частности