
- •Высшая математика конспект лекций
- •1 Курс, 1 семестр
- •Содержание
- •Тема 1 «Элементы линейной алгебры» 7
- •Тема 2 «Элементы векторной алгебры» 22
- •Тема 3 «Элементы аналитической геометрии» 30
- •Тема 4 «Введение в анализ» 51
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» 66
- •Введение
- •Тематический план
- •§ 2. Определители 3-го порядка
- •§ 3. Миноры и алгебраические дополнения
- •§ 1. Определители высших порядков.
- •Система двух уравнений с двумя неизвестными
- •Система 3-х уравнений первой степени с 3-мя неизвестными
- •Понятие о матрицах
- •Сложение матриц и умножение их на число
- •Транспонирование матриц
- •Перемножение матриц
- •Решение систем линейных уравнений методом Гаусса
- •Решение систем 3-х уравнений с 3-мя неизвестными с помощью формул Крамера
- •Исследование систем линейных уравнений
- •§ 1. Общие понятия. Систему уравнений вида
- •§ 2. Система 2-х уравнений с 2-мя неизвестными
- •§ 3. Система 3-х уравнений с 3-мя неизвестными
- •Вопросы для самоконтроля
- •Тема 2 «Элементы векторной алгебры» Основные понятия
- •Линейные операции над векторами
- •Линейная зависимость и независимость векторов
- •Определение координат вектора в данном базисе
- •Системы координат и скалярное произведение векторов Декартова система координат
- •Полярная система координат
- •Скалярное произведение векторов.
- •Векторно-скалярное (смешанное) произведение
- •§ 1. Вычисление объема параллелепипеда
- •§3.Направляющие косинусы
- •Вопросы для самоконтроля
- •Тема 3 «Элементы аналитической геометрии»
- •П 4. Переход от полярных координат к декартовым и обратно
- •Простейшие задачи аналитической геометрии на плоскости п 1. Проекция отрезка на оси координат
- •П 2 .Расстояние между двумя точками на координатной плоскости
- •П 3. Деление отрезка в данном отношении
- •Линии и их уравнения п 1. Понятие уравнения линии
- •П 2. Примеры заданий линий при помощи уравнений
- •П 3. Получение линии как геометрического места точек
- •П 4. Параметрические уравнения линий
- •П 5. Алгебраические линии
- •Прямая на плоскости п 1. Угловой коэффициент
- •П 3. Уравнение прямой, проходящей через данную точку м1 (х1; у1)
- •П 8. Уравнение прямой в отрезках
- •П 9. Нормальное уравнение прямой
- •П. 10. Расстояние от точки до прямой
- •П. 11. Уравнение прямой в полярных координатах
- •П. 3 Эллипс и его каноническое уравнение
- •П.4 Эксцентриситет и директрисы эллипса
- •Гипербола и ее каноническое уравнение
- •П 6. Асимптоты гиперболы
- •П 7. Эксцентриситет и директрисы гиперболы
- •П. 8 Парабола и ее уравнение
- •П. 9 Уравнение эллипса, гиперболы и параболы в полярных координатах
- •Преобразование координат п. 1 Преобразование координат при параллельном сдвиге осей
- •П 3. Преобразование декартовых координат при изменении начала и поворота осей
- •П. 4 Преобразование общего уравнения второй степени не содержащего произведения переменных
- •П 5. Преобразование общего уравнения второго порядка
- •Аналитическая геометрия в пространстве Уравнение прямой
- •Понятие об уравнении плоскости.
- •Уравнения поверхностей
- •Вопросы для самоконтроля
- •Тема 4 «Введение в анализ» Переменные и постоянные величины. Понятие функции.
- •Основные характеристики функций.
- •Основные элементарные функции и их графики.
- •Числовая последовательность.
- •Предел функции.
- •Бесконечно малые величины.
- •Бесконечно большие функции.
- •Соотношение между бесконечно малыми и бесконечно большими функциями.
- •Основные теоремы о пределах.
- •Типы неопределенностей и способы их раскрытия.
- •Первый замечательный предел.
- •Эквивалентные бесконечно малые и основные теоремы о них.
- •Непрерывность функций.
- •Основные теоремы о непрерывных функциях.
- •Вопросы для самоконтроля
- •Тема 5 «Элементы дифференциального исчисления функции одной переменной» Определение производной.
- •Геометрический смысл производной.
- •Производные основных элементарных функций.
- •Производная сложной и обратной функции.
- •Дифференцирование неявно заданной функции.
- •Дифференцирование функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Производные высших порядков.
- •Производные высших порядков неявно заданной функции.
- •Производные высших порядков от функций заданных параметрически.
- •Дифференциал функции.
- •Правила вычисления дифференциала.
- •Приложения производной.
- •Исследование функций при помощи производной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Вопросы для самоконтроля
- •Литература
Основные элементарные функции и их графики.
Показательная
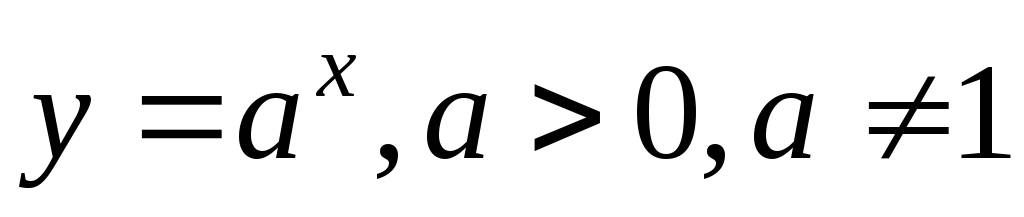
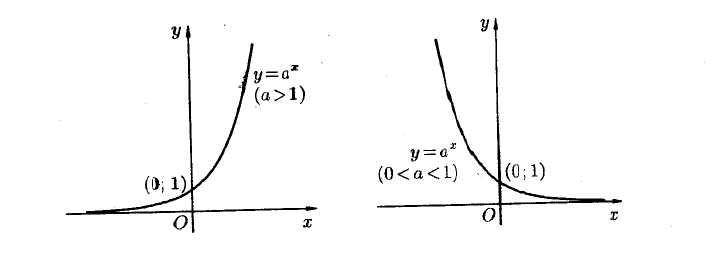
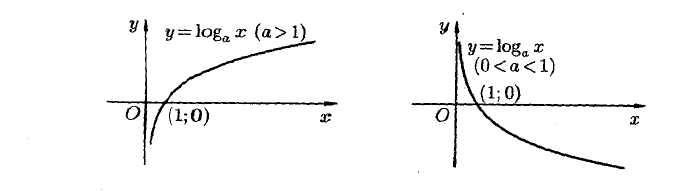 Логарифмическая
функция
Логарифмическая
функция
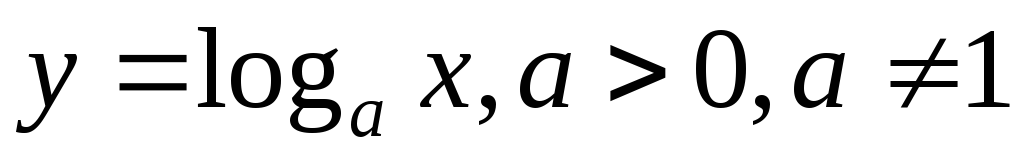
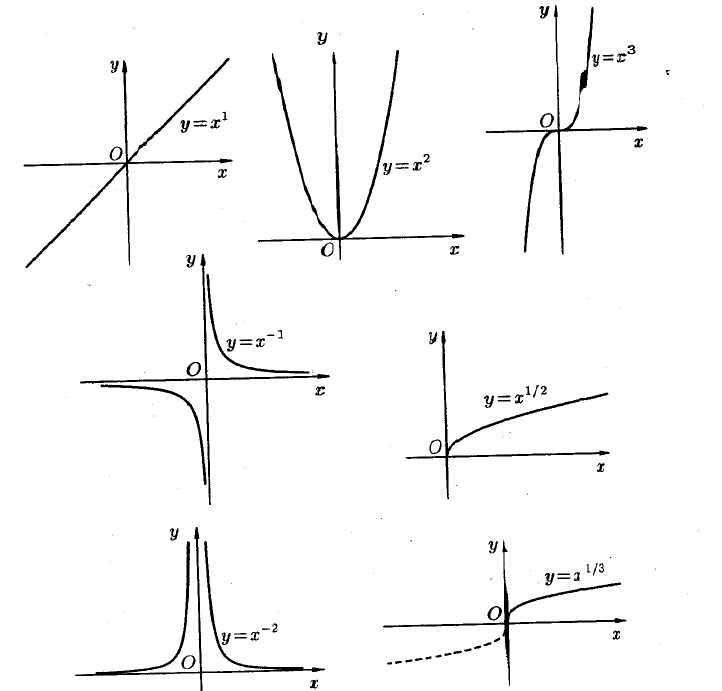
Степенная функция
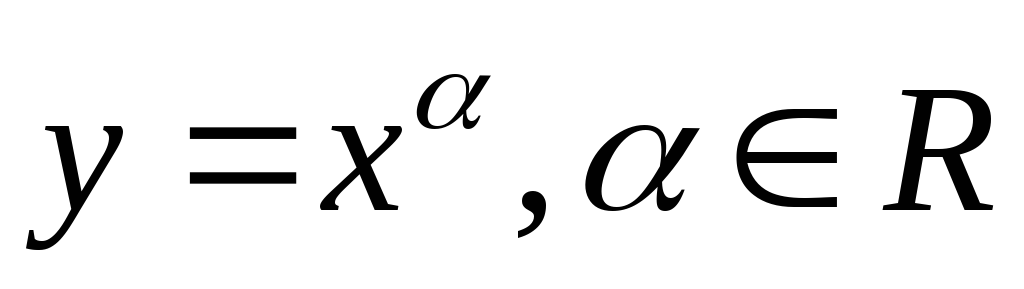
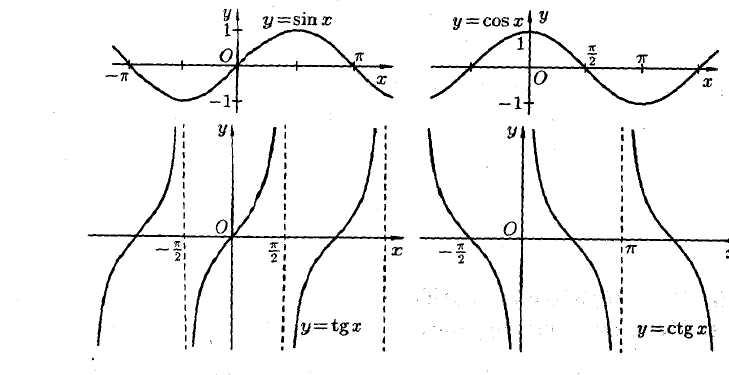 Тригонометрические
функции
Тригонометрические
функции
![]()
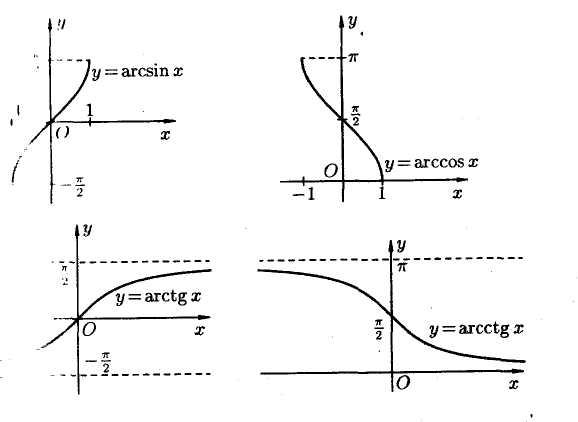 Обратные
тригонометрические функции
Обратные
тригонометрические функции
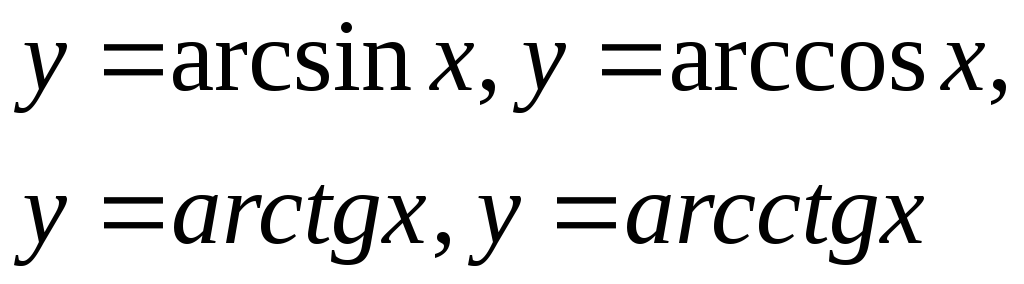
Опр. Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операции взятия функции от функции, называется элементарной функцией.
Примеры элементарных функций:
![]() .
.
Примеры не элементарных функций:
![]() ;
;
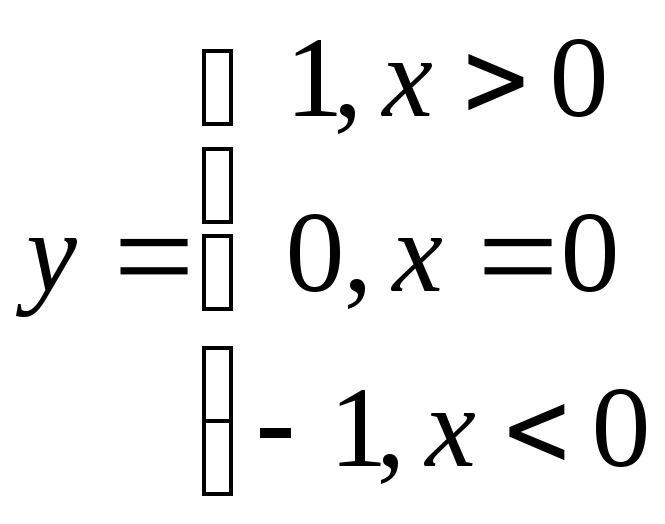 .
.
Числовая последовательность.
Опр.
Под числовой
последовательностью
![]() понимается функция
понимается функция
![]() ,
заданная на множестве натуральных чисел
N.
,
заданная на множестве натуральных чисел
N.
Обозначают:
![]() .
.
![]() -
первый член последовательности,
-
первый член последовательности,
![]() - второй член последовательности, …,
- второй член последовательности, …,
![]() - общий или n–й
член последовательности. Чаще всего
последовательность задается формулой,
которая позволяет вычислить любой член
последовательности.
- общий или n–й
член последовательности. Чаще всего
последовательность задается формулой,
которая позволяет вычислить любой член
последовательности.
Например:
1)
![]()
![]() и т.д.
и т.д.
Получаем
числовую последовательность 2, 5, 10, 17,
…,
![]() ,
…
,
…
2)
![]()
![]()
3)
![]() -1, 1, -1, 1 ,-1, ….
-1, 1, -1, 1 ,-1, ….
Опр.
Последовательность
![]() называется ограниченной,
если существует такое число М>0,
что для любого
называется ограниченной,
если существует такое число М>0,
что для любого
![]()
![]() .
В противном случае – не ограниченной.
.
В противном случае – не ограниченной.
Пример:
![]() М=1
М=1
![]()
![]() .
.
Опр.
Последовательность
![]() называется возрастающей,
если для любого
называется возрастающей,
если для любого![]() выполняется неравенство
выполняется неравенство
![]() ;
убывающей
;
убывающей
![]() .
.
Опр.
Если все элементы последовательности
![]() равны одному и тому же числу С,
то она называется постоянной.
равны одному и тому же числу С,
то она называется постоянной.
Например,
![]() 1, 1, 1, …..
1, 1, 1, …..
Опр.
Число а
называется
пределом числовой последовательности
![]() ,
если для любого
,
если для любого
![]() существует такое натуральное число N,
что при всех
существует такое натуральное число N,
что при всех
![]() выполняется неравенство
выполняется неравенство
![]() .
Пишут
.
Пишут
![]() .
.
Геометрически:
число а
называется
пределом последовательности
![]() ,
если для любой
,
если для любой
![]() -окрестности
точки а
найдется натуральное число N,
что все значения
-окрестности
точки а
найдется натуральное число N,
что все значения
![]() ,
для которых
,
для которых
![]() ,
попадут в
,
попадут в
![]() -окрестность
точки а;
чем меньше
-окрестность
точки а;
чем меньше
![]() ,
тем больше N,
но в любом случае в
,
тем больше N,
но в любом случае в
![]() -окрестности
точки а
находится бесконечное число членов
последовательности, а вне её может быть
лишь конечное их число.
-окрестности
точки а
находится бесконечное число членов
последовательности, а вне её может быть
лишь конечное их число.
Пример.
Пусть переменная величина x последовательно принимает значения
![]()
Докажем,
что предел этой числовой последовательности
равен 1. Возьмем произвольное положительное
число ε.
Нам нужно найти такое натуральное число
N,
что при всех
![]() выполняется неравенство
выполняется неравенство
![]() .
Действительно, т.к.
.
Действительно, т.к.
![]() ,
то для выполнения соотношения
,
то для выполнения соотношения
![]() достаточно, чтобы
достаточно, чтобы
![]() или
или
![]() .
Поэтому, взяв в качестве N
любое натуральное число, удовлетворяющее
неравенству
.
Поэтому, взяв в качестве N
любое натуральное число, удовлетворяющее
неравенству
![]() ,
получим что нужно. Так если взять,
например,
,
получим что нужно. Так если взять,
например,
![]() ,
то, положив N=6,
для всех
,
то, положив N=6,
для всех
![]() будем иметь
будем иметь
![]() .
.
Сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся.
Пример
расходящейся последовательности:
![]() ;
;
![]()
Теорема. Всякая монотонная ограниченная последовательность имеет предел.
Пример:
1)
![]() .
Последовательность возрастающая
(монотонная)
.
Последовательность возрастающая
(монотонная)
![]() и ограниченная
и ограниченная
![]() .
Предел последовательности равен единице
.
Предел последовательности равен единице
![]() .
.
2)
![]()
![]() .
.
Предел функции.
Опр.
Пусть
![]() –
любое действительное число. Окрестностью
точки
–
любое действительное число. Окрестностью
точки
![]() называется любой интервал
называется любой интервал
![]() ,
содержащий точку
,
содержащий точку
![]() .
В частности, интервал
.
В частности, интервал
![]() ,
где
,
где
![]() ,
называется
,
называется
![]() -
окрестностью точки
-
окрестностью точки
![]() .
.
Если
![]() то выполняется неравенство
то выполняется неравенство
![]() или, что то же,
или, что то же,
![]() .
Выполнение последнего неравенства
означает попадание точки х
в
.
Выполнение последнего неравенства
означает попадание точки х
в
![]() -окрестность
точки
-окрестность
точки
![]() .
.
Опр.
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
![]() .
Число
А называется пределом функции
.
Число
А называется пределом функции
![]() в точке
в точке
![]() (или при
(или при
![]() ),
если для любого положительного числа
),
если для любого положительного числа![]() найдется такое положительное число
найдется такое положительное число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
Записывают
.
Записывают
![]() .
.
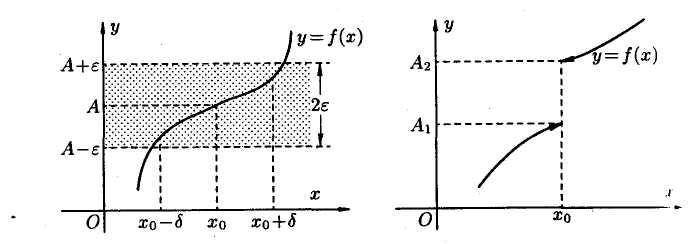
Геометрический
смысл предела: точки графика функции
![]() лежат внутри полосы шириной 2
лежат внутри полосы шириной 2![]() ,
ограниченной прямыми
,
ограниченной прямыми
![]() .
Величина
.
Величина
![]() зависит
от выбора
зависит
от выбора
![]() ,
т.е.
,
т.е.
![]() .
.
Опр.
Если функция
![]() имеет
пределом число
имеет
пределом число
![]() ,
при условии, что х
стремится
к
,
при условии, что х
стремится
к
![]() ,
оставаясь меньше, чем
,
оставаясь меньше, чем
![]() ,
то принята запись
,
то принята запись
![]() ,
число
,
число
![]() называют односторонним
пределом функции слева.
называют односторонним
пределом функции слева.
Опр.
Если
![]() является пределом функции
является пределом функции
![]() при условии, что х
стремится
к
при условии, что х
стремится
к
![]() ,
оставаясь больше, чем
,
оставаясь больше, чем
![]() ,
то
,
то
![]() называют односторонними
пределом функции справа
и обозначают
называют односторонними
пределом функции справа
и обозначают
![]() .
.
Для
существования предела А
функции
![]() в точке
в точке
![]() необходимо и достаточно, чтобы существовали
в этой точке пределы функции слева и
справа и чтобы они были равны между
собой
необходимо и достаточно, чтобы существовали
в этой точке пределы функции слева и
справа и чтобы они были равны между
собой
![]() .
.
Пример.
Рассмотрим функцию y=f(x), определенную на отрезке [0,4] следующим образом
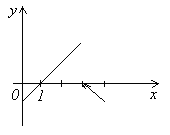
![]()
Найдем пределы функции f(x) при x→3. Очевидно,
![]() ,
а
,
а
![]() ,
т.е. функция в точке х=3
не имеет двустороннего предела.
,
т.е. функция в точке х=3
не имеет двустороннего предела.
Понятие предела функции в бесконечно удаленной точке.
До сих пор мы рассматривали пределы для случая, когда переменная величина x стремилась к определенному постоянному числу.
Будем
говорить, что переменная x
стремится к бесконечности,
если для каждого заранее заданного
положительного числа M
(оно может быть сколь угодно большим)
можно указать такое значение
![]() ,
начиная с которого, все последующие
значения переменной будут удовлетворять
неравенству |x|>M.
,
начиная с которого, все последующие
значения переменной будут удовлетворять
неравенству |x|>M.
Например, пусть переменная х принимает значения x1= –1, x2=2, x3= –3, …, xn=(–1)nn, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M.
Переменная
величина
![]() ,
если при произвольном
,
если при произвольном
![]() все последующие значения переменной,
начиная с некоторого, удовлетворяют
неравенству
все последующие значения переменной,
начиная с некоторого, удовлетворяют
неравенству
![]() .
.
Аналогично,
![]() ,
если при любом
,
если при любом
![]()
![]() .
.
Будем
говорить, что функция
![]() стремится к пределу b
при
стремится к пределу b
при
![]() ,
если для произвольного малого
положительного числа ε
можно указать такое положительное число
M,
что для всех значений x,
удовлетворяющих неравенству
,
если для произвольного малого
положительного числа ε
можно указать такое положительное число
M,
что для всех значений x,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Обозначают
![]() .
.
П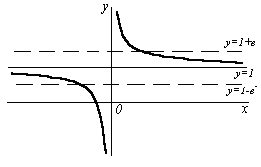 ример.
ример.
Используя
определение, доказать, что
![]() .
.
Нужно
доказать, что при произвольном ε
будет выполняться неравенство
![]() ,
как только
,
как только
![]() ,
причем число М
должно определяться выбором ε.
Записанное неравенство эквивалентно
следующему
,
причем число М
должно определяться выбором ε.
Записанное неравенство эквивалентно
следующему
![]()
![]() ,
которое будет выполняться, если
,
которое будет выполняться, если
![]() .
Это и значит, что
.
Это и значит, что
![]() (см. рис.).
(см. рис.).
