Тема 3 «Элементы аналитической геометрии»

Аналитическая геометрия на плоскости

п 1. Предмет и метод аналитической геометрии

Аналитическая геометрия отличается от элементарной главным образом своим методом.

Элементарная геометрия доказывает теоремы с помощью чертежа; т.е. методом построения.

В аналитической геометрии, опираясь на вывод формулы и установленные правила, все геометрически задачи решаются только с помощью вычислений, не обращаясь к чертежу. Поэтому говорят, что аналитическая геометрия есть геометрия вычисления.

п 2. Система декартовых прямоугольных координат на плоскости

Д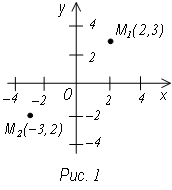ля определения положения точки на плоскости вводят так называемую декартову прямоугольную систему координат ХОУ (рис. 1).

ох – горизонтальная ось (абсцисса)

оу – вертикальная ось (ордината)

оси ох и оу взаимно перпендикулярны

Точка О – точка пересечения осей называется началом координат.

Систему единиц берут обычно одинаковой для обеих осей.

п 3. Полярные координаты

П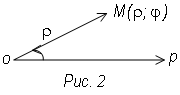олярная система координат определяется заданием некоторой точки О, называемой полюсом; исходящего из этой точки луча ОА. Называемого полярной осью, и масштаба для измерения длины (рис. 2).

Поворот вокруг точки О будет положительным, если он происходит против часовой стрелки.

Рассмотрим произвольную точку М - расстояние от полюса до точки М. φ – угол на который нужно повернуть полярную ось, чтобы она совпала с лучом ОМ. Условимся угол φ брать в пределах .

Тогда в каждой точки плоскости будет соответствовать единственная пара чисел ρ и φ (для полюса ρ = 0; φ – произвольно).

Числа ρ и φ называются полярными координатами точки М. При этом число ρ называется полярными координатами точки М. При этом число ρ называется полярным радиусом; φ – полярным углом.

П 4. Переход от полярных координат к декартовым и обратно

Наша цель, зная полярные координаты некоторой точки, вычислить ее декартовы и обратно, зная декартовы координаты, вычислить полярные координаты.

П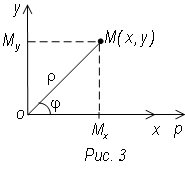усть полюс полярной системы совпадает с началом декартовых координат, а полярная ось совпадает с положительной полуосью абсцисс (рис 3)

Пусть М (х, у) произвольная точка на плоскости. Х и У ее декартовы координаты ρ и φ – полярные.

Опустим из М перпендикуляр на оси х и у

Тогда

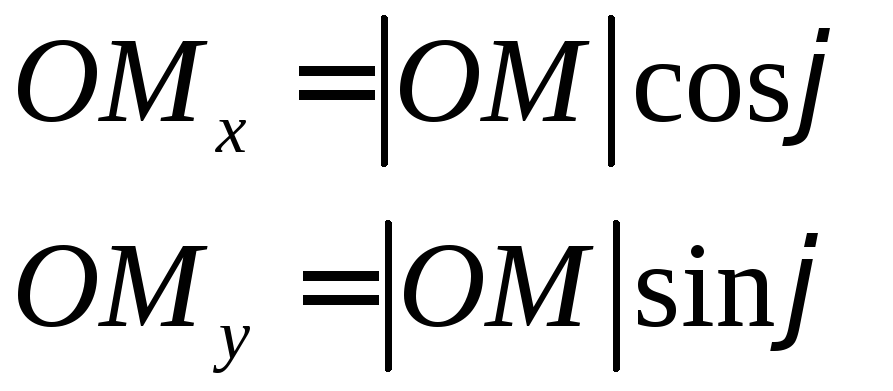
или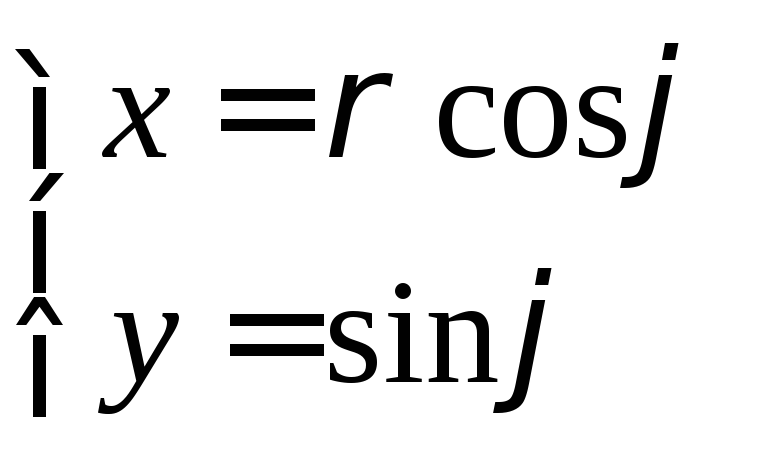 – формулы, выражающие декартовы координаты через полярные.

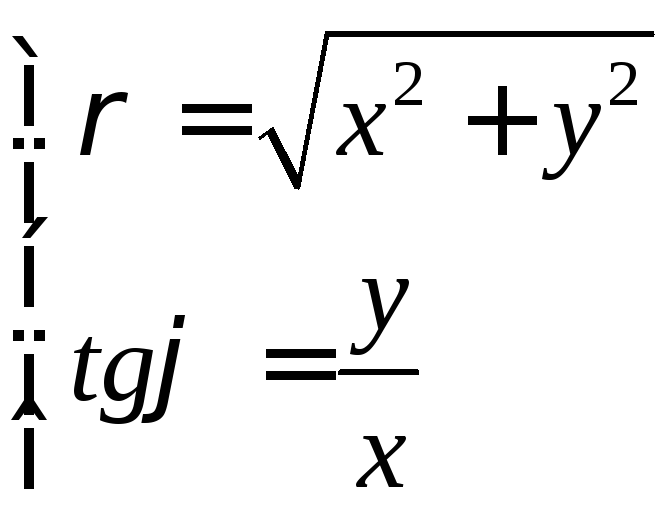–формулы, выражающие полярные координаты через декартовы.

Простейшие задачи аналитической геометрии на плоскости п 1. Проекция отрезка на оси координат

Определение. Прямая, на которой выбрано положительное направление, называется осью (рис. 4).

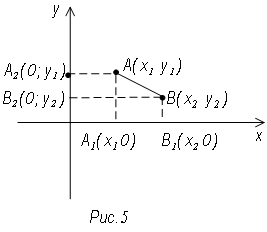Определение. Отрезок АВ называется направленным, если сказано, какая из точек считается началом отрезка, какая концом. Направлением отрезка считается направление от начала к концу .

Рассмотрим произвольный отрезок . (рис. 5)

Пусть А₁ и В₁ – основания перпендикуляров, опущенных из начала и конуса отрезка АВ на ось х.

А₂ и В₂ – основания перпендикуляров, опущенных из начала и конца от отрезка АВ на ось у. В нашем случае направление отрезка А₁ В₁ совпадает с положительным направлением оси ох. Направление отрезка А₂ В₂ противоположному направлению оси оу.

Определение. Число, равное разности х₂ - х₁ назовем проекцией отрезка АВ на ось ох и обозначим символом

Определение. Число, равное разности у₂ – у₁ назовем проекцией отрезка АВ на ось оу и обозначим символом

т.е. проекции отрезка на ох равно разности абсцисс конца и начала отрезка, а проекции отрезка на ось оу равна разности ординат конца и начала от резка.

В нашем случае