52 Вопрос:

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке , а функция g имеет производную в точке , то сложная функция h(x) = g(f(x)) также имеет производную в точке .

Пусть даны функции, определённые в окрестностях на числовой прямой, где и Пусть также эти функции дифференцируемы: Тогда их композиция также дифференцируема: и её производная имеет вид:

Замечание [править]

В обозначениях Лейбница цепное правило для вычисления производной функции где принимает следующий вид:

Инвариантность формы первого дифференциала [править]

Дифференциал функции в точке имеет вид:

где  — дифференциал тождественного отображения :

Пусть теперь Тогда , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

Пусть Тогда функция может быть записана в виде композиции где

Дифференцируя эти функции отдельно:

получаем

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию от аргументов в окрестности точки . Для любого единичного вектора определим производную функции в точке по направлению следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

Связь с градиентом

Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:

,

где — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора .

53 Вопрос:

Для вычисления дифференциалов высших порядков используется следующая символическая формула:

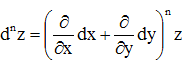
Пример 8. z=y•lnx. Найти 

Найдем частные производные . Дифференцируя повторно, получим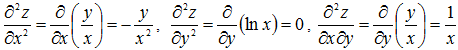 

Пример 9. z=x²•y. Найти d³z

Найдем частные производные

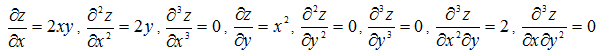
Подставив найденные частные производные в формулу для вычисления d³z, получим:

d³z=0•dx³+3•2•dx²dy+3•0•dx²dy+0•dy³=6dx²dy

Теорема: Смешанные частные производные одной и той же функции, отличающиеся лишь порядком (очерёдностью) дифференцирования, равны между собой при условии их непрерывности. Такое свойство называется равенством смешанных производных

Определение смешанной производной [править]

Пусть дана достаточно гладкая (скалярная) функция многих переменных:

Мы можем взять частную производную этой функции по одному из аргументов , считая остальные аргументы постоянными параметрами. В результате мы получим новую функцию:

Эта новая функция тоже зависит от остальных аргументов, как от параметров. То есть численное значение в общем случае зависит от тех же переменных , что и оригинальная функция :

Если функция окажется достаточно гладкой, то мы можем и её продифференцировать, взяв частную производную по тому же самому, или по другому аргументу :

Если , то выражение в правой части равенства (4) называется смешанной производной.

Основа теоремы [править]

Для достаточно гладкой функции многих переменных значение смешанной производной не зависит от порядка дифференцирования:

Теорема является базовой в теории функций многих переменных и широко применяется в математической физике, теории дифференциальных уравнений в частных производных, дифференциальной геометрии.