
- •35 Вопрос:
- •36 Вопрос:
- •37 Вопрос:
- •39 Вопрос:
- •40 Вопрос:
- •41 Вопрос:
- •42 Вопрос:
- •43 Вопрос:
- •44 Вопрос:
- •45 Вопрос:
- •12.1. Несобственные интегралы по неограниченному промежутку
- •46 Вопрос:
- •47 Вопрос:
- •49 Вопрос:
- •50 Вопрос:
- •51 Вопрос:
- •52 Вопрос:
- •Связь с градиентом
- •53 Вопрос:
- •54 Вопрос:
- •Дифференциал высшего порядка функции одной переменной[править]
- •Дифференциал высшего порядка функции нескольких переменных[править]
- •55 Вопрос:
- •Необходимые условия существования локальных экстремумов [править]
- •Достаточные условия существования локальных экстремумов [править]
- •56 Вопрос:
- •57 Вопрос: Теорема об обратной функции.
46 Вопрос:
Сходящийся ряд
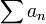 называется
сходящимся абсолютно, если сходится
ряд из модулей
называется
сходящимся абсолютно, если сходится
ряд из модулей 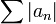 ,
иначе — сходящимся условно.
,
иначе — сходящимся условно.Аналогично, если несобственный интеграл
 от
функции сходится, то он называется
сходящимся абсолютно или условно в
зависимости от того, сходится или нет
интеграл от ее модуля
от
функции сходится, то он называется
сходящимся абсолютно или условно в
зависимости от того, сходится или нет
интеграл от ее модуля 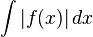 .
.В случае общего нормированного пространства модуль в определении заменяется на норму.
Несобственный
интеграл первого рода  называется абсолютно
сходящимся,
если сходится интеграл
называется абсолютно
сходящимся,
если сходится интеграл 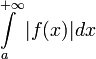 .
.
Свойства
из сходимости интеграла
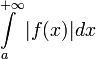 вытекает
сходимость интеграла
вытекает
сходимость интеграла  .
.Для выявления абсолютной сходимости несобственного интеграла первого рода используют признаки сходимости несобственных интегралов первого рода от неотрицательных функций.
Если интеграл
 расходится,
то для выявления условной
сходимости несобственного
интеграла первого рода могут быть
использованы признаки Абеля и Дирихле.
расходится,
то для выявления условной
сходимости несобственного
интеграла первого рода могут быть
использованы признаки Абеля и Дирихле.
Признак Абеля: Признак Абеля дает достаточные условия сходимости несобственного интеграла.
Признак
Абеля для несобственного
интеграла I-рода (для бесконечного промежутка).
Пусть функции ![]() и
и ![]() определены
на промежутке
определены
на промежутке ![]() .
Тогда несобственный интеграл
.
Тогда несобственный интеграл 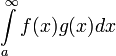 сходится,
если выполнены следующие условия:
сходится,
если выполнены следующие условия:
Функция
 интегрируема
на
интегрируема
на  .
.Функция
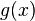 ограничена
и монотонна.
ограничена
и монотонна.
Признак
Абеля для несобственного интеграла II-рода (для
функций с конечным числом разрывов).
Пусть функции ![]() и
и ![]() определены
на промежутке
определены
на промежутке ![]() .
Тогда несобственный интеграл
.
Тогда несобственный интеграл  сходится
если выполнены следующие условия:
сходится
если выполнены следующие условия:
Функция
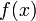 интегрируема
на
интегрируема
на  т.е.
сходится интеграл
т.е.
сходится интеграл 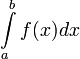
Функция
 ограничена
и монотонна на
ограничена
и монотонна на  .
.
Признак Дирихле: Признак Дирихле — теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна-Дирихле.
|
Пусть выполнены условия:
Тогда |
Очевидно, что вместо второго условия можно также записать
 .
.Условие монотонности в признаке Дирихле существенно.
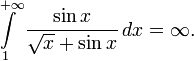
Однако, условие монотонности не является необходимым.
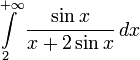 —
сходится.
—
сходится.
Условие ограниченности первообразной в признаке Дирихле также является существенным, но не является необходимым.
Условная сходимость: Ряд
 называетсяусловно сходящимся,
если сам он сходится, а ряд, составленный
из абсолютных
величин его
членов, расходится. То есть, если
называетсяусловно сходящимся,
если сам он сходится, а ряд, составленный
из абсолютных
величин его
членов, расходится. То есть, если 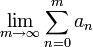 существует
(и не бесконечен), но
существует
(и не бесконечен), но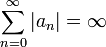 .
.Если ряд условно сходится, то ряды, составленные из его положительных и отрицательных членов, расходятся.
Путём изменения порядка членов условно сходящегося ряда можно получить ряд, сходящийся к любой наперёд заданной сумме или же расходящийся (теорема Римана).
При почленном умножении двух условно сходящихся рядов может получиться расходящийся ряд.
47 Вопрос:
Если функция не ограничена на промежутке интегрирования и промежуток интегрирования конечен, то определенный интеграл является несобственным интегралом второго рода.
1. Пусть функция y = f(x) определена и непрерывна на [a,b) и в точке b функция не ограничена.
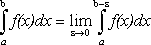 .
.
Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и равен значению этого предела, в противном случае интеграл называется расходящимся.
Если оба предела, стоящие в правой части, существуют и конечны, то несобственный интеграл называется сходящимся и он равен сумме этих пределов, в противном случае – расходящимся.
Замечание 1. Несобственные интегралы могут быть комбинированного типа: первого и второго рода; или второго рода с несколькими точками разрыва второго рода.
Замечание 2. Если функция на отрезке интегрирования терпит разрыв первого рода в точке с, то определенный интеграл от нее по этому отрезку не является несобственным, т.е. его можно свести к сумме двух обычных определенных интегралов.
 .
.

 сходится.
сходится.