41 Вопрос:

 Площадь криволинейной трапеции

     Криволинейной трапецией называется фигура, ограниченная графиком заданной на сегменте [a, b] непрерывной и неотрицательной фукнции f(x), ординатами, проведенными в точках a и b, и отрезком оси Ox между точками a и b (см. Рис. 2).

     Докажем следующее утверждение.

     Криволинейная трапеция представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле

     (1)

     Доказательство. Так как непрерывная на сегменте [a, b] функция интегрируема, то для любого положительного числа ε можно указать такое разбиение Tсегмента [a, b], что разность S - s < ε, где S и s - соответственно верхняя и нижняя суммы разбиения T. Но S и s равны соответственно S_d и S_i, где S_d и S_i - площади ступенчатых фигур (многоугольников), первая из которых содержит криволинейную трапецию, а вторая содержится в криволинейной трапеции (на Рис. 2 изображены также и указанные ступенчатые фигуры). Так как S_d - S_i < ε, то, в силу теоремы 1, криволинейная трапеция квадрируема. Поскольку предел при Δ → 0 верхних и нижних сумм равен и s ≤ P ≤ S, то площадь P криволинейной трапеции может быть найдена по формуле (1).

     Замечание. Если функция f(x) непрерывна и неположительна на сегменте [a, b], то значение интеграла равно взятой с отрицательным знаком площади криволинейной трапеции, ограниченной графиком функции f(x), ординатами в точках a и b и отрезком оси Ox между точками a и b. Поэтому, еслиf(x) меняет знак, то равен сумме взятых с определенным знаком площадей криволинейных трапеций, расположенных выше и ниже оси Ox, причем площади первых берутся со знаком +, а вторых со знаком -.

Площадь криволинейного сектора

     Пусть кривая L задана в полярной системе координат уравнением r = r(θ), α ≤ θ ≤ β (см. Рис. 3), причем функция r(θ) непрерывна и неотрицательна на сегменте [α, β]. Плоскую фигуру, ограниченную кривой L и двумя лучами, составляющими с полярной осью углы α и β, будем называть криволинейным сектором.

     Докажем следующее утверждение. Криволинейный сектор представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле

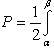
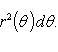     (2)

     Доказательство. Рассмотрим разбиение T сегмента [α, β] точками α = θ₀ < θ₁ < ... < θ_n = β и для каждого частичного сегмента [θ_i-1, θ_i] построим круговые секторы, радиусы которых равны минимальному r_i и максимальному R_i значениям r(θ) на сегменте [θ_i-1, θ_i]. В результате получим две веерообразные фигуры, первая из которых содержится в криволинейном секторе, а вторая содержит криволинейный сектор (эти веерообразные фигуры изображены на Рис. 3). Площади и указанных веерообразных фигур равны соответственно и . Отметим, что первая из этих сумм является нижней суммойs для функции для указанного разбиения T сегмента [α, β], а вторая сумма является верхней суммой S для этой же функции и этого же разбиения. Так как функция интегрируема на сегменте [α, β], то разность может быть как угодно малой. Например, для любого фиксированного ε > 0 эта разность может быть сделана меньше ε/2. Впишем теперь во внутреннюю веерообразную фигуру многоугольник Q_i с площадью S_i, для которого , и опишем вокруг внешней веерообразной фигуры многоугольник Q_d площадью S_d, для которого ^*. Очевидно, первый из этих многоугольников вписан в криволинейный сектор, а второй описан вокруг него. Так как справедливы неравенства

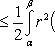
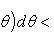
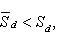     (3)

то, очевидно, S_d - S_i < ε. В силу произвольности ε, отсюда вытекает квадрируемость криволинейного сектора. Из неравенств (3) вытекает справедливость формулы (2).