2. Перевірка відповідності розподілу випадкового компонента нормальному закону розподілу

Може бути зроблена лише приблизно за допомогою дослідження показників асиметрії ()і ексцесу (),тому що тимчасові ряди, як правило, не дуже великі. При нормальному розподілі показники асиметрії й ексцесу деякої генеральної сукупності дорівнюють нулю. Ми припускаємо, що відхилення від тренда являють собою вибірку з генеральної сукупності, тому можна визначити тільки вибіркові характеристики асиметрії й ексцесу і їхньої помилки:

;
;
;
;

−вибірна характеристика асиметрії, ексцесу;

−середньоквадратичні помилки.

Якщо одночасно виконуються наступні нерівності:

то гіпотеза о нормальнім характері розподілу випадкової компоненти приймається.

Якщо виконується хоча б одне з нерівностей:

то гіпотеза відкидається та модель вважається неадекватною.

3. Перевірка рівності математичного очікування випадкового компонента нулю

Якщо вона розподілена за нормальним законом, здійснюється на основі t-критерію Стьюдента. Розрахункове значення цього критерію задається формулою:

Якщо розрахункове значення t менше табличного значення t_а статистики Стьюдента із заданим рівнем значимості а й числом ступенів волі n-1, то гіпотеза про рівність нулю математичного очікування випадкової послідовності приймається; у противному випадку ця гіпотеза відкидається й модель уважається неадекватною.

5.8.4. Перевірка незалежності значень рівнів випадкового компонента.

Т.ч. перевірка відсутності істотної автокореляції в залишковій послідовності може здійснюватися по ряду критеріїв, найпоширенішим з яких є d- критерій Дарбина-Уотсона. Розрахункове значення цього критерію визначається по формулі:

Помітимо, що розрахункове значення критерію Дарбина- Уотсона в інтервалі від 2 до 4 свідчить про негативний зв'язок; у цьому випадку його треба перетворити по формулі d' = 4 - d і в подальшому використовувати значення d'.

Розрахункове значення критерію d (або d') рівняється з верхнім d₂ і нижнім d₁ критичними значеннями статистики Дарбина-Уотсона, фрагмент табличних значень яких для різного числа рівнів ряду п і числа обумовлених параметрів моделі.

Таблица

d-критерий Дарбина-Уотсона

n	k=1		k=2		k=3
	d1	d2	d1	d2	d1	d2
15 20 30	1,08 1,20 1,35	1,36 1.41 1,49	0,95 1,10 1,28	1,54 1,54 1,57	0,82 1,00 1,21	1,75 1,68 1,65

Висновок про адекватність трендової моделі робиться, якщо всі зазначені вище чотири перевірки властивостей залишкової послідовності дають позитивний результат. Для адекватних моделей має сенс ставити завдання оцінки їхньої точності. Точність моделі характеризується величиною відхилення виходу моделі від реального значення моделюючої змінної (показника). Для показника, представленого часовим рядом, точність визначається як різниця між значенням фактичного рівня тимчасового ряду і його оцінкою, отриманої розрахунковим шляхом з використанням моделі, при цьому як статистичні показники точності застосовуються наступні:

Середнє квадратичне відхилення:

Середня відносна помилка апроксимації:

Коефіцієнт збіжності:

Коефіцієнт детермінації:
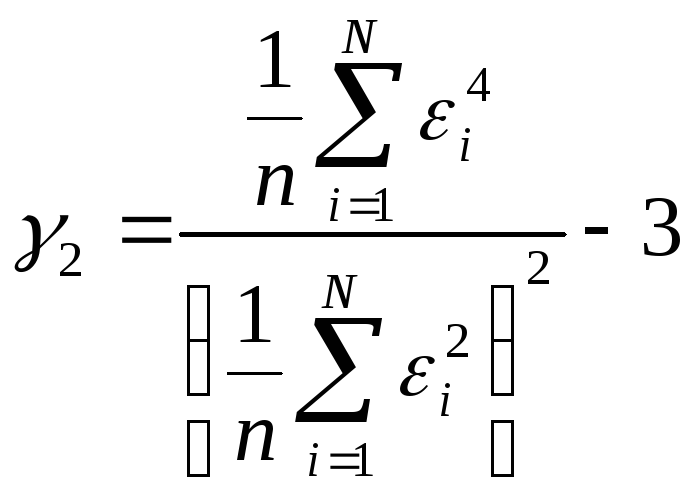