
- •Міністерство освіти і науки україни
- •Матриці і операції над ними. Визначники матриць. Властивості визначників. Обернена матриця.
- •Зразки розв’язування задач.
- •Зразки розв’язування задач.
- •Розв’язати системи рівнянь за формулами Крамера:
- •Дослідити на сумісність системи лінійних рівнянь та знайти їх розв’язок у випадку сумісності:
- •Розв’язати систему лінійних рівнянь матричним методом:
- •Завдання для самостійної роботи.
- •3.Вектори в просторі. Основні поняття. Лінійні операції з векторами. Прямокутна система координат у просторі.
- •Довжину вектора будемо позначати таким чином:
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •4. Скалярний, векторний, мішаний добутки векторів. Застосування в задачах геометрії. Умови перпендикулярності та компланарності векторів.
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •5.Загальне і канонічне рівняння прямої. Рівняння прямої у відрізках на осях. Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, яка проходить через дві дані точки. Перетин двох прямих.
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •6. Кут між двома прямими. Пучок прямих, які проходять через дану точку. Нормальне рівняння прямої. Відстань від точки до прямої.
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •7. Криві другого порядку: коло, еліпс.
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •8. Криві другого порядку: гіпербола, парабола.
- •I. Гіпербола
- •II.Парабола
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •9. Рівняння площини в просторі.
- •Зразки розв’язування задач.
- •Завдання для самостійної роботи.
- •10. Пряма в просторі. Площина і пряма.
- •Зразки розв’язування задач
- •Завдання для самостійної роботи.
- •11. Нескінченна числова послідовність. Границя числової послідовності і її властивості. Нескінченно малі і нескінченно великі послідовності.
- •12. Похідна функції. Похідні основних елементарних функцій. Основні правила диференціювання.
- •Зразки розв’язування задач
- •Завдання для самостійної роботи.
- •Література
Зразки розв’язування задач.
Розв’язати системи рівнянь за формулами Крамера:


Розв’язання:
Заходимо визначник системи
![]() ,
тому система має єдиний розв’язок .
Знаходимо
,
тому система має єдиний розв’язок .
Знаходимо
![]()
![]() .
.
За формулами Крамера , маємо:
![]()
б) Знаходимо визначник системи:

Система
має єдиний розв’язок. Знаходимо
![]()

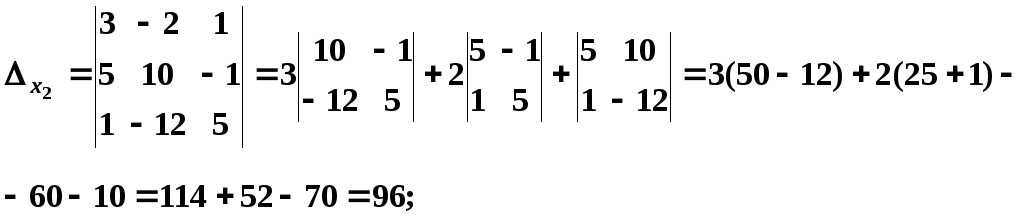

За формулами Крамера, маємо:
![]()
Дослідити на сумісність системи лінійних рівнянь та знайти їх розв’язок у випадку сумісності:
а)
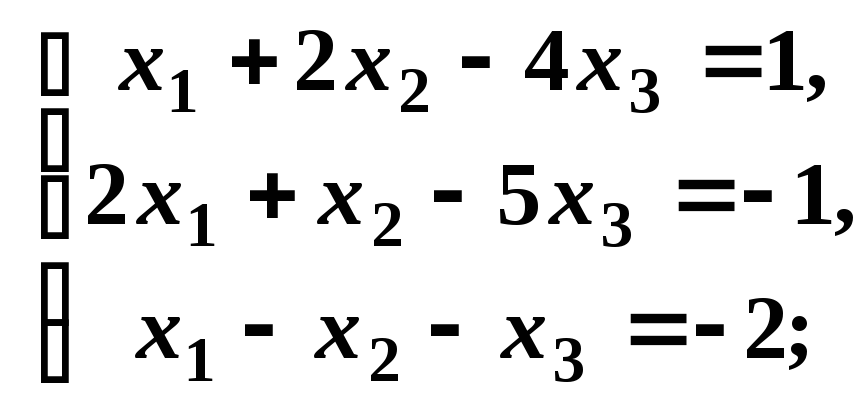 б)
б)
Розв’язання:
Обчислемо визначник системи:

Визначник
системи дорівнює нулю. Система або має
безліч розв’язків, або не має жодного
розв’язку. Знаходимо
![]()
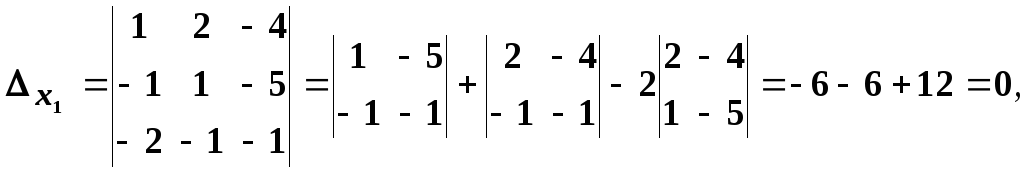


Оскільки,
![]() ,
то система сумісна і невизначена. Для
знаходження всіх розв’язків, відкидаємо
третє рівняння, а рівняння , що залишилися,
записуємо у вигляді:
,
то система сумісна і невизначена. Для
знаходження всіх розв’язків, відкидаємо
третє рівняння, а рівняння , що залишилися,
записуємо у вигляді:
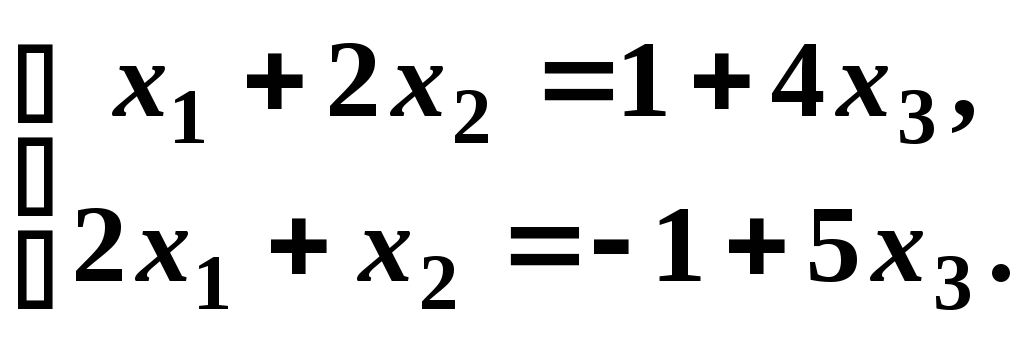
Розв’язуємо отриману систему за формулами Крамера:
![]()
![]()
![]() ;
;
![]()
б)
 ,
тому що другий і третій рядки пропорційні.
,
тому що другий і третій рядки пропорційні.
Система або має безліч розв’язків, або не має жодного розв’язку.
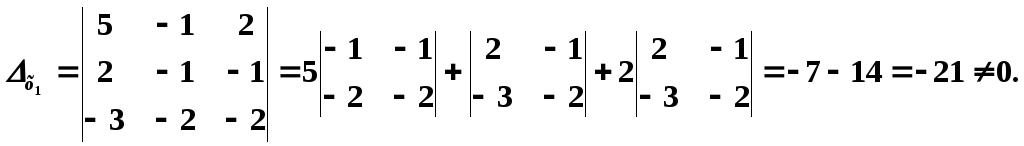
Отже, задана система не має жодного розв’язку, тобто вона є несумісною.
Розв’язати систему лінійних рівнянь матричним методом:

Розв’язання:
Запишемо
дану систему рівнянь у матричній формі:
![]() де
де

 значить
матриця А
має обернену матрицю.
значить
матриця А
має обернену матрицю.
Знайдемо алгебричні доповнення елементів матриці А :


Скориставшись
рівністю
![]() ,
знаходимо розв’язок
системи:
,
знаходимо розв’язок
системи:

![]() -
шуканий розв’язок.
-
шуканий розв’язок.
Завдання для самостійної роботи.
Розв’язати системи лінійних рівнянь за формулами Крамера:
а)
 б)
б)
Визначити, при яких значеннях а і b система
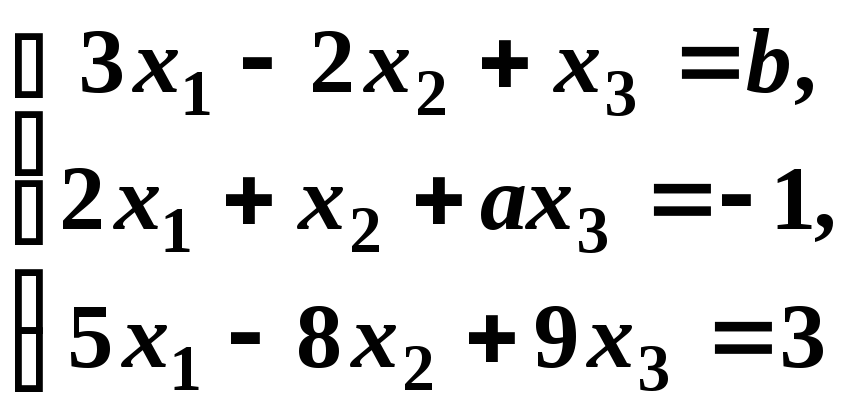
а) має один розв’язок;
б) має безліч розв’язків;
в) не має жодного розв’язку.
Розв’язати системи лінійних рівнянь матричним методом:
а)
 б)
б)
3.Вектори в просторі. Основні поняття. Лінійні операції з векторами. Прямокутна система координат у просторі.
Розглянемо
напрямлений відрізок
![]() ,
деА
– початок, В
– кінець.
Будемо називати його вектором.
,
деА
– початок, В
– кінець.
Будемо називати його вектором.
Довжину вектора будемо позначати таким чином:
![]() .
.
Додавання векторів.
Щ
Рис.
3.1
![]() і
і![]() ,
треба відкласти ці вектори від довільної
точки та побудувати на них паралелограм.
Сумою векторів буде діагональ, що
виходить з початку векторів
,
треба відкласти ці вектори від довільної
точки та побудувати на них паралелограм.
Сумою векторів буде діагональ, що
виходить з початку векторів![]() і
і![]() (рис. 3.1).
(рис. 3.1).
Цей спосіб побудови називається правилом паралелограма.
Суму двох векторів можно побудувати ще й за правилом трикутника.
В
Рис.
3.2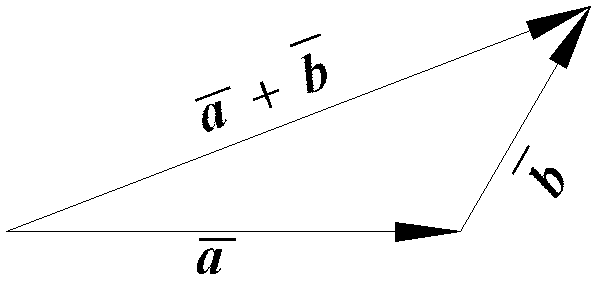
![]() від кінця вектора
від кінця вектора![]() .
Сумою векторів
.
Сумою векторів![]() і
і![]() буде вектор, що з’єднує початок
буде вектор, що з’єднує початок![]() з кінцем
з кінцем![]() (рис. 3.2).
(рис. 3.2).
Щ
Рис.
3.3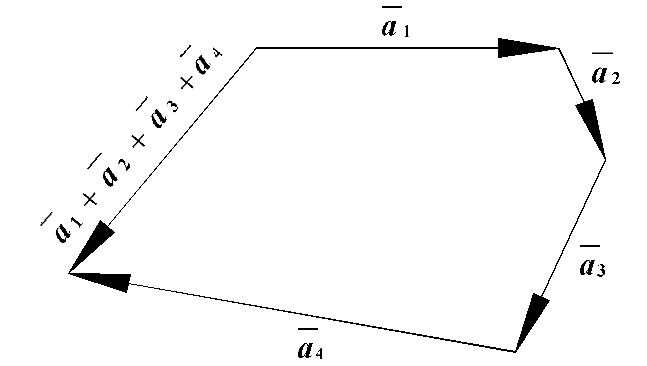
![]() ,
треба від довільної точки відкласти
,
треба від довільної точки відкласти![]() ,
потім від його кінця відкласти
,
потім від його кінця відкласти![]() і т.д., нарешті від кінця
і т.д., нарешті від кінця![]() відкласти
відкласти![]() .
Сумою векторів буде вектор, напрямлений
від початку
.
Сумою векторів буде вектор, напрямлений
від початку![]() до кінця
до кінця![]() (рис. 3.3).
(рис. 3.3).
Віднімання векоторів.
Щ
Рис.
3.4
![]() ,
треба відкласти ці вектори від довільної
точки, з’єднати їх кінці та вибрати на
цьому відрізку напрямок від кінця
,
треба відкласти ці вектори від довільної
точки, з’єднати їх кінці та вибрати на
цьому відрізку напрямок від кінця![]() до кінця
до кінця![]() (рис. 3.4).
(рис. 3.4).
Множення вектора на число.
Добутком
ненульового вектора
![]() на числоk
називається вектор, який має напрям
вектора
на числоk
називається вектор, який має напрям
вектора
![]() ,
якщо
,
якщо![]() ,
і протинапрям, якщо
,
і протинапрям, якщо![]() (при
(при
![]() ,
,![]() ).
).
Ці три операції називаються лінійними операціями з векторами.
Проекція вектора на вісь.
П
Рис.
3.5
![]() ,
,
![]() .
.
Властивості проекції.
 ;
;
б)
![]() ;
;
в)
![]() .
.
Прямокутна система координат.
Нехай
у просторі задано три попарно
перпендикулярні осі OX,
OY, OZ. Координатами
вектора
![]() на осі
називаються проекції вектора на ці осі:
на осі
називаються проекції вектора на ці осі:
![]() ,
,
![]() ,
,![]() .
.
Якщо
![]() -
одиничні вектори, що напрямлені поOX,
OY, OZ, то
-
одиничні вектори, що напрямлені поOX,
OY, OZ, то
![]() .
.
Якщо
![]() ,
,![]() то координати вектора
то координати вектора
![]() .
.
Правила дій над векторами, заданими своїми координатами.
Якщо
![]() ,
,![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() .
.
Довжина вектора. Напрямлені косинуси вектора.
![]() ;
;
![]() ;
; ![]() ;
;![]() ,
,
де
![]() -
кути між
-
кути між![]() та осямиOX,
OY, OZ.
та осямиOX,
OY, OZ.
Для напрямлених конусів справедливо співвідношення:
![]()
Поділ відрізка в даному відношенні.
Нехай
точки А,
В
мають координати
![]() ,
,![]() .
.
Якщо
відрізок АВ
поділимо точкою М
у відношенні:
![]() ,
то координати точкиМ
знаходять за формулами:
,
то координати точкиМ
знаходять за формулами:
![]() ;
; ![]()
![]() .
.
Якщо
![]() ,
то отримуємо формули для знаходження
координат середини відрізка.
,
то отримуємо формули для знаходження
координат середини відрізка.
