1.12.4. Осьові моменти опору.

Осьовим моментом опору називають відношення моменту інерції відносно даної осі до відстані до найбільш віддаленої точки перерізу:

W_x= І_х /у_max , W_y = І_у /х_{max ,} [м³].

1.12.5. Геометричні характеристики простих фігур.

Допустимо балка має прямокутний переріз (рис.1.12.2.).

Т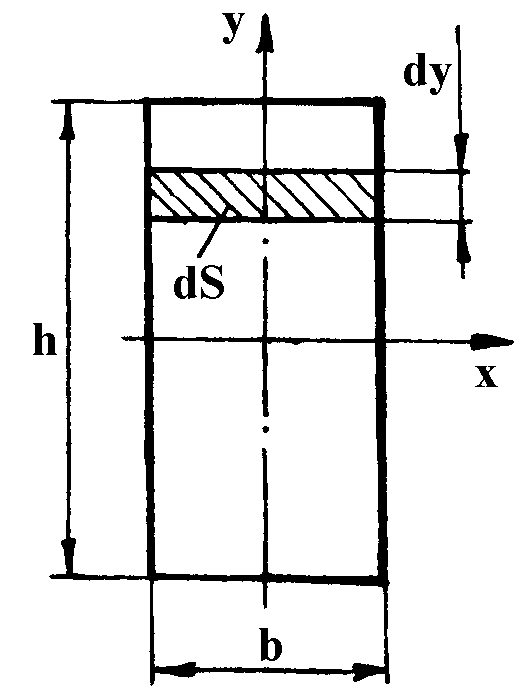оді осьовий момент інерції буде дорівнювати:

І_х = =²dy = 2b²dy =

= │ = 2b · (h/2)³ / 3 = bh³ / 12 .

Аналогично:

І_y = hb³ / 12 .

Осьовий момент опору для прямокутного перерізу:

.

Рис.12.2.Розрахункова схема.

Осьовий момент опору для прямокутного перерізу:

.

Аналогічно:

.

Провівши аналогічні розрахунки для круглого поперечного перерізу отримаємо:

- осові моменти інерції:

І_x = І_y = d ⁴ / 64 , де d – діаметр круглого перерізу;.

- полярний момент інерції:

І_p = І_x + І_y = d ⁴ /32;

- осьові моменти опору:

W_x = W_y = І_x/(d/2) = d ³ /32;

- полярний момент опору:

W_P = І_p/(d/2) = d ³ /16 .

Моменти опору прокатних профілів (кутників, швелерів, двутаврів) наводяться в спеціальних довідкових таблицях.

1.13. Види навантажень та види деформацій

Прикладені до тіла зовнішні сили викликають різні внутрішні зусилля в поперечних перерізах цього тіла. В результаті тіло деформується. Існує п’ять видів навантажень (а також п’ять видів деформацій з такими ж назвами):

1. Розтяг - в поперечних перерізах тіла діє тільки подовжня сила N, що спрямована від перерізу. Стиск - сила N спрямована до перерізу.

2. Зсув (зріз) - в поперечних перерізах тіла діє тільки поперечна сила Q_x або Q_y.

3. Кручення - в поперечних перерізах тіла діє тільки крутний момент Т.

4. Згин - в поперечних перерізах тіла діє тільки згинаючий момент M_x або M_y.

5. Складна деформація - в поперечних перерізах тіла діє декілька зусиль (наприклад згинаючий і крутний моменти).

1.14. Напруження

1.14.1. Повнe напруження та його складові.

Напруження – це інтенсивність внутрішніх сил пружності. Напруження визначається як внутрішня сила пружності, що приходиться на одиницю площі в даній точці даного перерізу.

Розглянемо в деформуємому тілі довільний переріз з нормаллю n (рис.1.14.1).

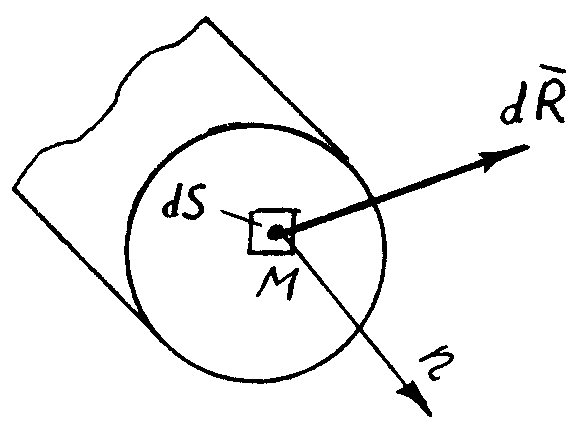
Рис.1.14.1. Повне напруження в довільній точці.

Виділимо біля точки М малу площадку dS. Допустимо, рівнодіюча сил пружності на цій площадці дорівнює dR. Тоді повне напруження в точці М визначається за формулою:

p = dR/dS [Н/м²].

Повне напруження p можна розкласти на дві складові:

• нормальну до площини перерізу, що називається нормальним напруженням і позначається буквою ;

• складову, що лежить в площині перерізу, – дотичне напруження (). Дотичне напруження також можна представити у вигляді двох складових за напрямками осей координат (рис.1.14.2).

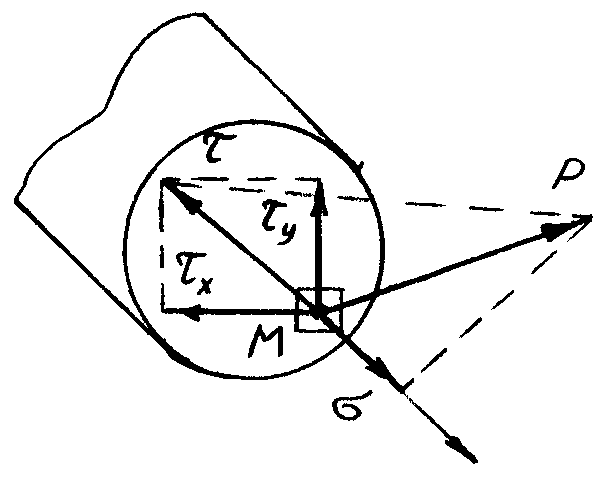
Рис.1.14..2. Складові повного напруження.

Вказані напруження визначаються за формулами:

 = dN / dS; _x = dQ_x / dS;_y = dQ_y / dS.