1.18.6. Розрахунки на міцність при складній деформації.

Складна деформація – це вид деформації, при якому в поперечних перерізах бруса одночасно виникає не менше двох внутрішніх факторів. До складних деформацій відносяться: вигин з розтягом - стиском; вигин з крученням; кручення з розтягом - стиском. Прямий поперечний вигин не вважається складною деформацією, оскільки впливом поперечної сили в інженерних розрахунках нехтують.

У випадку вигину з розтягом - стиском діють одночасно подовжні і поперечні сили. У цьому випадку нормальне напруження в будь-якій точці перерізу визначається як алгебраїчна сума напружень від вигину і розтягу - стиску: _max = N / S + M_y /W_y + M_x /W_{x .}

Аналогічно визначаються напруження при нецентровому розтязі - стиску, тобто коли брус знаходиться під дією подовжніх сил, рівнодіюча яких не співпадає з віссю бруса, а також при косому вигині, тобто такому вигині, при якому площина згинаючого момента не співпадає з жодною з головних площин інерції бруса.

Приспільнійдіївигинуікручення абокрученняірозтягу- стискурозрахунковіформулиотримуютьнапідставіспеціальнихтеорійміцності.При цьому розраховують еквівалентні напруження і порівнюють їх з допустимими.

Так, наприклад, за теорією найбільших дотичних напружень еквівалентне напруження визначають за формулою:

_ек. = _х² + 4_х²  [] ,

а за енергетичною теорією міцності:

_ек. = _х² + 3_х²  [] .

1.19. Основи теорії деформованого стану

1.19.1. Загальні визначення.

Усі реальні тіла під дією зовнішніх навантажень деформуються, тобто змінюють свою форму і розміри. Деформований стан навантаженого тіла характеризується лінійними і кутовими деформаціями.

Представимо тіло з розмірами dx, dy, dz, на гранях якого діють напруження.

Під дією напружень тіло деформується. Деформація полягає в зміні довжини його ребер на величину dy, dz, dx (рис.1.19.1.) і в зміні кутів між його гранями на величину _xy, _yz, _xz (рис.1.19.2.).

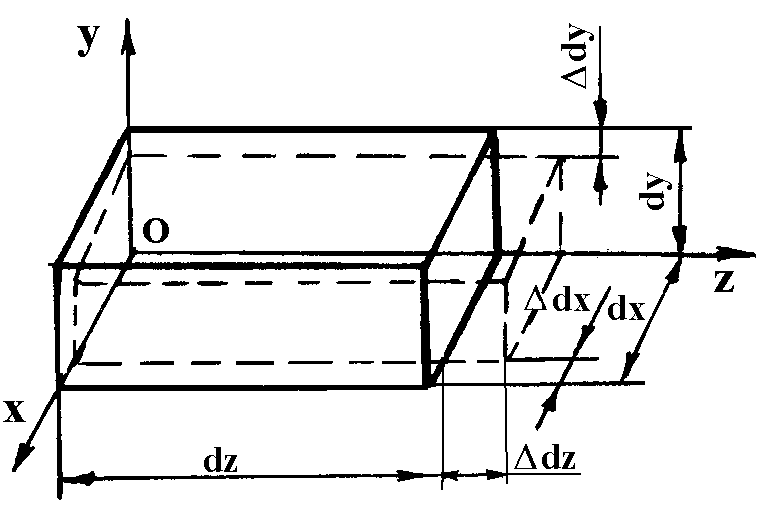
Рис. 1.19.1. Подовжній розтяг тіла.

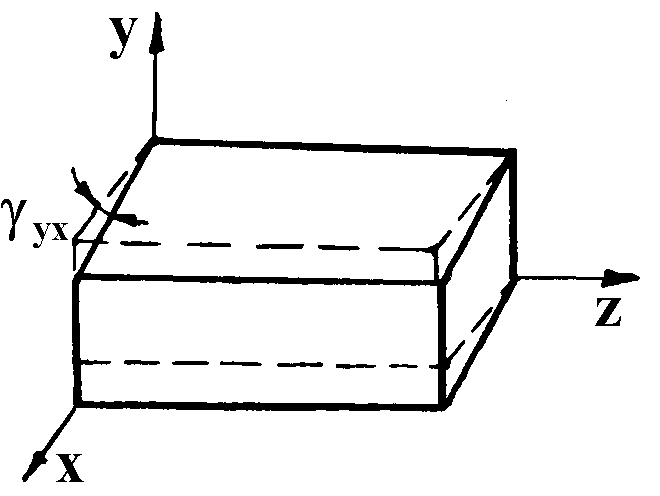
Рис.1.19.2. Поперечний зсув граней тіла.

Величини dx, dy, dz називають абсолютними подовженнями (укороченнями). Вони являють собою різницю між довжиною відповідного ребра тіла до і після деформації.

Абсолютне подовження, що приходиться на одиницю первісної довжини, називається відносним.

_x = ; _y = ; _z = .

Відносні подовження (укорочення) тіла називаються лінійними деформаціями. Величини _xy,_yz,_xz називаються кутами зсуву або кутовими деформаціями. Лінійні деформації () пов’язані з дією нормальних напружень (), а кутові деформації () пов’язані з дією дотичних напружень ().

1.19.2. Закон Гука. Коефіцієнт Пуассона.

Закон Гука встановлює залежність між напруженнями та деформаціями: деформація прямо пропорційна напруженню. Це можна виразити формулами:

 = E ·  ,  = G ·  ,

де  - нормальне напруження, мПа;

 - дотичне напруження, мПа;

 - лінійна деформація;

 - кутова деформація;

E – модуль пружності материала при розтязі, мПа, (для сталі

E = 2·10⁵ мПа);

G – модуль пружності матеріала при зсуві, мПа.

При розтязі (стиску) виникають подовжня () та поперечна (’) деформації (  = ; ’ = ), між якими існує залежність:

’ = – ·,

де  - коефіцієнт Пуассона, що характеризує здатність матеріала до поперечних деформацій (0  0,5).