2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних

Рівняння дотичної площини і нормалі до поверхні в даній її точцімають вигляд:

; (2.9)

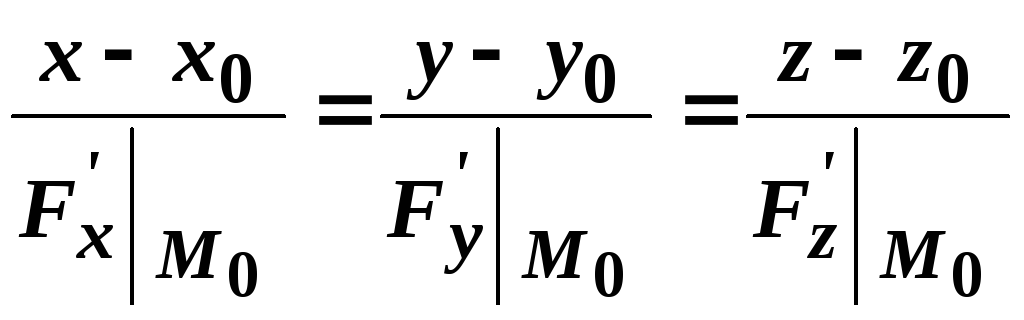. (2.10)

Нехай функція визначена в деякому околі точки. Точканазиваєтьсяточкою максимуму (мінімуму) функції , якщо знайдеться такій окіл точки, в якому для будь-якої точкивиконується нерівність:. Максимуми і мінімуми функції називаються їїекстремумами, а точки, в яких досягаються екстремуми - точками екстремуму.

Необхідна умова існування екстремуму.

Якщо диференційована функція має в точціекстремум, то в цій точці виконуються рівності:

, .(2.11)

Точки, в яких виконуються рівності (2.11), називаються точками можливого екстремуму або стаціонарними.

Достатня умова існування екстремуму функції.

Нехай у точці можливого екстремуму і деякому її околі функціямає неперервні частинні похідні другого порядку. Позначимоі покладемо. Тоді:

а) якщо , то- точка екстремуму, причому при- точка максимуму, при- мінімуму;

б) якщо , то в точціекстремуму немає;

в) у випадку , функціяу стаціонарній точціможе мати екстремум або ні.

Зразки розв’язування задач

1. Скласти рівняння дотичної площини і нормалі до поверхні у точці:

а)у точці.

Знайдемо :. Отже,.

Позначимо .Тоді частинні похідні:

, ,.

Обчислимо значення частинних похідних в точці :

,

,

.

Згідно з формулою (2.9), рівняння дотичної площини має вигляд:

,

або .

За формулою (2.10) складемо рівняння нормалі:

.

б) у точці.

Знайдемо ,,.

Значення частинних похідних в точці :

,

,

.

Складемо рівняння дотичної площини:

,

або .

Рівняння нормалі:

або .

2. Дослідити функції на екстремум:

а) .

Обчислимо частинні похідні функції: ,.

Знайдемо стаціонарні точки. Для цього розв’яжемо систему рівнянь:

або

Визначаючи з першого рівняння і підставляючи його виразу

друге, маємо: , звідки,. Тоді,.

Отже, точки і- стаціонарні. Обчислимо частинні похідні другого порядку даної функції:,,.

Знайдемо їх значення в стаціонарних точках:

, ,;

, ,.

Враховуємо, що , отже, в точці

екстремуму немає. Обчислимо та, а тому в точцідана функція має мінімум, причому.

б) .

Частинні похідні першого порядку: та. Знайдемо

стаціонарні точки:

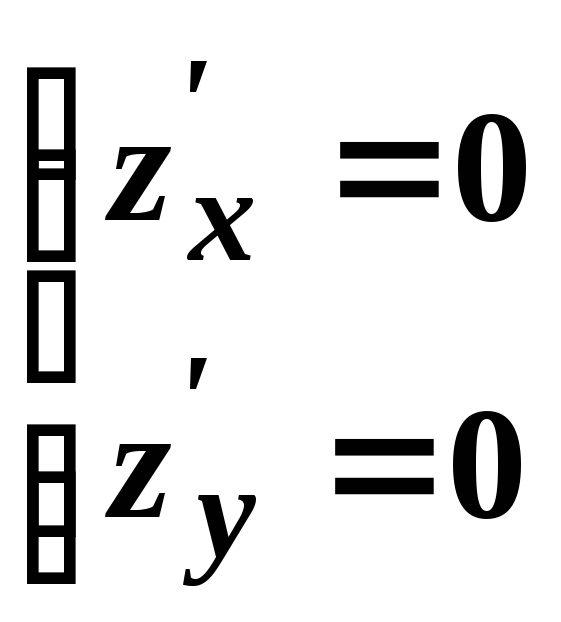
, звідки

Отже, точка є стаціонарною. Частинні похідні другого порядку:

, ,.

Тоді ,,. Обчислимо.

Отже, в точці є екстремум. Так як, то в точціфункція має мінімум:

.

Завдання для самостійної роботи

1. Скласти рівняння дотичної площини і нормалі до поверхні у заданій точці:

а) ,;

б) ,;

в) ,.

2. Дослідити функції на екстремум:

а) ; б).