1.5.2 Расчет опорного подшипника скольжения с самоустанавливающимися подушками.

1.5.2.1 Методика расчета

При расчете опорных подшипников, основываясь на результатах ранее проведенных исследований, как и для упорных подшипников было принято, что температура смазочного слоя по толщине постоянна, градиент температуры по ширине подушки мал по сравнению с угловым градиентом, а все выделяемое тепло отводится смазкой.

Математическая модель, описывающая неизотермическое течение смазки в опорном подшипнике, состоит из уравнений Рейнольдса и энергии, которые в безразмерной форме имеют следующий вид:

; (4.2.1)

; (4.2.2)

где ;

= /₁ ; _n ; z2zB;

h=h_i /h_Po ; P=Ph_Po² /₁R²_n ;

t =c₁₁h_Po²(t-t₁) /₁R²_n ;

h_i - толщина смазочного слоя в рассматриваемой точке i-той подушки;

t,  - температура и коэффициент динамической вязкости смазки в рассматриваемой точке;

с₁, ₁ - теплоемкость и плотность смазки при температуре t₁;

t₁, ₁ - температура и коэффициент динамической вязкости смазки на входе в смазочный слой;

R - радиус шейки вала;

Р - гидродинамическое давление;

• - угловая скорость вращения ротора;

h_Po - радиальный зазор под точкой опоры подушки при центральном положении шейки вала (е=0); i=1…z_n;

z_n - число подушек.

Эти уравнения описывают соответственно распределение давления и температуры в смазочном слое.

Форма смазочного слоя i-той подушки зависит от взаимного положения подушки и шейки вала, характеризуемого смещением шейки вала от центра подшипника, углом поворота подушки, кривизной рабочей поверхности подушки и описывается следующим выражением:

h_i =h_i /h_Po =1- cos[_ni-_e+ _n (_p-)]+m₀_n²(_p-)²/[2(1-m₀)]+ +(1+H_ni_n (_p-), (4.2.3)

где  =е /hp₀ ; m₀=1-h_Po/; =R_n-R; _p=_P/_n;

H=H/R; _ni=_ni /; =h_Po/R;

е - смещение шейки вала;

R_n - радиус рабочей поверхности подушки;

_P - координата расположения точки опоры подушки;

Н - высота подушки;

_ni - угол поворота i-той подушки;

_ni - угол расположения i-ой подушки;

_е - угол эксцентриситета.

Зависимость вязкости смазки от температуры аппроксимирована выражением

=ехр[-(t-t₁)], (4.2.4)

где (4.2.5)

 - коэффициент, учитывающий степень изменения вязкости в рассматриваемом диапазоне температур

от t₁ до t_к,

t_к , _к - температура и коэффициент динамической вязкости смазки в конце рассматриваемого диапазона температур.

Угол поворота _ni самоустанавливающейся подушки находится из условия равновесия, когда сумма опрокидывающих моментов относительно ребра качания равна нулю:

. (4.2.6)

Величина угла эксцентриситета _е находится из условия равновесия шейки

вала, при котором сумма горизонтальных составляющих гидродинамических реакций в смазочных слоях всех подушек равна нулю:

. (4.2.7)

Проведенные экспериментальные исследования показали , что в опорных подшипниках скольжения с самоустанавливающимися подушками центробежных компрессоров кривая подвижного равновесия практически совпадает с линией действия нагрузки. Этот факт позволяет при разработке методики и программы расчета принять угол эксцентриситета _е равным нулю.

Граничными условиями для приведенной системы уравнений являются:

Р_г =0 (давление по наружному контуру подушки Г равно нулю) и t=0 при =0 (температура смазки на входе в смазочный слой полагается известной).

Результаты решения данной задачи обобщены в виде зависимостей безразмерных коэффициентов несущей способности, потерь мощности на трение в смазочном слое  , максимальной температуры t_max и минимальной толщины h_min смазочного слоя единичной подушки от режимного параметра

(4.2.8)

и относительного эксцентриситета  для различных значений степени нереверсивности подушек _р.

Проведенные экспериментальные исследования показали, что температура смазки на входе в смазочный слой t₁ близка к температуре смазки на сливе из подшипника t₂. Этот факт позволяет определять температуру t₁ из условия теплового баланса

t₁ ~ t₂=t₀+ , (4.2.9)

где t₀ - температура смазки на входе в подшипник,

N, Q - суммарные потери мощности на трение в подшипнике и расход смазки через подшипник.

Таким образом, инженерный метод расчета подшипника может сводиться:

а) к вычислению гидродинамической реакции подшипника, потерь мощности на трение, максимальной температуры смазочного слоя и расхода смазки через подшипник для заданного значения (ряда значений) относительного эксцентриситета и оценки ограничивающих параметров, какими являются максимальная температура и минимальная толщина смазочного слоя;

б) к определению взаимного положения подушек и шейки вала, вычислению максимальной температуры, минимальной толщины смазочного слоя, потерь мощности на трение и расхода смазки через подшипник для заданного значения нагрузки.

Исходные данные для расчета подшипника представлены в таблице 5.

Выполнение различных вариантов расчета обеспечивается вводом соответствующих значений признаков расчета PRS, PRF, PRZ, PRT,PRР.

Расчет подшипника ведется в следующей последовательности:

- задаются предварительное значение перепада температуры смазки в подшипнике t и температура смазки в конце рассматриваемого диапазона t_к;

- вычисляется температура смазки на входе в смазочный слой t₁=t₀+t;

- для заданной марки смазки и температур t₁ и t_к вычисляются значения коэффициентов динамической вязкости ₁ ,_к;

- для заданной марки смазки и температуры t₁ вычисляются значения теплоемкости c₁ и плотности ₁;

- вычисляется значение температурного коэффициента

; (4.2.10)

- в зависимости от заданного признака PRS предусмотрено два основных варианта расчета:

а) PRS=0. Выполняется расчет подшипника при заданной нагрузке F.

При этом определяется положение ротора относительно подшипника, вычисляются потери мощности на трение в гидродинамическом слое NH, межподушечном пространстве NP, дисковые потери ND, минимальная толщина h_min и максимальная температура t_max смазочного слоя;

б) PRS=1. выполняется расчет подшипника для ряда значений относительного эксцентриситета , характеризующего взаимное положение ротора и подшипника. При этом вычисляются гидродинамическая реакция смазочного слоя Р, потери мощности на трение в гидродинамическом слое NH, межподушечном пространстве NP, дисковые потери ND, минимальная толщина h_min и максимальная температура t_max смазочного слоя;

- вычисляются потери мощности на трение в уплотнительных кольцах

NU=, (4.2.11)

суммарные потери мощности на трение N₁=NH+NP+ND+NU;

- расход смазки через зазоры плавающих (PRР= 1) уплотнительных колец

; (4.2.12)

- в случае, когда уплотнительные кольца выполнены фиксированными (PRР= 0) относительно корпуса подшипника, то расход смазки вычисляется по формуле

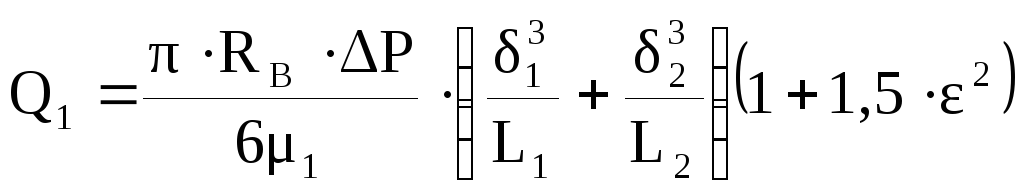; (4.2.13)

В случае, когда предусмотрен расчет узла «подшипник-уплотнение» (рис. 5.) (PRT=1), суммарные потери мощности на трение вычисляются с учетом потерь в торцовом уплотнении N₂=NH+NP+ND+NT+NU.

Расход смазки вычисляется только через одно уплотнительное кольцо

(4.2.14)

или

(4.2.15)

для случая, когда кольцо выполнено фиксированным ( PRР= 0);

Потери мощности на трение в уплотнительном кольце вычисляются по следующей формуле NU=2R³²(L₁/₁);

- из уравнения теплового баланса определяется новое значение перепада температуры смазки в подшипнике

, (4.2.16)

где в зависимости от признака расчета PRT N=N₁ (N₂), Q=Q₁ (Q₂);

- Методом последовательного приближения находится фактическое значение перепада температуры t, соответствующее заданным конструктивным и режимным параметрам подшипника. Решение считается найденным, если значение перепада температуры t и t₁, определяемые в ходе последовательного приближения, не будут отличаться друг от друга более чем на 1%;

- Вычисляется удельный расход смазки

Q*=Q/N;

- В зависимости от заданного признака PRZ в ходе выполнения расчета может производиться уточнение зазоров в уплотнительных кольцах (PRZ=1;

PRT=0) или в одном уплотнительном кольце (PRZ=1; PRT=1).

Рис.5. Схема узла «подшипник-уплотнение»

Уточнение зазоров производится в том случае, если вычисленное значение Q* не соответствует рекомендуемым значениям

Q*=2,510^-53,3310^-5 м³/скВт;

Уточнение зазора производится только для случая расчета подшипника при заданной нагрузке (PRS=0);